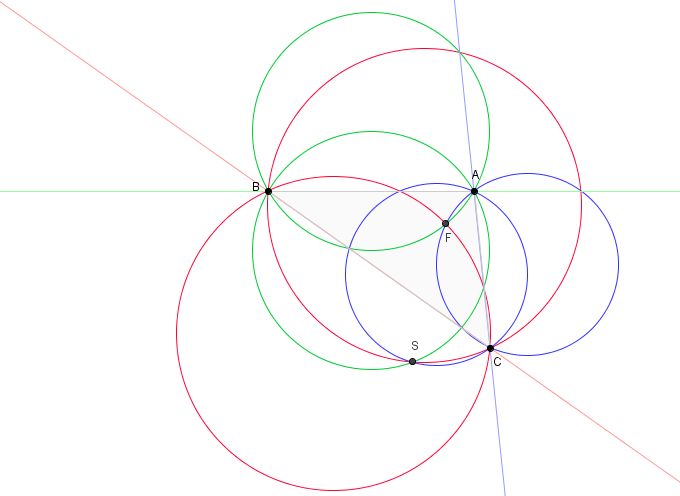
|
Lester Circle
In Euclidean plane geometry, Lester's theorem states that in any scalene triangle, the two Fermat points, the nine-point center, and the circumcenter lie on the same circle. The result is named after June Lester, who published it in 1997, and the circle through these points was called the Lester circle by Clark Kimberling. Lester proved the result by using the properties of complex number In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...s; subsequent authors have given elementary proofs, proofs using vector arithmetic, and computerized proofs. See also * Parry circle * * van Lamoen circle References External links *{{mathworld, id=LesterCircle, title=Lester Circle Theorems about triangles and circles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lester Theorem
Lester is an ancient Anglo-Saxon surname and given name. Notable people and characters with the name include: People Given name * Lester Bangs (1948–1982), American music critic * Lester W. Bentley (1908–1972), American artist from Wisconsin * Lester Bird (1938–2021), second prime minister of Antigua and Barbuda (1994–2004) * Lester Cotton (born 1996), American football player * Lester del Rey (1915–1993), American science fiction author and editor * Lester Flatt (1914–1979), American bluegrass musician * Lester Gillis (1908–1934), better known as Baby Face Nelson, American gangster * Lester Holt (born 1959), American television journalist * Lester Charles King (1907–1989), English geomorphologist * Lester Lanin (1907–2004), American jazz and pop music bandleader * Lester Lockett (1912–2005), American Negro League baseball player * Lester Maddox (1915–2003), governor and lieutenant governor of the U.S. state of Georgia * Lester Patrick (1883–1960), Can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions of parallel lines, and also metrical notions of distance, circles, and angle measurement. The set \mathbb^2 of pairs of real numbers (the real coordinate plane) augmented by appropriate structure often serves as the canonical example. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagorean theorem (Proposition 47), equality of angles and areas, parallelism, the sum of the angles in a triangle, and the three cases in which triangles are "equal" (have the same area), among many other topics. Later, the plane was described in a so-called '' Cartesian coordinate system'', a coordinate system that specifies each point uniquely in a plane by a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalene Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of Euclid's Elements. The names used for modern classification are eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nine-point Center
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers..Encyclopedia of Triangle Centers accessed 2014-10-23. Properties The nine-point center lies on the of its triangle, a ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcenter
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius. Not every polygon has a circumscribed circle. A polygon that does have one is called a cyclic polygon, or sometimes a concyclic polygon because its vertices are concyclic. All triangles, all regular simple polygons, all rectangles, all isosceles trapezoids, and all right kites are cyclic. A related notion is the one of a minimum bounding circle, which is the smallest circle that completely contains the polygon within it, if the circle's center is within the polygon. Every polygon has a unique minimum bounding circle, which may be constructed by a linear time algorithm. Even if a polygon has a circumscribed circle, it may be different from its minimum bounding circle. For example, for an obtuse triangle, the minimum bounding circle has the longest side ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concyclic
In geometry, a set of points are said to be concyclic (or cocyclic) if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic. Bisectors In general the centre ''O'' of a circle on which points ''P'' and ''Q'' lie must be such that ''OP'' and ''OQ'' are equal distances. Therefore ''O'' must lie on the perpendicular bisector of the line segment ''PQ''. For ''n'' distinct points there are ''n''(''n'' − 1)/2 bisectors, and the concyclic condition is that they all meet in a single point, the centre ''O''. Cyclic polygons Triangles The vertices of every triangle fall on a circle. (Because of this, some authors define "concyclic" only in the context of four or more points on a circle.) The circle containing the vertices of a triangle is called the circumscribed circle o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clark Kimberling
Clark Kimberling (born November 7, 1942 in Hinsdale, Illinois) is a mathematician, musician, and composer. He has been a mathematics professor since 1970 at the University of Evansville. His research interests include triangle centers, integer sequences, and hymnology. Kimberling received his PhD in mathematics in 1970 from the Illinois Institute of Technology, under the supervision of Abe Sklar. Since at least 1994, he has maintained a list of triangle centers and their properties. In its current on-line form, the Encyclopedia of Triangle Centers, this list comprises tens of thousands of entries. He has contributed to ''The Hymn'', the journal of the Hymn Society in the United States and Canada; and in the '' Canterbury Dictionary of Hymnology''. Kimberling's golden triangle Robert C. Schoen has defined a "golden triangle" as a triangle with two of its sides in the golden ratio In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parry Circle
In geometry, the Parry point is a special point associated with a plane triangle. It is the triangle center designated X(111) in Clark Kimberling's Encyclopedia of Triangle Centers. The Parry point and Parry circle are named in honor of the English geometer Cyril Parry, who studied them in the early 1990s. Parry circle Let ''ABC'' be a plane triangle. The circle through the centroid and the two isodynamic points of triangle ''ABC'' is called the Parry circle of triangle ''ABC''. The equation of the Parry circle in barycentric coordinates is : \begin & 3(b^2-c^2)(c^2-a^2)(a^2-b^2)(a^2yz+b^2zx+c^2xy) \\ pt& + (x+y+z)\left( \sum_\text b^2c^2(b^2-c^2)(b^2+c^2-2a^2)x\right) =0 \end The center of the Parry circle is also a triangle center. It is the center designated as X(351) in Encyclopedia of Triangle Centers. The trilinear coordinates of the center of the Parry circle are : f(a,b,c) : f(b,c,a) : f(c,a,b) where f(a,b,c) = a(b^2-c^2)(b^2+c^2-2a^2) Parry point The Parry circle an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Lamoen Circle
In Euclidean plane geometry, the van Lamoen circle is a special circle associated with any given triangle T. It contains the circumcenters of the six triangles that are defined inside T by its three medians. Specifically, let A, B, C be the vertices of T, and let G be its centroid (the intersection of its three medians). Let M_a, M_b, and M_c be the midpoints of the sidelines BC, CA, and AB, respectively. It turns out that the circumcenters of the six triangles AGM_c, BGM_c, BGM_a, CGM_a, CGM_b, and AGM_b lie on a common circle, which is the van Lamoen circle of T. History The van Lamoen circle is named after the mathematician Floor van Lamoen https://nl.wikipedia.org/wiki/Floor_van_Lamoen who posed it as a problem in 2000. A proof was provided by Kin Y. Li in 2001, and the editors of the Amer. Math. Monthly in 2002. Properties The center of the van Lamoen circle is point X(1153) in Clark Kimberling's comprehensive list of triangle centers. In 2003, Alexey Myakishev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |