|
Laughlin Wavefunction
In condensed matter physics, the Laughlin wavefunction pp. 210-213 is an ansatz, proposed by Robert Laughlin for the ground state of a two-dimensional electron gas placed in a uniform background magnetic field in the presence of a uniform jellium background when the filling factor (Quantum Hall effect) of the lowest Landau level is \nu=1/n where n is an odd positive integer. It was constructed to explain the observation of the \nu=1/3 fractional quantum Hall effect, and predicted the existence of additional \nu = 1/n states as well as quasiparticle excitations with fractional electric charge e/n, both of which were later experimentally observed. Laughlin received one third of the Nobel Prize in Physics in 1998 for this discovery. Being a trial wavefunction, it is not exact, but qualitatively, it reproduces many features of the exact solution and quantitatively, it has very high overlaps with the exact ground state for small systems. If we ignore the jellium and mutual Coulomb r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with "condensed" phases of matter: systems of many constituents with strong interactions between them. More exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theories to develop mathematical models. The diversity of systems and phenomena available for study makes condensed matter phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
101017 Expectation Value Vs L
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hall Effect
The Hall effect is the production of a voltage difference (the Hall voltage) across an electrical conductor that is transverse to an electric current in the conductor and to an applied magnetic field perpendicular to the current. It was discovered by Edwin Hall in 1879. A Hall effect can also occur across a void or hole in a semiconductor or metal plate, when current is injected via contacts that lie on the boundary or edge of the void or hole, and the charge flows outside the void or hole, in the metal or semiconductor. This Hall effect becomes observable in a perpendicular applied magnetic field across voltage contacts that lie on the boundary of the void on either side of a line connecting the current contacts. It exhibits apparent sign reversal in comparison to the standard "ordinary Hall effect" in the simply connected specimen, and depends only on the current injected from within the void. Superposition may also be realized in the Hall effect: first imagine the standard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Quantum Hall Effect
The fractional quantum Hall effect (FQHE) is a physical phenomenon in which the Hall conductance of 2-dimensional (2D) electrons shows precisely quantized plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations have a fractional elementary charge and possibly also fractional statistics. The 1998 Nobel Prize in Physics was awarded to Robert Laughlin, Horst Störmer, and Daniel Tsui "for their discovery of a new form of quantum fluid with fractionally charged excitations" Laughlin's explanation only applies to fillings \nu = 1/m where m is an odd integer. The microscopic origin of the FQHE is a major research topic in condensed matter physics. Introduction The fractional quantum Hall effect (FQHE) is a collective behavior in a 2D system of electrons. In particular magnetic fields, the electron gas condenses into a remarkable liquid state, which is very delicate, requ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau Level
In quantum mechanics, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete, equidistant energy values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau. Landau quantization is directly responsible for the electronic susceptibility of metals, known as Landau diamagnetism. Under strong magnetic fields, Landau quantization leads to oscillations in electronic properties of materials as a function of the applied magnetic field known as De Haas–Van Alphen and Shubnikov–de Haas effects. Landau quantization is a key ingredient to explain the integer quantum Hall effect. Derivation Consider a system of non-interacting particles with charge and spin confined to an area in the plane ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Common Integrals In Quantum Field Theory
Common integrals in quantum field theory are all variations and generalizations of Gaussian integrals to the complex plane and to multiple dimensions. Other integrals can be approximated by versions of the Gaussian integral. Fourier integrals are also considered. Variations on a simple Gaussian integral Gaussian integral The first integral, with broad application outside of quantum field theory, is the Gaussian integral. G \equiv \int_^ e^\,dx In physics the factor of 1/2 in the argument of the exponential is common. Note: G^2 = \left ( \int_^ e^\,dx \right ) \cdot \left ( \int_^ e^\,dy \right ) = 2\pi \int_^ r e^\,dr = 2\pi \int_^ e^\,dw = 2 \pi. Thus we obtain \int_^ e^\,dx = \sqrt. Slight generalization of the Gaussian integral \int_^ e^\,dx = \sqrt where we have scaled x \to . Integrals of exponents and even powers of ''x'' \int_^ x^2 e^\,dx = -2 \int_^ e^\,dx = -2 \left ( \right ) ^ = \left ( \right ) ^ and \int_^ x^4 e^\,dx = \left ( -2 \right) \left ( -2 \ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
101021 Energy Vs N
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
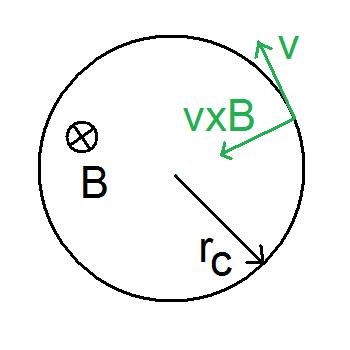
Cyclotron Frequency
Cyclotron resonance describes the interaction of external forces with charged particles experiencing a magnetic field, thus already moving on a circular path. It is named after the cyclotron, a cyclic particle accelerator that utilizes an oscillating electric field tuned to this resonance to add kinetic energy to charged particles. Cyclotron resonance frequency The cyclotron frequency or gyrofrequency is the frequency of a charged particle moving perpendicular to the direction of a uniform magnetic field ''B'' (constant magnitude and direction). Since that motion is always circular,Physics by M. Alonso & E. Finn, Addison Wesley 1996. the cyclotron frequency is given by equality of centripetal force and magnetic Lorentz force :\frac = qBv with the particle mass ''m'', its charge ''q'', velocity ''v'', and the circular path radius ''r'', also called gyroradius. The angular speed of the rotation is then: :\omega = \frac = \frac. Giving the rotational frequency (being the cyclotron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Larmor Radius
The gyroradius (also known as radius of gyration, Larmor radius or cyclotron radius) is the radius of the circular motion of a charged particle in the presence of a uniform magnetic field. In SI units, the non-relativistic gyroradius is given by :r_ = \frac where m is the mass of the particle, v_ is the component of the velocity perpendicular to the direction of the magnetic field, q is the electric charge of the particle, and B is the strength of the magnetic field. The angular frequency of this circular motion is known as the gyrofrequency, or cyclotron frequency, and can be expressed as :\omega_ = \frac in units of radians/second. Variants It is often useful to give the gyrofrequency a sign with the definition :\omega_ = \frac or express it in units of hertz with :f_ = \frac. For electrons, this frequency can be reduced to :f_ = (2.8\times10^\,\mathrm/\mathrm)\times B. In cgs-units the gyroradius :r_ = \frac and the corresponding gyrofrequency :\omega_ = \frac include a factor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel Function
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when the Helmholtz equation is solved in spherical coordinates. Applications of Bessel functions The Bessel function is a generalizat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confluent Hypergeometric Function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity. The term ''confluent'' refers to the merging of singular points of families of differential equations; ''confluere'' is Latin for "to flow together". There are several common standard forms of confluent hypergeometric functions: * Kummer's (confluent hypergeometric) function , introduced by , is a solution to Kummer's differential equation. This is also known as the confluent hypergeometric function of the first kind. There is a different and unrelated Kummer's function bearing the same name. * Tricomi's (confluent hypergeometric) function introduced by , sometimes denoted by , is another solution to Kummer's equation. This is also known as the confluent hypergeometric function of the second kind. * Whittaker functions (for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |