|
Landau Kinetic Equation
The Landau kinetic equation is a transport equation of weakly coupled charged particles performing Coulomb collisions in a plasma. The equation was derived by Lev Landau in 1936 as an alternative to the Boltzmann equation in the case of Coulomb interaction. When used with the Vlasov equation, the equation yields the time evolution for collisional plasma, hence it is considered a staple kinetic model in the theory of collisional plasma. Overview Definition Let f(v, t) be a one-particle Distribution function. The equation reads: \frac = B \frac\left(\int_dw \frac\left(\frac - \frac\right)f(v)f(w)\right) u = v - w The right-hand side of the equation is known as the Landau collision integral (in parallel to the Boltzmann collision integral). B is obtained by integrating over the intermolecular potential U(r): B = \frac\int_0^\infty dr \, r^3 \hat(r)^2 \hat(, k, ) = \int_ dx \, U(, x, ) e^ For many intermolecular potentials (most notably power laws where U(r) \propto \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Coulomb Collision
A Coulomb collision is a binary elastic collision between two charged particles interacting through their own electric field. As with any inverse-square law, the resulting trajectories of the colliding particles is a hyperbolic Keplerian orbit. This type of collision is common in plasmas where the typical kinetic energy of the particles is too large to produce a significant deviation from the initial trajectories of the colliding particles, and the cumulative effect of many collisions is considered instead. Simplified mathematical treatment for plasmas In a plasma, a Coulomb collision rarely results in a large deflection. The cumulative effect of the many small angle collisions, however, is often larger than the effect of the few large angle collisions that occur, so it is instructive to consider the collision dynamics in the limit of small deflections. We can consider an electron of charge -e and mass m_e passing a stationary ion of charge +Ze and much larger mass at a dista ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Coulomb Potential
The electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in an electric field. More precisely, it is the energy per unit charge for a test charge that is so small that the disturbance of the field under consideration is negligible. Furthermore, the motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar quantity denoted by or occasionally , equal to the electric potential energ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Eponymous Equations Of Physics
An eponym is a person, a place, or a thing after whom or which someone or something is, or is believed to be, named. The adjectives which are derived from the word eponym include ''eponymous'' and ''eponymic''. Usage of the word The term ''eponym'' functions in multiple related ways, all based on an explicit relationship between two named things. A person, place, or thing named after a particular person share an eponymous relationship. In this way, Elizabeth I of England is the eponym of the Elizabethan era. When Henry Ford is referred to as "the ''eponymous'' founder of the Ford Motor Company", his surname "Ford" serves as the eponym. The term also refers to the title character of a fictional work (such as Rocky Balboa of the ''Rocky'' film series), as well as to ''self-titled'' works named after their creators (such as the album ''The Doors'' by the band the Doors). Walt Disney created the eponymous Walt Disney Company, with his name similarly extended to theme parks such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Relativistic Speed
Relativistic speed refers to speed at which relativistic effects become significant to the desired accuracy of measurement of the phenomenon being observed. Relativistic effects are those discrepancies between values calculated by models considering and not considering relativity. Related words are velocity, rapidity, and celerity which is proper velocity. Speed is a scalar, being the magnitude of the velocity vector which in relativity is the four-velocity and in three-dimension Euclidean space a three-velocity. Speed is empirically measured as average speed, although current devices in common use can estimate speed over very small intervals and closely approximate instantaneous speed. Non-relativistic discrepancies include cosine error which occurs in speed detection devices when only one scalar component of the three-velocity is measured and the Doppler effect which may affect observations of wavelength and frequency. Relativistic effects are highly non-linear and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Spartak Belyaev
Spartak Timofeyevich Belyaev (October 27, 1923 – January 5, 2017) was a Soviet and Russian theoretical physicist who was awarded a Lomonosov Gold Medal. Biography Belyaev was born on October 27, 1923 in Moscow, Russia. When World War II began, he graduated from high school and by August 1941 enlisted himself into the Army as a volunteer. During that time he participated in various battles in Caucasus and liberation of Poland in 1945. After long years of war, he declined the offer on keeping the career and instead decided to become a physicist by applying to the Moscow State University. Two years later he already got a job there as a researcher at the Atomic Energy Institute which later on was renamed as Kurchatov Institute. He worked there till 1962 and between that year and 1958 also worked at the Niels Bohr Institute in Copenhagen. In 1962 he decided to change his lifestyle a bit; he moved to Siberia and in 1968 was elected as a full member of Russian Academy of Sciences. He w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Gersh Budker
Gersh Itskovich Budker (Герш Ицкович Будкер), also named Andrey Mikhailovich Budker (1 May 1918 – 4 July 1977), was a Soviet physicist, specialized in nuclear physics and accelerator physics. Biography He was elected a Corresponding Member of the Siberian Division of the Soviet Academy of Sciences on 28 March 1958 and was promoted to an ''Academician'' of the Division of Nuclear Physics on 26 June 1964. He is best known for his invention in 1968 of electron cooling, a method of reducing the emittance of particle beams by thermalisation with a co-propagating electron beam. Academician Budker was the founder (in 1959) and first Director of the Budker Institute of Nuclear Physics in Akademgorodok, Russian SFSR. There he lived in the 100-Flat Building. His portrait decorates the famous Round Table Room in the Institute. After his death, the Institute was renamed the Budker Institute for Nuclear Physics in his honor. Budker became one of the founders of Faculty o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Special Relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates: # The laws of physics are invariant (that is, identical) in all inertial frames of reference (that is, frames of reference with no acceleration). # The speed of light in vacuum is the same for all observers, regardless of the motion of the light source or the observer. Origins and significance Special relativity was originally proposed by Albert Einstein in a paper published on 26 September 1905 titled "On the Electrodynamics of Moving Bodies".Albert Einstein (1905)''Zur Elektrodynamik bewegter Körper'', ''Annalen der Physik'' 17: 891; English translatioOn the Electrodynamics of Moving Bodiesby George Barker Jeffery and Wilfrid Perrett (1923); Another English translation On the Electrodynamics of Moving Bodies by Megh Nad Saha (1920). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Inverse-square Law
In science, an inverse-square law is any scientific law stating that a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space. Radar energy expands during both the signal transmission and the reflected return, so the inverse square for both paths means that the radar will receive energy according to the inverse fourth power of the range. To prevent dilution of energy while propagating a signal, certain methods can be used such as a waveguide, which acts like a canal does for water, or how a gun barrel restricts hot gas expansion to one dimension in order to prevent loss of energy transfer to a bullet. Formula In mathematical notation the inverse square law can be expressed as an intensity (I) varying as a function of distance (d) from some centre. The intens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
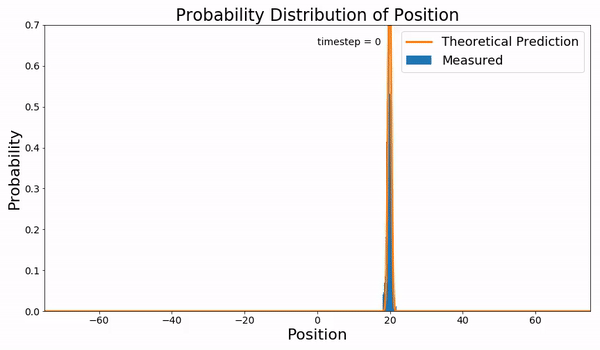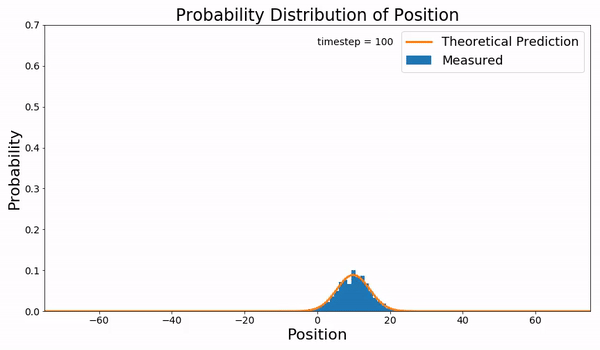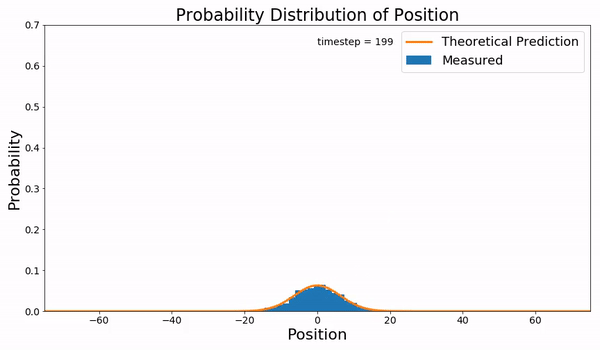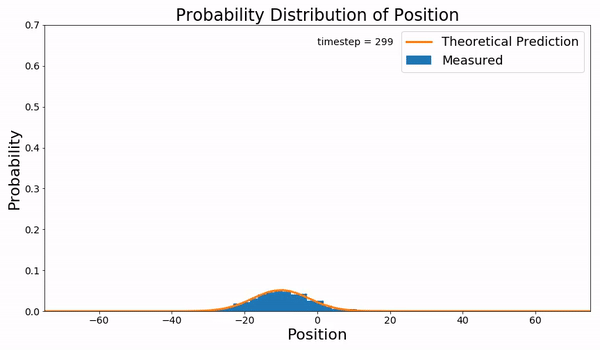 |
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Marshall Rosenbluth
Marshall Nicholas Rosenbluth (5 February 1927 – 28 September 2003) was an American plasma physicist and member of the National Academy of Sciences, and member of the American Philosophical Society. In 1997 he was awarded the National Medal of Science for discoveries in controlled thermonuclear fusion, contributions to plasma physics, and work in computational statistical mechanics. He was also a recipient of the E.O. Lawrence Prize (1964), the Albert Einstein Award (1967), the James Clerk Maxwell Prize for Plasma Physics (1976), the Enrico Fermi Award (1985), and the Hannes Alfvén Prize (2002). Key scientific contributions During his first post-doctoral position at Stanford University (1949–1950), he derived the ''Rosenbluth formula'', which was the basis of the analysis used by Robert Hofstadter in his Nobel prize-winning experimental investigation of electron scattering. Hofstadter refers to this in his 1961 Nobel Lecture: "This behavior can be understood in terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Nikolay Bogolyubov
Nikolay Nikolayevich Bogolyubov (russian: Никола́й Никола́евич Боголю́бов; 21 August 1909 – 13 February 1992), also transliterated as Bogoliubov and Bogolubov, was a Soviet and Russian mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and the theory of dynamical systems; he was the recipient of the 1992 Dirac Medal. Biography Early life (1909–1921) Nikolay Bogolyubov was born on 21 August 1909 in Nizhny Novgorod, Russian Empire to Russian Orthodox Church priest and seminary teacher of theology, psychology and philosophy Nikolay Mikhaylovich Bogolyubov, and Olga Nikolayevna Bogolyubova, a teacher of music. The Bogolyubovs relocated to the village of Velikaya Krucha in the Poltava Governorate (now in Poltava Oblast, Ukraine) in 1919, where the young Nikolay Bogolyubov began to study physics and mathematics. The family soon moved to Kiev in 1921, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
BBGKY Hierarchy
In statistical physics, the BBGKY hierarchy (Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy, sometimes called Bogoliubov hierarchy) is a set of equations describing the dynamics of a system of a large number of interacting particles. The equation for an ''s''-particle distribution function (probability density function) in the BBGKY hierarchy includes the (''s'' + 1)-particle distribution function, thus forming a coupled chain of equations. This formal theoretic result is named after Nikolay Bogolyubov, Max Born, Herbert S. Green, John Gamble Kirkwood, and Jacques Yvon. Formulation The evolution of an ''N''-particle system in absence of quantum fluctuations is given by the Liouville equation for the probability density function f_N = f_N(\mathbf_1 \dots \mathbf_N, \mathbf_1 \dots \mathbf_N, t) in 6''N''-dimensional phase space (3 space and 3 momentum coordinates per particle) : \frac + \sum_^N \frac \frac + \sum_^N \mathbf_i \frac = 0, where \mathbf_i, \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |