|
LOCC
LOCC, or local operations and classical communication, is a method in quantum information theory where a local (product) operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed conditioned on the information received. Mathematical properties The formal definition of the set of LOCC operations is complicated due to the fact that later local operations depend in general on all the previous classical communication and due to the unbounded number of communication rounds. For any finite number r\geq1 one can define \operatorname_r, the set of LOCC operations that can be achieved with r rounds of classical communication. The set becomes strictly larger whenever r is increased and care has to be taken to define the limit of infinitely many rounds. In particular, the set LOCC is not topologically closed, that is there are quantum operations that can be approximat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Entanglement
Quantum entanglement is the phenomenon where the quantum state of each Subatomic particle, particle in a group cannot be described independently of the state of the others, even when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical physics and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurement#Quantum mechanics, Measurements of physical properties such as position (vector), position, momentum, Spin (physics), spin, and polarization (waves), polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Teleportation
Quantum teleportation is a technique for transferring quantum information from a sender at one location to a receiver some distance away. While teleportation is commonly portrayed in science fiction as a means to transfer physical objects from one location to the next, quantum teleportation only transfers quantum information. The sender does not have to know the particular quantum state being transferred. Moreover, the location of the recipient can be unknown, but to complete the quantum teleportation, classical information needs to be sent from sender to receiver. Because classical information needs to be sent, quantum teleportation cannot occur faster than the speed of light. One of the first scientific articles to investigate quantum teleportation is "Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels" published by Charles H. Bennett (physicist), C. H. Bennett, Gilles Brassard, G. Brassard, Claude Crépeau, C. Crépeau, Richard Jozsa, R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separable State
In quantum mechanics, separable states are multipartite quantum states that can be written as a convex combination of product states. Product states are multipartite quantum states that can be written as a tensor product of states in each space. The physical intuition behind these definitions is that product states have no correlation between the different degrees of freedom, while separable states might have correlations, but all such correlations can be explained as due to a classical random variable, as opposed to being due to entanglement. In the special case of pure states the definition simplifies: a pure state is separable if and only if it is a product state. A state is said to be entangled if it is not separable. In general, determining if a state is separable is not straightforward and the problem is classed as NP-hard. Separability of bipartite systems Consider first composite states with two degrees of freedom, referred to as ''bipartite states''. By a postulate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unextendible Product Basis
In quantum mechanics Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ..., an unextendible product basis is a set of orthogonal, non- entangled state vectors for a multipartite system, with the property that local operations and classical communication are insufficient to distinguish one member of the set from the others. Because these states are product states and yet local measurements cannot tell them apart, they are sometimes said to exhibit "nonlocality without entanglement". They provide examples of non-entangled states that pass the Peres–Horodecki criterion for entanglement. See also * Bound entanglement References {{Quantum-stub Quantum information theory Quantum states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Operation
In quantum mechanics, a quantum operation (also known as quantum dynamical map or quantum process) is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan. The quantum operation formalism describes not only unitary time evolution or symmetry transformations of isolated systems, but also the effects of measurement and transient interactions with an environment. In the context of quantum computation, a quantum operation is called a quantum channel. Note that some authors use the term "quantum operation" to refer specifically to completely positive (CP) and non-trace-increasing maps on the space of density matrices, and the term "quantum channel" to refer to the subset of those that are strictly trace-preserving. Quantum operations are formulated in terms of the density operator description of a quantum mechanic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
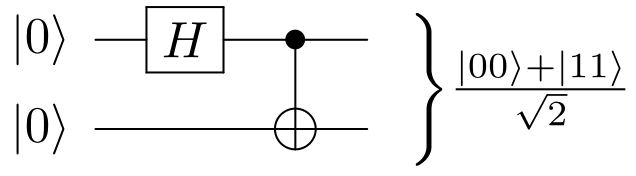
Bell State
In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particles being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding of Bell's states is useful in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Qubit
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical system, one of the simplest quantum systems displaying the peculiarity of quantum mechanics. Examples include the spin of the electron in which the two levels can be taken as spin up and spin down; or the polarization of a single photon in which the two spin states (left-handed and the right-handed circular polarization) can also be measured as horizontal and vertical linear polarization. In a classical system, a bit would have to be in one state or the other. However, quantum mechanics allows the qubit to be in a coherent superposition of multiple states simultaneously, a property that is fundamental to quantum mechanics and quantum computing. Etymology The coining of the term ''qubit'' is attributed to Benjamin Schumacher. In the acknow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Nonlocality
In theoretical physics, quantum nonlocality refers to the phenomenon by which the measurement statistics of a multipartite quantum system do not allow an interpretation with local realism. Quantum nonlocality has been experimentally verified under a variety of physical assumptions. Quantum nonlocality does not allow for faster-than-light communication, and hence is compatible with special relativity and its universal speed limit of objects. Thus, quantum theory is local in the strict sense defined by special relativity and, as such, the term "quantum nonlocality" is sometimes considered a misnomer. Still, it prompts many of the foundational discussions concerning quantum theory. History Einstein, Podolsky and Rosen In the 1935 EPR paper, Albert Einstein, Boris Podolsky and Nathan Rosen described "two spatially separated particles which have both perfectly correlated positions and momenta" as a direct consequence of quantum theory. They intended to use the classical princip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Information Theory
Quantum information is the information of the state of a quantum system. It is the basic entity of study in quantum information theory, and can be manipulated using quantum information processing techniques. Quantum information refers to both the technical definition in terms of Von Neumann entropy and the general computational term. It is an interdisciplinary field that involves quantum mechanics, computer science, information theory, philosophy and cryptography among other fields. Its study is also relevant to disciplines such as cognitive science, psychology and neuroscience. Its main focus is in extracting information from matter at the microscopic scale. Observation in science is one of the most important ways of acquiring information and measurement is required in order to quantify the observation, making this crucial to the scientific method. In quantum mechanics, due to the uncertainty principle, non-commuting observables cannot be precisely measured simultaneously, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |