|
L10a140 Link
In the knot theory, mathematical theory of knots, L10a140 is the name in thThistlethwaite link tableof a link (knot theory), link of three loops, which has ten crossings between the loops when presented in its simplest visual form. It is of interest because it is presumably the simplest link which possesses the Brunnian link, Brunnian property — a link of connected components that, when one component is removed, becomes entirely unconnected — other than the six-crossing Borromean rings. In other words, no two loops are Hopf link, directly linked with each other, but all three are collectively interlinked, so removing any loop frees the other two. In the image in the infobox at right, the red loop is not interlinked with either the blue or the yellow loops, and if the red loop is removed, then the blue and yellow loops can also be disentangled from each other without cutting either one. According to work by Slavik V. Jablan, the L10a140 link can be seen as the second in an inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In the mathematical field of topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, Unknot, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3 (in topology, a circle is not bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of descr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constitut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
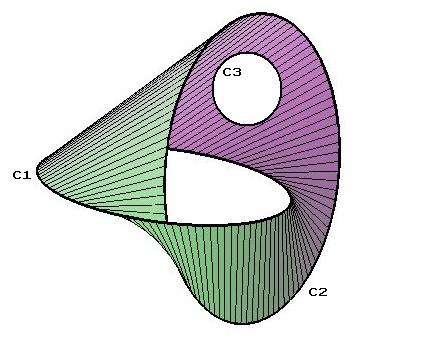
Brunnian Link
In knot theory, a branch of topology, a Brunnian link is a nontrivial link that becomes a set of trivial unlinked circles if any one component is removed. In other words, cutting any loop frees all the other loops (so that no two loops can be directly linked). The name ''Brunnian'' is after Hermann Brunn. Brunn's 1892 article ''Über Verkettung'' included examples of such links. Examples The best-known and simplest possible Brunnian link is the Borromean rings, a link of three unknots. However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: Image:Brunnian-3-not-Borromean.svg, 12-crossing link. Image:Three-triang-18crossings-Brunnian.svg, 18-crossing link. Image:Three-interlaced-squares-Brunnian-24crossings.svg, 24-crossing link. The simplest Brunnian link other than the 6-cros ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Colin Adams (mathematician)
Colin Conrad Adams (born October 13, 1956) is a mathematician primarily working in the areas of hyperbolic 3-manifolds and knot theory. His book, ''The Knot Book'', has been praised for its accessible approach to advanced topics in knot theory. He is currently Francis Christopher Oakley Third Century Professor of Mathematics at Williams College, where he has been since 1985. He writes "Mathematically Bent", a column of math for the ''Mathematical Intelligencer''. His nephew is popular American singer Still Woozy. Academic career Adams received a B.Sc. from MIT in 1978 and a Ph.D. in mathematics from the University of Wisconsin–Madison in 1983. His dissertation was entitled "Hyperbolic Structures on Link Complements" and supervised by James Cannon. In 2012 he became a fellow of the American Mathematical Society. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borromean Rings
In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing. The Borromean rings are named after the Italian House of Borromeo, who used the circular form of these rings as a coat of arms, but designs based on the Borromean rings have been used in many cultures, including by the Norsemen and in Japan. They have been used in Christian symbolism as a sign of the Trinity, and in modern commerce as the logo of Ballantine beer, giving them the alternative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dror Bar-Natan
Dror Bar-Natan ( he, דרוֹר בָר-נָתָן; born January 30, 1966) is a professor at the University of Toronto Department of Mathematics, Canada. His main research interests include knot theory, finite type invariants, and Khovanov homology. Education Bar-Natan earned his B.Sc. in mathematics at Tel Aviv University in 1984. After performing his military service as a teacher, he went to study at Princeton University in 1987. He obtained his Ph.D. in mathematics from Princeton in 1991, under the direction of physicist Edward Witten. Professorship After holding a Benjamin Peirce Assistant Professorship at Harvard University for four years from 1991–95, he returned to Israel, and became Associate Professor at the Hebrew University of Jerusalem. He moved to the University of Toronto in 2002, and was promoted to Full Professor in 2006. Personal life Bar-Natan holds US, Israeli, and Canadian citizenship, and currently resides in Canada. Bar-Natan originally refused to take th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hopf Link
In mathematical knot theory, the Hopf link is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once, and is named after Heinz Hopf. Geometric realization A concrete model consists of two unit circles in perpendicular planes, each passing through the center of the other.. See in particulap. 77 This model minimizes the ropelength of the link and until 2002 the Hopf link was the only link whose ropelength was known. The convex hull of these two circles forms a shape called an oloid. Properties Depending on the relative orientations of the two components the linking number of the Hopf link is ±1. The Hopf link is a (2,2)-torus link with the braid word :\sigma_1^2.\, The knot complement of the Hopf link is R × ''S''1 × ''S''1, the cylinder over a torus. This space has a locally Euclidean geometry, so the Hopf link is not a hyperbolic link. The knot group of the Hopf link (the fund ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander–Conway Polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial. Definition Let ''K'' be a knot in the 3-sphere. Let ''X'' be the infinite cyclic cover of the knot complement of ''K''. This covering can be obtained by cutting the knot complement along a Seifert surface of ''K'' and gluing together infinitely many copies of the resulting manifold with boundary in a cyclic manner. There is a covering transformation ''t'' acting on ''X''. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jones Polynomial
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable t^ with integer coefficients. Definition by the bracket Suppose we have an oriented link L, given as a knot diagram. We will define the Jones polynomial, V(L), using Louis Kauffman's bracket polynomial, which we denote by \langle~\rangle. Here the bracket polynomial is a Laurent polynomial in the variable A with integer coefficients. First, we define the auxiliary polynomial (also known as the normalized bracket polynomial) :X(L) = (-A^3)^\langle L \rangle, where w(L) denotes the writhe of L in its given diagram. The writhe of a diagram is the number of positive crossings (L_ in the figure below) minus the number of negative crossings (L_). The writhe is not a knot invariant. X(L) is a knot invariant since it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whitehead Link
In knot theory, the Whitehead link, named for J. H. C. Whitehead, is one of the most basic links. It can be drawn as an alternating link with five crossings, from the overlay of a circle and a figure-eight shaped loop. Structure A common way of describing this knot is formed by overlaying a figure-eight shaped loop with another circular loop surrounding the crossing of the figure-eight. The above-below relation between these two unknots is then set as an alternating link, with the consecutive crossings on each loop alternating between under and over. This drawing has five crossings, one of which is the self-crossing of the figure-eight curve, which does not count towards the linking number. Because the remaining crossings have equal numbers of under and over crossings on each loop, its linking number is 0. It is not isotopic to the unlink, but it is link homotopic to the unlink. Although this construction of the knot treats its two loops differently from each other, the two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
HOMFLY Polynomial
In the mathematical field of knot theory, the HOMFLY polynomial or HOMFLYPT polynomial, sometimes called the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables ''m'' and ''l''. A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial, which is computed from a diagram of the knot and can be shown to be an invariant of the knot, i.e. diagrams representing the same knot have the same polynomial. The converse may not be true. The HOMFLY polynomial is one such invariant and it generalizes two polynomials previously discovered, the Alexander polynomial and the Jones polynomial, both of which can be obtained by appropriate substitutions from HOMFLY. The HOMFLY polynomial is also a quantum invariant. The name ''HOMFLY'' combines the initials of its co-discoverers: Jim Hoste, Adrian Ocneanu, Kenn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kauffman Polynomial
In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman. It is initially defined on a link diagram as :F(K)(a,z)=a^L(K)\,, where w(K) is the writhe of the link diagram and L(K) is a polynomial in ''a'' and ''z'' defined on link diagrams by the following properties: *L(O) = 1 (O is the unknot). *L(s_r)=aL(s), \qquad L(s_\ell)=a^L(s). *''L'' is unchanged under type II and III Reidemeister moves. Here s is a strand and s_r (resp. s_\ell) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move). Additionally ''L'' must satisfy Kauffman's skein relation: : The pictures represent the ''L'' polynomial of the diagrams which differ inside a disc as shown but are identical outside. Kauffman showed that ''L'' exists and is a regular isotopy invariant of unoriented links. It follows easily that ''F'' is an ambient isotopy invariant of oriented links. The Jones polynomial is a special case of the Kauf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Whitehead Link")