|
List Of Mathematical Topics In Classical Mechanics
{{Short description, none This is a list of mathematical topics in classical mechanics, by Wikipedia page. See also list of variational topics, correspondence principle. Newtonian physics *Newton's laws of motion *Inertia, * Kinematics, rigid body *Momentum, kinetic energy *Parallelogram of force * Circular motion **Rotational speed **Angular speed *Angular momentum **torque **angular acceleration **moment of inertia ***parallel axes rule *** perpendicular axes rule ***stretch rule **centripetal force, centrifugal force, Reactive centrifugal force **Laplace–Runge–Lenz vector *Euler's disk *elastic potential energy *Mechanical equilibrium *D'Alembert's principle *Degrees of freedom (physics and chemistry) *Frame of reference *Inertial frame of reference *Galilean transformation *Principle of relativity Conservation laws *Conservation of momentum **Conservation of linear momentum **Conservation of angular momentum *Conservation of energy **Potential energy *Conservative force ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Variational Topics
{{Short description, none This is a list of variational topics in from mathematics and physics. See calculus of variations for a general introduction. * Action (physics) * Averaged Lagrangian * Brachistochrone curve * Calculus of variations * Catenoid * Cycloid * Dirichlet principle * Euler–Lagrange equation cf. Action (physics) * Fermat's principle * Functional (mathematics) * Functional derivative * Functional integral * Geodesic * Isoperimetry * Lagrangian * Lagrangian mechanics * Legendre transformation * Luke's variational principle * Minimal surface * Morse theory * Noether's theorem * Path integral formulation * Plateau's problem * Prime geodesic * Principle of least action * Soap bubble * Soap film * Tautochrone curve Variations Variation or Variations may refer to: Science and mathematics * Variation (astronomy), any perturbation of the mean motion or orbit of a planet or satellite, particularly of the moon * Genetic variation, the difference in DNA among individuals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
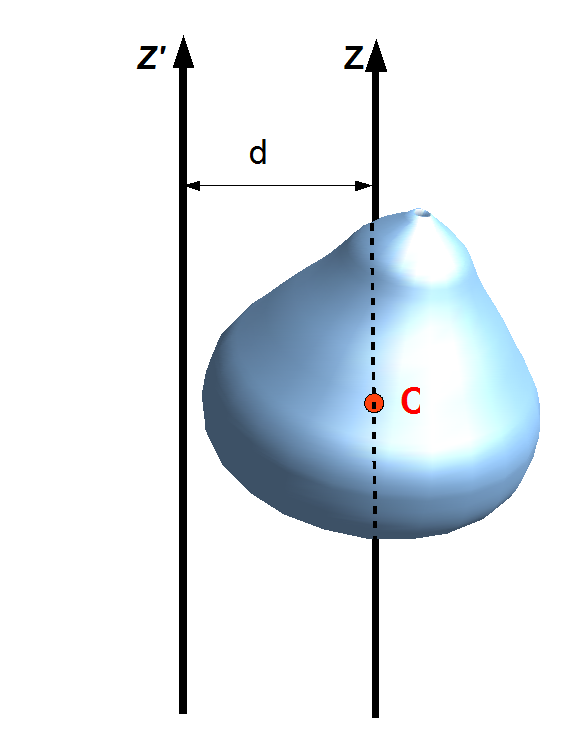
Parallel Axes Rule
The parallel axis theorem, also known as Huygens–Steiner theorem, or just as Steiner's theorem, named after Christiaan Huygens and Jakob Steiner, can be used to determine the moment of inertia or the second moment of area of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's center of gravity and the perpendicular distance between the axes. Mass moment of inertia Suppose a body of mass is rotated about an axis passing through the body's center of mass. The body has a moment of inertia with respect to this axis. The parallel axis theorem states that if the body is made to rotate instead about a new axis , which is parallel to the first axis and displaced from it by a distance , then the moment of inertia with respect to the new axis is related to by : I = I_\mathrm + md^2. Explicitly, is the perpendicular distance between the axes and . The parallel axis theorem can be applied with the stretch rule and perpe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertial Frame Of Reference
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. It is a frame in which an isolated physical object — an object with zero net force acting on it — is perceived to move with a constant velocity (it might be a zero velocity) or, equivalently, it is a frame of reference in which Newton's first law of motion holds. All inertial frames are in a state of constant, rectilinear motion with respect to one another; in other words, an accelerometer moving with any of them would detect zero acceleration. It has been observed that celestial objects which are far away from other objects and which are in uniform motion with respect to the cosmic microwave background radiation maintain such uniform motion. Measurements in one inertial frame can be converted to measurements in another by a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frame Of Reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathematically (with numerical coordinate values) and physically (signaled by conventional markers). For ''n'' dimensions, reference points are sufficient to fully define a reference frame. Using rectangular Cartesian coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the ''n'' coordinate axes. In Einsteinian relativity, reference frames are used to specify the relationship between a moving observer and the phenomenon under observation. In this context, the term often becomes observational frame of reference (or observational reference frame), which implies that the observer is at rest in the frame, although not necessarily located at its origin. A rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (physics And Chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space. The location of a particle in three-dimensional space requires three Coordinate system, position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is Deterministic system, deterministic (where the state at one instant uniquely determines its past and future position and velocity as a function of time) such a system has six degrees of freedom. If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D'Alembert's Principle
D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert. D'Alembert's principle generalizes the principle of virtual work from static to dynamical systems by introducing ''forces of inertia'' which, when added to the applied forces in a system, result in ''dynamic equilibrium''. The principle does not apply for irreversible displacements, such as sliding friction, and more general specification of the irreversibility is required. D'Alembert's principle is more general than Hamilton's principle as it is not restricted to holonomic constraints that depend only on coordinates and time but not on velocities. Statement of the principle The principle states that the sum of the differences between the forces acting on a system of massive particles and the time derivatives of the momenta of the system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero. In addition to defining mechanical equilibrium in terms of force, there are many alternative definitions for mechanical equilibrium which are all mathematically equivalent. In terms of momentum, a system is in equilibrium if the momentum of its parts is all constant. In terms of velocity, the system is in equilibrium if velocity is constant. In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero. More generally in conservative systems, equilibrium is established at a point in configuration space where the gradient of the potential energy with respect to the generalized coordinates is zero. If a particle in equilibrium has zero velocity, that particle is in static equilibriu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Potential Energy
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed, stretched or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials. (Note however, the work done by a stretched rubber band is not an example of elastic energy. It is an example of entropic elasticity.) The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into other forms of energy, such as kinetic energy and sound energy, when the object is allowed to return to its original shape (reformation) by its elasticity. U = \frac 1 2 k\, \Delta x^2 The essence of elasticity is reversibility. Forces applied to an elastic material transfer energy into the material whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Disk
Euler's Disk, invented between 1987 and 1990 by Joseph Bendik, is a trademark for a scientific educational toy. It is used to illustrate and study the dynamic system of a spinning and rolling disk on a flat or curved surface. It has been the subject of several scientific papers. Discovery Joseph Bendik first noted the interesting motion of the spinning disk while working at Hughes Aircraft (Carlsbad Research Center) after spinning a heavy polishing chuck on his desk at lunch one day. The apparatus is a dramatic visualization of energy exchanges in three different, tightly coupled processes. As the disk gradually decreases its azimuthal rotation, there is also a decrease in amplitude and increase in the frequency of the disk's axial precession. The evolution of the disk's axial precession is easily visualized in a slow motion video by looking at the side of the disk following a single point marked on the disk. The evolution of the rotation of the disk is easily visualized in sl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace–Runge–Lenz Vector
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be '' conserved''. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems. The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schr� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reactive Centrifugal Force
In classical mechanics, a reactive centrifugal force forms part of an action–reaction pair with a centripetal force. In accordance with Newton's first law of motion, an object moves in a straight line in the absence of a net force acting on the object. A curved path may however ensue when such a force acts on it; this force is often called a centripetal force, as it is directed toward the center of curvature of the path. Then in accordance with Newton's third law of motion, there will also be an equal and opposite force exerted by the object on some other object, such as a constraint that forces the path to be curved, and this reaction force, the subject of this article, is sometimes called a reactive centrifugal force, as it is directed in the opposite direction of the centripetal force. Unlike the inertial force or fictitious force known as centrifugal force, which always exists in addition to the reactive force in the rotating frame of reference, the reactive force is a r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centrifugal Force (fictitious)
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parallel to the axis of rotation and passing through the coordinate system's origin. If the axis of rotation passes through the coordinate system's origin, the centrifugal force is directed radially outwards from that axis. The magnitude of centrifugal force ''F'' on an object of mass ''m'' at the distance ''r'' from the origin of a frame of reference rotating with angular velocity is: F = m\omega^2 r The concept of centrifugal force can be applied in rotating devices, such as centrifuges, centrifugal pumps, centrifugal governors, and centrifugal clutches, and in centrifugal railways, planetary orbits and banked curves, when they are analyzed in a rotating coordinate system. Confusingly, the term has sometimes also been used for the reac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |