|
List Of Geodesic-geocoding Systems
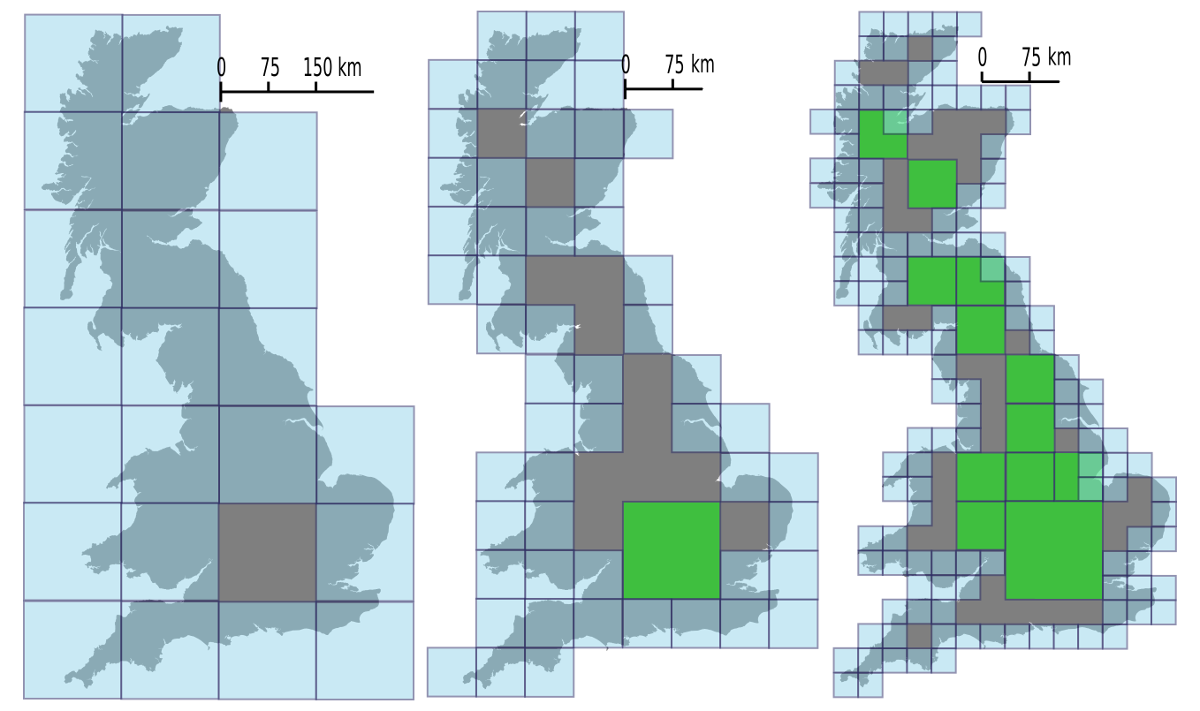
A discrete global grid (DGG) is a mosaic that covers the entire Earth's surface. Mathematically it is a space partitioning: it consists of a set of non-empty regions that form a partition of the Earth's surface. In a usual grid-modeling strategy, to simplify position calculations, each region is represented by a point, abstracting the grid as a set of region-points. Each region or region-point in the grid is called a cell. When each cell of a grid is subject to a recursive partition, resulting in a "series of discrete global grids with progressively finer resolution", forming a hierarchical grid, it is called a hierarchical DGG (sometimes "global hierarchical tessellation" or "DGG system"). Discrete global grids are used as the geometric basis for the building of geospatial data structures. Each cell is related with data objects or values, or (in the hierarchical case) may be associated with other cells. DGGs have been proposed for use in a wide range of geospatial applicat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include '' regular tilings'' with regular polygonal tiles all of the same shape, and '' semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An '' aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern (an aperiodic set of prototiles). A '' tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodetic Datum
A geodetic datum or geodetic system (also: geodetic reference datum, geodetic reference system, or geodetic reference frame, or terrestrial reference frame) is a global datum reference or reference frame for unambiguously representing the position of locations on Earth by means of either geodetic coordinates (and related vertical coordinates) or geocentric coordinates. DatumsThe plural is not "data" in this case are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a horizontal position, across the Earth's surface, in latitude and longitude or another related coordinate system. A ''vertical datum'' is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). A three-dimensional datum enables the expression of both horizontal and vertical position components in a unified form. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Military Grid Reference System
The Military Grid Reference System (MGRS) Datums, Ellipsoids, Grids, and Grid Reference Systems is the geocoordinate standard used by NATO militaries for locating points on Earth. The MGRS is derived from the Universal Transverse Mercator coordinate system, Universal Transverse Mercator (UTM) grid system and the Universal polar stereographic coordinate system, Universal Polar Stereographic (UPS) grid system, but uses a different labeling convention. The MGRS is used as geocode for the entire Earth. It’s also referred as 10-digit coordinates. An example of an ''MGRS coordinate'', or ''grid reference'', would be [21_18_34.0_N_157_55_0.7_W_&language=en 4QFJ12345678], which consists of three parts: * 4Q (grid zone designator, GZD) * FJ (the 100,000-meter square identifier) * 1234 5678 (numerical location; Easting and nort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Transverse Mercator
The Universal Transverse Mercator (UTM) is a map projection system for assigning coordinates to locations on the surface of the Earth. Like the traditional method of latitude and longitude, it is a horizontal position representation, which means it ignores altitude and treats the earth surface as a perfect ellipsoid. However, it differs from global latitude/longitude in that it divides earth into 60 zones and projects each to the plane as a basis for its coordinates. Specifying a location means specifying the zone and the ''x'', ''y'' coordinate in that plane. The projection from spheroid to a UTM zone is some parameterization of the transverse Mercator projection. The parameters vary by nation or region or mapping system. Most zones in UTM span 6 degrees of longitude, and each has a designated central meridian. The scale factor at the central meridian is specified to be 0.9996 of true scale for most UTM systems in use. History The National Oceanic and Atmospheric Administratio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voronoi Diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation. The Voronoi diagram is named after mathematician Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi cells are also known as Thiessen polygons, after Alfred H. Thiessen. Voronoi diagrams have practical and theoretical applications in many fields, mainly in science and technology, but also in visual art. Simplest case In the simplest case, shown in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Tilings By Convex Regular Polygons
Euclidean Plane (mathematics), plane Tessellation, tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Johannes Kepler, Kepler in his (Latin language, Latin: ''The Harmony of the World'', 1619). Notation of Euclidean tilings Euclidean tilings are usually named after Cundy & Rollett’s notation. This notation represents (i) the number of vertices, (ii) the number of polygons around each vertex (arranged clockwise) and (iii) the number of sides to each of those polygons. For example: 36; 36; 34.6, tells us there are 3 vertices with 2 different vertex types, so this tiling would be classed as a ‘3-uniform (2-vertex types)’ tiling. Broken down, 36; 36 (both of different transitivity class), or (36)2, tells us that there are 2 vertices (denoted by the superscript 2), each with 6 equilateral 3-sided polygons (triangles). With a final vertex 34.6, 4 more contiguous equilateral triangles and a single re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unstructured Grid
An unstructured grid or irregular grid is a tessellation of a part of the Euclidean plane or Euclidean space by simple shapes, such as triangles or tetrahedra, in an irregular pattern. Grids of this type may be used in finite element analysis when the input to be analyzed has an irregular shape. Unlike structured grids, unstructured grids require a list of the connectivity which specifies the way a given set of vertices make up individual elements (see graph (data structure) In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics. A graph data structure consists of a finite (and possibly mut ...). Ruppert's algorithm is often used to convert an irregularly shaped polygon into an unstructured grid of triangles. In addition to triangles and tetrahedra, other commonly used elements in finite element simulation include quadrilateral (4-noded) and hex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
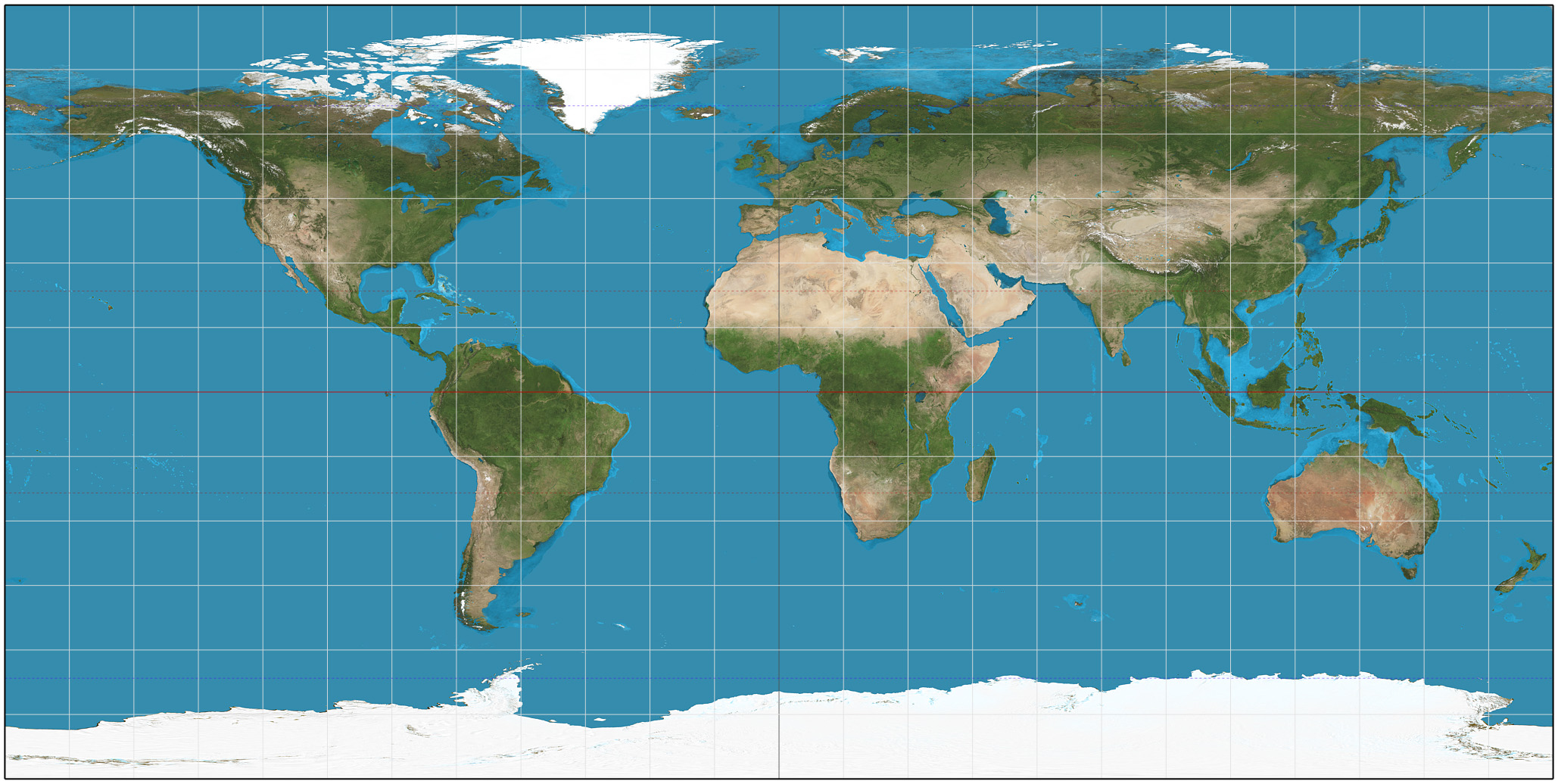
Geographic Coordinate System
A geographic coordinate system (GCS) is a spherical coordinate system, spherical or geodetic coordinates, geodetic coordinate system for measuring and communicating position (geometry), positions directly on Earth as latitude and longitude. It is the simplest, oldest, and most widely used type of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface. A full GCS specification, such as those listed in the EPSG Geodetic Parameter Dataset, EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location. History The invention of a geographic coordinate system is generally credited to Eratosthenes of Cy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Reference System
A spatial reference system (SRS) or coordinate reference system (CRS) is a framework used to precisely measure locations on the surface of Earth as coordinates. It is thus the application of the abstract mathematics of coordinate systems and analytic geometry to geographic space. A particular SRS specification (for example, "Universal Transverse Mercator WGS 84 Zone 16N") comprises a choice of Earth ellipsoid, Geodetic datum, horizontal datum, map projection (except in the geographic coordinate system), origin point, and unit of measure. Thousands of coordinate systems have been specified for use around the world or in specific regions and for various purposes, necessitating geographic coordinate conversion, transformations between different SRS. Although they date to the Hellenistic period, spatial reference systems are now a crucial basis for the sciences and technologies of Geoinformatics, including cartography, geographic information systems, surveying, remote sensing, and civ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
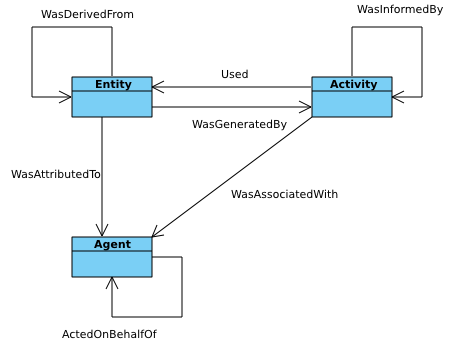
Data Lineage
Data lineage refers to the process of tracking how data is generated, transformed, transmitted and used across a system over time. It documents data's origins, transformations and movements, providing detailed visibility into its life cycle. This process simplifies the identification of errors in data analytics workflows, by enabling users to trace issues back to their root causes. Data lineage facilitates the ability to replay specific segments or inputs of the dataflow. This can be used in debugging or regenerating lost outputs. In database systems, this concept is closely related to data provenance, which involves maintaining records of inputs, entities, systems and processes that influence data. Data provenance provides a historical record of data origins and transformations. It supports forensic activities such as data-dependency analysis, error/compromise detection, recovery, auditing and compliance analysis: "''Lineage'' is a simple type of ''why provenance''."De, Soumyarup ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polyhedra
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is identified by its Schläfli symbol of the form , where ''n'' is the number of sides of each face and ''m'' the number of faces meeting at each vertex. There are 5 finite convex regular polyhedra (the Platonic solids), and four regular star polyhedra (the Kepler–Poinsot polyhedra), making nine regular polyhedra in all. In addition, there are five regular compounds of the regular polyhedra. The regular polyhedra There are five convex regular polyhedra, known as the Platonic solids; four regular star polyhedra, the Kepler–Poinsot polyhedra; and five regular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |