|
Linear Forms In Logarithms
In transcendental number theory, a mathematical discipline, Baker's theorem gives a lower bound for the absolute value of linear combinations of logarithms of algebraic numbers. Nearly fifteen years earlier, Alexander Gelfond had considered the problem with only integer coefficients to be of "extraordinarily great significance". The result, proved by , subsumed many earlier results in transcendental number theory. Baker used this to prove the transcendence of many numbers, to derive effective bounds for the solutions of some Diophantine equations, and to solve the class number problem of finding all imaginary quadratic fields with class number 1. History To simplify notation, let \mathbb be the set of logarithms to the base ''e'' of nonzero algebraic numbers, that is \mathbb = \left \, where \Complex denotes the set of complex numbers and \overline denotes the algebraic numbers (the algebraic closure of the rational numbers \Q). Using this notation, several results in transcendent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Number Theory
Transcendental number theory is a branch of number theory that investigates transcendental numbers (numbers that are not solutions of any polynomial equation with rational coefficients), in both qualitative and quantitative ways. Transcendence The fundamental theorem of algebra tells us that if we have a non-constant polynomial with rational coefficients (or equivalently, by clearing denominators, with integer coefficients) then that polynomial will have a root in the complex numbers. That is, for any non-constant polynomial P with rational coefficients there will be a complex number \alpha such that P(\alpha)=0. Transcendence theory is concerned with the converse question: given a complex number \alpha, is there a polynomial P with rational coefficients such that P(\alpha)=0? If no such polynomial exists then the number is called transcendental. More generally the theory deals with algebraic independence of numbers. A set of numbers is called algebraically independen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Height Function
A height function is a function that quantifies the complexity of mathematical objects. In Diophantine geometry, height functions quantify the size of solutions to Diophantine equations and are typically functions from a set of points on algebraic varieties (or a set of algebraic varieties) to the real numbers. For instance, the ''classical'' or ''naive height'' over the rational numbers is typically defined to be the maximum of the numerators and denominators of the coordinates (e.g. for the coordinates ), but in a logarithmic scale. Significance Height functions allow mathematicians to count objects, such as rational points, that are otherwise infinite in quantity. For instance, the set of rational numbers of naive height (the maximum of the numerator and denominator when expressed in lowest terms) below any given constant is finite despite the set of rational numbers being infinite. In this sense, height functions can be used to prove asymptotic results such as Baker's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-adic
In number theory, given a prime number , the -adic numbers form an extension of the rational numbers which is distinct from the real numbers, though with some similar properties; -adic numbers can be written in a form similar to (possibly infinite) decimals, but with digits based on a prime number rather than ten, and extending to the left rather than to the right. For example, comparing the expansion of the rational number \tfrac15 in base vs. the -adic expansion, \begin \tfrac15 &= 0.01210121\ldots \ (\text 3) &&= 0\cdot 3^0 + 0\cdot 3^ + 1\cdot 3^ + 2\cdot 3^ + \cdots \\ mu\tfrac15 &= \dots 121012102 \ \ (\text) &&= \cdots + 2\cdot 3^3 + 1 \cdot 3^2 + 0\cdot3^1 + 2 \cdot 3^0. \end Formally, given a prime number , a -adic number can be defined as a series s=\sum_^\infty a_i p^i = a_k p^k + a_ p^ + a_ p^ + \cdots where is an integer (possibly negative), and each a_i is an integer such that 0\le a_i < p. A -adic integer is a -adic number such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Polynomial
In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial x^3 + 3 x^2 y + z^7 is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function. An algebraic form, or simply form, is a function defined by a homogeneous polynomial.However, as some authors do not make a clear distinction between a polynomial and its associated function, the terms ''homogeneous polynomial'' and ''form'' are sometimes considered as synonymous. A binary form is a form in two variables. A ''form'' is also a function defined on a vector space, which may be expressed as a homogeneous function of the coordinates over any basis. A polynomial of degree 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Independence
In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non- trivial polynomial equation with coefficients in K. In particular, a one element set \ is algebraically independent over K if and only if \alpha is transcendental over K. In general, all the elements of an algebraically independent set S over K are by necessity transcendental over K, and over all of the field extensions over K generated by the remaining elements of S. Example The real numbers \sqrt and 2\pi+1 are transcendental numbers: they are not the roots of any nontrivial polynomial whose coefficients are rational numbers. Thus, the sets \ and \ are both algebraically independent over the rational numbers. However, the set \ is ''not'' algebraically independent over the rational numbers \mathbb, because the nontrivial polynomial :P(x,y)=2x^2-y+1 is zero when x=\sqrt and y=2\pi+1. Algebraic independence of known constants Although an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
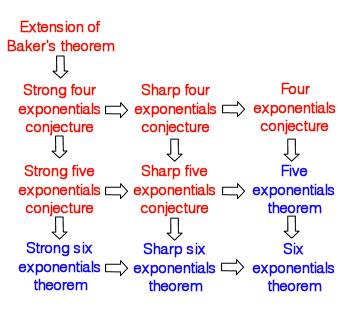
Four Exponentials Conjecture
In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function. Statement If ''x''1, ''x''2 and ''y''1, ''y''2 are two pairs of complex numbers, with each pair being linearly independent over the rational numbers, then at least one of the following four numbers is transcendental: :e^, e^, e^, e^. An alternative way of stating the conjecture in terms of logarithms is the following. For 1 ≤ ''i'', ''j'' ≤ 2 let λ''ij'' be complex numbers such that exp(λ''ij'') are all algebraic. Suppose λ11 and λ12 are linearly independent over the rational numbers, and λ11 and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Six Exponentials Theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of six exponentials. Statement : If x_1, x_2, x_3 are three complex numbers that are linearly independent over the rational numbers, and y_1, y_2 are two complex numbers that are also linearly independent over the rational numbers, then at least one of the following numbers is transcendental: e^, e^, e^, e^, e^, e^. The theorem can be stated in terms of logarithms by introducing the set ''L'' of logarithms of algebraic numbers: :\mathcal=\. The theorem then says that if \lambda_ are elements of ''L'' for i = 1,2, j = 1,2,3 such that \lambda_, \lambda_, \lambda_ are linearly independent over the rational numbers, and λ11 and λ21 are also linearly independent over the rational numbers, then the matrix :M=\begin\lambda_&\lambda_&\lambda_ \\ \lambda_&\lambda_&\lambda_\end ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schanuel's Conjecture
In mathematics, specifically transcendental number theory, Schanuel's conjecture is a conjecture about the transcendence degree of certain field extensions of the rational numbers \mathbb, which would establish the transcendence of a large class of numbers, for which this is currently unknown. It is due to Stephen Schanuel and was published by Serge Lang in 1966. Statement Schanuel's conjecture can be given as follows: Consequences Schanuel's conjecture, if proven, would generalize most known results in transcendental number theory and establish a large class of numbers transcendental. Special cases of Schanuel's conjecture include: Lindemann-Weierstrass theorem Considering Schanuel's conjecture for only n=1 gives that for nonzero complex numbers z, at least one of the numbers z and e^z must be transcendental. This was proved by Ferdinand von Lindemann in 1882. If the numbers z_1,...,z_n are taken to be all algebraic and linearly independent over \mathbb Q then the e^,.. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vandermonde Matrix
In linear algebra, a Vandermonde matrix, named after Alexandre-Théophile Vandermonde, is a matrix with the terms of a geometric progression in each row: an (m + 1) \times (n + 1) matrix :V = V(x_0, x_1, \cdots, x_m) = \begin 1 & x_0 & x_0^2 & \dots & x_0^n\\ 1 & x_1 & x_1^2 & \dots & x_1^n\\ 1 & x_2 & x_2^2 & \dots & x_2^n\\ \vdots & \vdots & \vdots & \ddots &\vdots \\ 1 & x_m & x_m^2 & \dots & x_m^n \end with entries V_ = x_i^j , the ''j''th power of the number x_i, for all zero-based indices i and j . Some authors define the Vandermonde matrix as the transpose of the above matrix. The determinant of a square Vandermonde matrix (when n=m) is called a Vandermonde determinant or Vandermonde polynomial. Its value is: :\det(V) = \prod_ (x_j - x_i). This is non-zero if and only if all x_i are distinct (no two are equal), making the Vandermonde matrix invertible. Applications The polynomial interpolation problem is to find a polynomial p(x) = a_0 + a_1 x + a_2 x^2 + \dots + a_n x^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Siegel's Lemma
In mathematics, specifically in transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used what would be translated from German as Dirichlet's Drawers principle, which is widely known as the Pigeonhole principle. Carl Ludwig Siegel published his lemma in 1929. It is a pure existence theorem for a system of linear equations. Siegel's lemma has been refined in recent years to produce sharper bounds on the estimates given by the lemma. Statement Suppose we are given a system of ''M'' linear equations in ''N'' unknowns such that ''N'' > ''M'', say :a_ X_1 + \cdots+ a_ X_N = 0 :\cdots :a_ X_1 +\cdots+ a_ X_N = 0 where the coefficients are integers, not all 0, and bounded by ''B''. The system then has a solution :(X_1, X_2, \dots, X_N) with the ''X''s all integers, not all 0, and boun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vandermonde Determinant
In algebra, the Vandermonde polynomial of an ordered set of ''n'' variables X_1,\dots, X_n, named after Alexandre-Théophile Vandermonde, is the polynomial: :V_n = \prod_ (X_j-X_i). (Some sources use the opposite order (X_i-X_j), which changes the sign \binom times: thus in some dimensions the two formulas agree in sign, while in others they have opposite signs.) It is also called the Vandermonde determinant, as it is the determinant of the Vandermonde matrix. The value depends on the order of the terms: it is an alternating polynomial, not a symmetric polynomial. Alternating The defining property of the Vandermonde polynomial is that it is ''alternating'' in the entries, meaning that permuting the X_i by an odd permutation changes the sign, while permuting them by an even permutation does not change the value of the polynomial – in fact, it is the basic alternating polynomial, as will be made precise below. It thus depends on the order, and is zero if two entries are equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Auxiliary Function
In mathematics, auxiliary functions are an important construction in transcendental number theory. They are functions that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high order at some point. Definition Auxiliary functions are not a rigorously defined kind of function, rather they are functions which are either explicitly constructed or at least shown to exist and which provide a contradiction to some assumed hypothesis, or otherwise prove the result in question. Creating a function during the course of a proof in order to prove the result is not a technique exclusive to transcendence theory, but the term "auxiliary function" usually refers to the functions created in this area. Explicit functions Liouville's transcendence criterion Because of the naming convention mentioned above, auxiliary functions can be dated back to their source simply by looking at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |