|
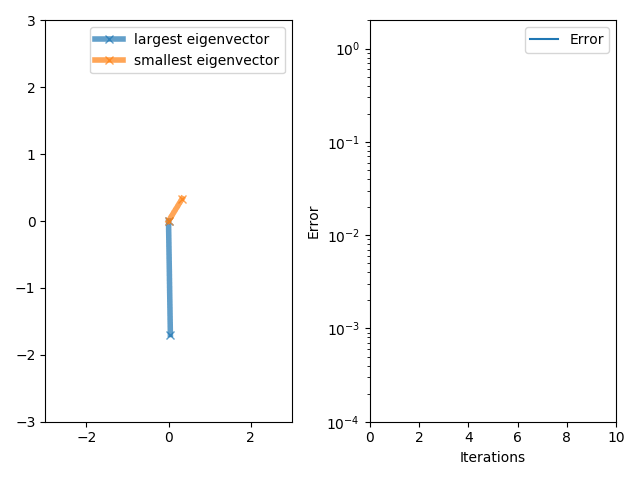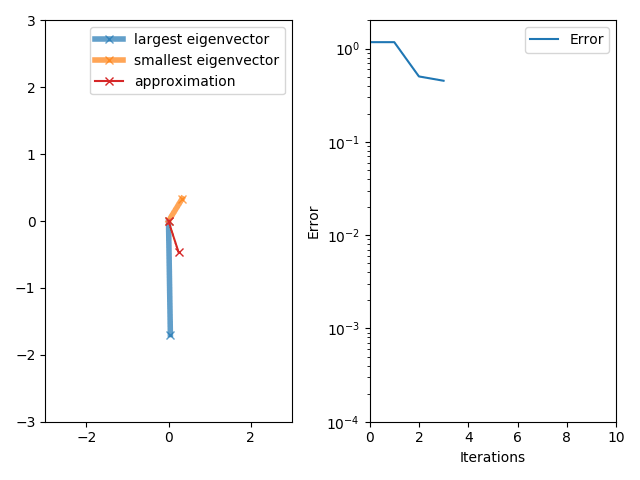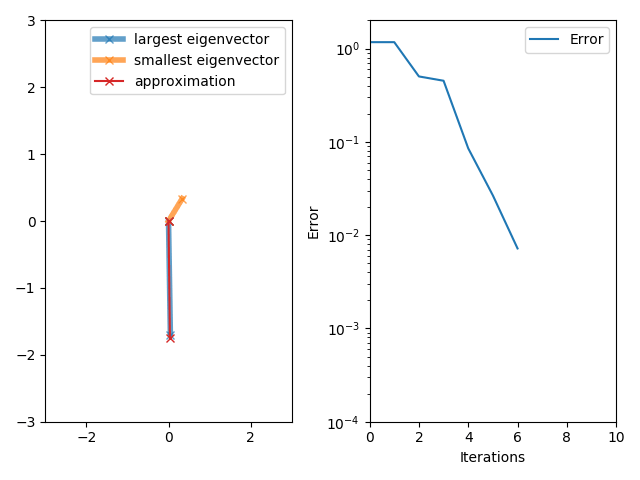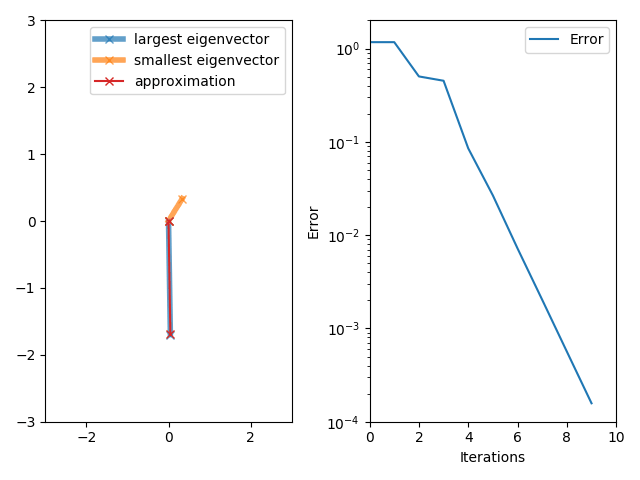
Lanczos Algorithm
The Lanczos algorithm is an iterative method devised by Cornelius Lanczos that is an adaptation of power iteration, power methods to find the m "most useful" (tending towards extreme highest/lowest) eigenvalues and eigenvectors of an n \times n Hermitian matrix, where m is often but not necessarily much smaller than n . Although computationally efficient in principle, the method as initially formulated was not useful, due to its Numerical stability, numerical instability. In 1970, Ojalvo and Newman showed how to make the method numerically stable and applied it to the solution of very large engineering structures subjected to dynamic loading. This was achieved using a method for purifying the Lanczos vectors (i.e. by repeatedly reorthogonalizing each newly generated vector with all previously generated ones) to any degree of accuracy, which when not performed, produced a series of vectors that were highly contaminated by those associated with the lowest natural frequencies. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Method
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''i''-th approximation (called an "iterate") is derived from the previous ones. A specific implementation with Algorithm#Termination, termination criteria for a given iterative method like gradient descent, hill climbing, Newton's method, or Quasi-Newton method, quasi-Newton methods like Broyden–Fletcher–Goldfarb–Shanno algorithm, BFGS, is an algorithm of an iterative method or a method of successive approximation. An iterative method is called ''Convergent series, convergent'' if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Method
In mathematics, power iteration (also known as the power method) is an eigenvalue algorithm: given a diagonalizable matrix A, the algorithm will produce a number \lambda, which is the greatest (in absolute value) eigenvalue of A, and a nonzero vector v, which is a corresponding eigenvector of \lambda, that is, Av = \lambda v. The algorithm is also known as the Von Mises iteration. Richard von Mises and H. Pollaczek-Geiringer, ''Praktische Verfahren der Gleichungsauflösung'', ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 9, 152-164 (1929). Power iteration is a very simple algorithm, but it may converge slowly. The most time-consuming operation of the algorithm is the multiplication of matrix A by a vector, so it is effective for a very large sparse matrix with appropriate implementation. The speed of convergence is like (\lambda_2 / \lambda_1)^k where k is the number of iterations (see a later section). In words, convergence is exponential with base being the spect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hessenberg Matrix
In linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal. They are named after Karl Hessenberg. A Hessenberg decomposition is a matrix decomposition of a matrix A into a unitary matrix P and a Hessenberg matrix H such that PHP^*=A where P^* denotes the conjugate transpose. Definitions Upper Hessenberg matrix A square n \times n matrix A is said to be in upper Hessenberg form or to be an upper Hessenberg matrix if a_=0 for all i,j with i > j+1. An upper Hessenberg matrix is called unreduced if all subdiagonal entries are nonzero, i.e. if a_ \neq 0 for all i \in \. Lower Hessenberg matrix A square n \times n matrix A is said to be in lower Hessenberg form or to be a lower Hessenberg matrix if its transpose is an upper Hessenberg matrix or equivalently if a_=0 for al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Polynomials
In mathematics, an orthogonal polynomial sequence is a family of polynomials such that any two different polynomials in the sequence are orthogonal In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ... to each other under some inner product. The most widely used orthogonal polynomials are the classical orthogonal polynomials, consisting of the Hermite polynomials, the Laguerre polynomials and the Jacobi polynomials. The Gegenbauer polynomials form the most important class of Jacobi polynomials; they include the Chebyshev polynomials, and the Legendre polynomials as special cases. These are frequently given by the Rodrigues' formula. The field of orthogonal polynomials developed in the late 19th century from a study of continued fractions by Pafnuty Chebyshev, P. L. Chebyshev and wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arnoldi Iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of an iterative method. Arnoldi finds an approximation to the eigenvalues and eigenvectors of general (possibly non- Hermitian) matrices by constructing an orthonormal basis of the Krylov subspace, which makes it particularly useful when dealing with large sparse matrices. The Arnoldi method belongs to a class of linear algebra algorithms that give a partial result after a small number of iterations, in contrast to so-called ''direct methods'' which must complete to give any useful results (see for example, Householder transformation). The partial result in this case being the first few vectors of the basis the algorithm is building. When applied to Hermitian matrices it reduces to the Lanczos algorithm. The Arnoldi iteration was invented by W. E. Arnoldi in 1951. Krylov subspaces and the power iteration An intuitive method for finding the largest (in absolute value) ei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
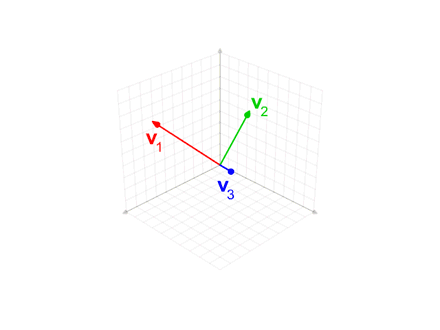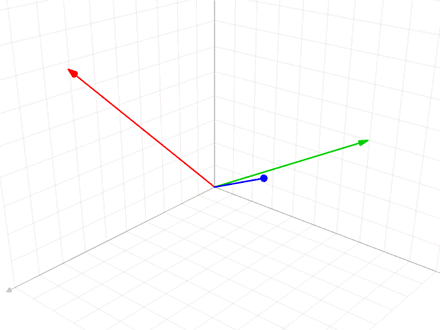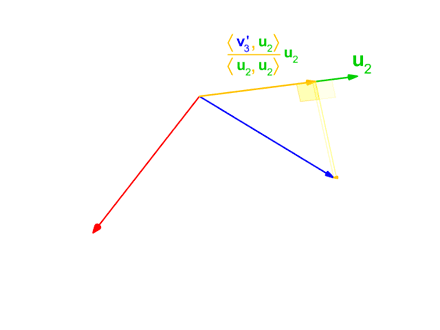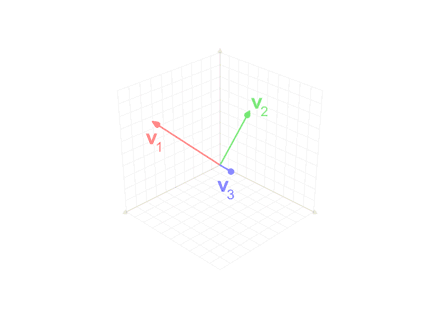
Gram–Schmidt Process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other. By technical definition, it is a method of constructing an orthonormal basis from a set of vector (geometry), vectors in an inner product space, most commonly the Euclidean space \mathbb^n equipped with the standard inner product. The Gram–Schmidt process takes a finite set, finite, linearly independent set of vectors S = \ for and generates an orthogonal set S' = \ that spans the same k-dimensional subspace of \mathbb^n as S. The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition. The application of the Gram–Schmidt process to the column vectors of a full column rank (linear algebra), rank mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ill-conditioned
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem: given f(x) = y, one is solving for ''x,'' and thus the condition number of the (local) inverse must be used. The condition number is derived from the theory of propagation of uncertainty, and is formally defined as the value of the asymptotic worst-case relative change in output for a relative change in input. The "function" is the solution of a problem and the "arguments" are the data in the problem. The condition number is frequently applied to questions in linear algebra, in which case the derivative is straightforward but the error could be in many different directions, and is thus computed from the geometry of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Krylov Subspace
In linear algebra, the order-''r'' Krylov subspace generated by an ''n''-by-''n'' matrix ''A'' and a vector ''b'' of dimension ''n'' is the linear subspace spanned by the images of ''b'' under the first ''r'' powers of ''A'' (starting from A^0=I), that is, :\mathcal_r(A,b) = \operatorname \, \. Background The concept is named after Russian applied mathematician and naval engineer Alexei Krylov, who published a paper about the concept in 1931. Properties * \mathcal_r(A,b), A\,\mathcal_r(A,b)\subset \mathcal_(A,b). * Let r_0 = \operatorname \operatorname \, \. Then \ are linearly independent unless r>r_0, \mathcal_r(A,b) \subset \mathcal_(A,b) for all r, and \operatorname \mathcal_(A,b) = r_0. So r_0 is the maximal dimension of the Krylov subspaces \mathcal_r(A,b). * The maximal dimension satisfies r_0\leq 1 + \operatorname A and r_0 \leq n. * Consider \dim \operatorname \, \ = \deg\,p(A), where p(A) is the minimal polynomial of A. We have r_0\leq \deg\,p(A). Moreover, for an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synchronization (computer Science)
In computer science, synchronization is the task of coordinating multiple processes to join up or handshake at a certain point, in order to reach an agreement or commit to a certain sequence of action. Motivation The need for synchronization does not arise merely in multi-processor systems but for any kind of concurrent processes; even in single processor systems. Mentioned below are some of the main needs for synchronization: '' Forks and Joins:'' When a job arrives at a fork point, it is split into N sub-jobs which are then serviced by n tasks. After being serviced, each sub-job waits until all other sub-jobs are done processing. Then, they are joined again and leave the system. Thus, parallel programming requires synchronization as all the parallel processes wait for several other processes to occur. '' Producer-Consumer:'' In a producer-consumer relationship, the consumer process is dependent on the producer process until the necessary data has been produced. ''Exclusiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Householder Transformation
In linear algebra, a Householder transformation (also known as a Householder reflection or elementary reflector) is a linear transformation that describes a reflection (mathematics), reflection about a plane (mathematics), plane or hyperplane containing the origin. The Householder transformation was used in a 1958 paper by Alston Scott Householder. Definition Operator and transformation The Householder Operator (mathematics), operator may be defined over any finite-dimensional inner product space V with inner product \langle \cdot, \cdot \rangle and unit vector u\in V as : H_u(x) := x - 2\,\langle x,u \rangle\,u\,. It is also common to choose a non-unit vector q \in V, and normalize it directly in the Householder operator's expression: :H_q \left ( x \right ) = x - 2\, \frac\, q \,. Such an operator is Linear operator, linear and self-adjoint. If V=\mathbb^n, note that the reflection hyperplane can be defined by its ''normal vector'', a unit vector \vec v\in V (a vector wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lossy Compression
In information technology, lossy compression or irreversible compression is the class of data compression methods that uses inexact approximations and partial data discarding to represent the content. These techniques are used to reduce data size for storing, handling, and transmitting content. Higher degrees of approximation create coarser images as more details are removed. This is opposed to lossless data compression (reversible data compression) which does not degrade the data. The amount of data reduction possible using lossy compression is much higher than using lossless techniques. Well-designed lossy compression technology often reduces file sizes significantly before degradation is noticed by the end-user. Even when noticeable by the user, further data reduction may be desirable (e.g., for real-time communication or to reduce transmission times or storage needs). The most widely used lossy compression algorithm is the discrete cosine transform (DCT), first published by N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |