|
Kittell Graph
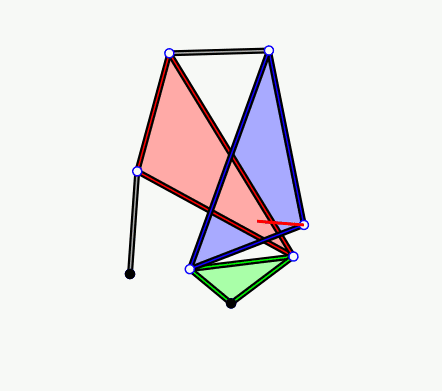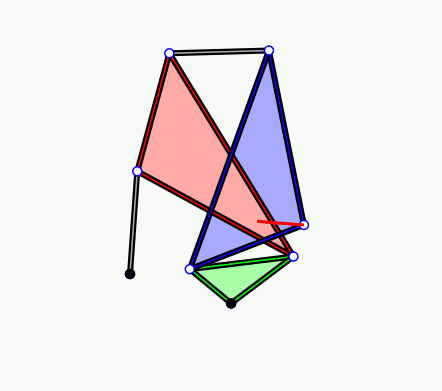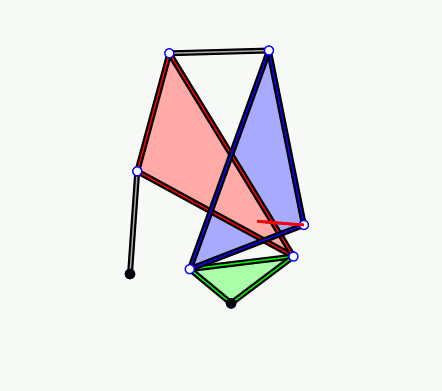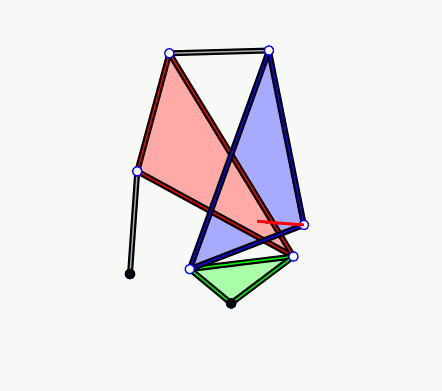
In the mathematical field of graph theory, the Kittell graph is a planar graph with 23 vertices and 63 edges. Its unique planar embedding has 42 triangular faces. The Kittell graph is named after Irving Kittell, who used it as a counterexample to Alfred Kempe's flawed proof of the four-color theorem In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions shar .... Simpler counterexamples include the Errera graph and Poussin graph (both published earlier than Kittell) and the Fritsch graph and Soifer graph. References Individual graphs Planar graphs {{graph-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Planar Graph
In graph theory, a planar graph is a graph (discrete mathematics), graph that can be graph embedding, embedded in the plane (geometry), plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph, or a planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points. Every graph that can be drawn on a plane can be drawn on the sphere as well, and vice versa, by means of stereographic projection. Plane graphs can be encoded by combinatorial maps or rotation systems. An equivalence class of topologically equivalent drawings on the sphere, usually with addit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Alfred Kempe
Sir Alfred Bray Kempe FRS (6 July 1849 – 21 April 1922) was a mathematician best known for his work on linkages and the four colour theorem. Biography Kempe was the son of the Rector of St James's Church, Piccadilly, the Rev. John Edward Kempe. Among his brothers were Sir John Arrow Kempe and Harry Robert Kempe. He was educated at St Paul's School, London and then studied at Trinity College, Cambridge, where Arthur Cayley was one of his teachers. He graduated BA (22nd wrangler) in 1872. Despite his interest in mathematics he became a barrister, specialising in the ecclesiastical law. He was knighted in 1913, the same year he became the Chancellor for the Diocese of London. He was also Chancellor of the dioceses of Newcastle, Southwell, St Albans, Peterborough, Chichester, and Chelmsford. He received the honorary degree DCL from the University of Durham and he was elected a Bencher of the Inner Temple in 1909. In 1876 he published his article ''On a General Met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Four-color Theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions share a common boundary of non-zero length (i.e., not merely a corner where three or more regions meet). It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain. The theorem is a stronger version of the five color theorem, which can be shown using a significantly simpler argument. Although the weaker five color theorem was proven already in the 1800s, the four color theorem resisted until 1976 when it was proven by Kenneth Appel and Wolfgang Haken in a computer-aided proof. This came after many false proofs and mistak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bulletin Of The American Mathematical Society
The ''Bulletin of the American Mathematical Society'' is a quarterly mathematical journal published by the American Mathematical Society. Scope It publishes surveys on contemporary research topics, written at a level accessible to non-experts. It also publishes, by invitation only, book reviews and short ''Mathematical Perspectives'' articles. History It began as the ''Bulletin of the New York Mathematical Society'' and underwent a name change when the society became national. The Bulletin's function has changed over the years; its original function was to serve as a research journal for its members. Indexing The Bulletin is indexed in Mathematical Reviews, Science Citation Index, ISI Alerting Services, CompuMath Citation Index, and Current Contents/Physical, Chemical & Earth Sciences. See also *'' Journal of the American Mathematical Society'' *'' Memoirs of the American Mathematical Society'' *'' Notices of the American Mathematical Society'' *'' Proceedings of the Ame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Errera Graph
In the mathematics, mathematical field of graph theory, the Errera graph is a graph with 17 vertex (graph theory), vertices and 45 edge (graph theory), edges. Alfred Errera published it in 1921 as a counterexample to Alfred Kempe, Kempe's erroneous proof of the four color theorem; it was named after Errera by . Properties The Errera graph is Planar graph, planar and has chromatic number 4, chromatic index 6, radius (graph theory), radius 3, diameter (graph theory), diameter 4 and girth (graph theory), girth 3. All its vertices are of degree 5 or 6 and it is a 5-k-vertex-connected graph, vertex-connected graph and a 5-k-edge-connected graph, edge-connected graph. The Errera graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 20, the group of symmetries of a decagon, including both rotations and reflections. The characteristic polynomial of the Errera graph is -(x^2-2 x-5) (x^2+x-1)^2 (x^3-4 x^2-9 x+10) (x^4+2 x^3-7 x^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Poussin Graph
In graph theory, the Poussin graph is a planar graph with 15 vertices and 39 edges. It is named after Charles Jean de la Vallée-Poussin. History In 1879, Alfred Kempe published a proof of the four color theorem, one of the big conjectures in graph theory. While the theorem is true, Kempe's proof is incorrect. Percy John Heawood illustrated it in 1890 with a counter-example, and de la Vallée-Poussin reached the same conclusion in 1896 with the Poussin graph. Kempe's (incorrect) proof is based on alternating chains, and as those chains prove useful in graph theory mathematicians remain interested in such counterexamples. More were found later: first, the Errera graph in 1921, then the Kittell graph in 1935, with 23 vertices, and finally two minimal counter-examples (the Soifer graph in 1997 and the Fritsch graph in 1998, both of order 9).Gethner, E. and Springer, W. M. II. « How False Is Kempe's Proof of the Four-Color Theorem? » Congr. Numer. 164, 159–175, 2003. Refer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fritsch Graph
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid. The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle. The dual polyhedron of the triaugmented triangular prism is an associahedron, a polyhedron with four quadrilate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Soifer Graph
Soifer is a surname. Notable people with the surname include: *Alexander Soifer Alexander Soifer is a Russian-born American mathematician and mathematics author. Soifer obtained his Ph.D. in 1973 and has been a professor of mathematics at the University of Colorado since 1979. He was visiting fellow at Princeton University ... (born 1948), Russian-born American mathematician and mathematics author * Aviam Soifer (born 1948), American legal scholar and academic administrator See also * Sofer (other) {{surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Individual Graphs
An individual is one that exists as a distinct entity. Individuality (or self-hood) is the state or quality of living as an individual; particularly (in the case of humans) as a person unique from other people and possessing one's own needs or goals, rights and responsibilities. The concept of an individual features in many fields, including biology, law, and philosophy. Every individual contributes significantly to the growth of a civilization. Society is a multifaceted concept that is shaped and influenced by a wide range of different things, including human behaviors, attitudes, and ideas. The culture, morals, and beliefs of others as well as the general direction and trajectory of the society can all be influenced and shaped by an individual's activities. Etymology From the 15th century and earlier (and also today within the fields of statistics and metaphysics) ''individual'' meant " indivisible", typically describing any numerically singular thing, but sometimes meani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |