|
K0 (other)
K0 may refer to: * Spectral class K0, a star spectral class * the 1965 first model of the Honda CB450 motorbike * the Grothendieck group in abstract algebra * the Lateral_earth_pressure#At_rest_pressure, Lateral earth pressure at rest * the neutral kaon, a strange meson with no charge in nuclear physics * K0 may refer to Khinchin's constant * K0 the Null graph#Order-zero graph, order-zero graph {{Letter-NumberCombDisambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Class
In astronomy, stellar classification is the classification of stars based on their spectral characteristics. Electromagnetic radiation from the star is analyzed by splitting it with a prism or diffraction grating into a spectrum exhibiting the rainbow of colors interspersed with spectral lines. Each line indicates a particular chemical element or molecule, with the line strength indicating the abundance of that element. The strengths of the different spectral lines vary mainly due to the temperature of the photosphere, although in some cases there are true abundance differences. The ''spectral class'' of a star is a short code primarily summarizing the ionization state, giving an objective measure of the photosphere's temperature. Most stars are currently classified under the Morgan–Keenan (MK) system using the letters ''O'', ''B'', ''A'', ''F'', ''G'', ''K'', and ''M'', a sequence from the hottest (''O'' type) to the coolest (''M'' type). Each letter class is then subdivided ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honda CB450
The Honda CB450 is a standard motorcycle made by Honda from 1965 to 1974 with a 180° DOHC straight-twin engine. Producing 45 bhp (some 100 bhp/ litre), it was Honda's first "big" motorcycle, though it did not succeed in its goal of competing directly against the larger Triumphs, Nortons, and Harley-Davidsons in the North American market at the time. As a result, Honda tried again, leading to the development of the four cylinder Honda CB750 that marked a turning point for Honda and beginning of the "superbike" era of motorcycles. Design The CB450 had a distinctive chrome-sided fuel tank, and shared Honda's 'family' styling found elsewhere on the S90 and CD175. Early models were known as the 'Black Bomber', ''Motor Cycle'', 17 February 1966. Colour centrespread official Honda CB450 UK advertisement. "''Meet the big black bomber...''" "£360.0.0" Accessed 2013-08-22 or 'Dragon', but in Canada the K1 model was marketed as the 'Hellcat'. The four-speed K0 model was updated in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grothendieck Group
In mathematics, the Grothendieck group, or group of differences, of a commutative monoid is a certain abelian group. This abelian group is constructed from in the most universal way, in the sense that any abelian group containing a homomorphic image of will also contain a homomorphic image of the Grothendieck group of . The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation. Grothendieck group of a commutative monoid Motivation Given a commutative monoid , "the most general" abelian group that arises from is to be constructed by introducing inverse elements to all elements of . Such an abelian group always exists; it is called the Grothendieck group of . It is character ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lateral Earth Pressure
Lateral earth pressure is the pressure that soil exerts in the horizontal direction. The lateral earth pressure is important because it affects the consolidation behavior and strength of the soil and because it is considered in the design of geotechnical engineering structures such as retaining walls, basements, tunnels, deep foundations and braced excavations. The earth pressure problem dates from the beginning of the 18th century, when Gautier listed five areas requiring research, one of which was the dimensions of gravity-retaining walls needed to hold back soil. However, the first major contribution to the field of earth pressures was made several decades later by Coulomb, who considered a rigid mass of soil sliding upon a shear surface. Rankine extended earth pressure theory by deriving a solution for a complete soil mass in a state of failure, as compared with Coulomb's solution which had considered a soil mass bounded by a single failure surface. Originally, the Rankine's the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kaon
KAON (Karlsruhe ontology) is an ontology infrastructure developed by the University of Karlsruhe and the Research Center for Information Technologies in Karlsruhe. Its first incarnation was developed in 2002 and supported an enhanced version of RDF ontologies. Several tools like the graphical ontology editor OIModeler or the KAON Server were based on KAON. There are ontology learning companion tools which take non-annotated natural language text as input: TextToOnto (KAON-based) and Text2Onto (KAON2-based). Text2Onto is based on the Probabilistic Ontology Model (POM). In 2005, the first version of KAON2 was released, offering fast reasoning support for OWL ontologies. KAON2 is not backward-compatible with KAON. KAON2 is developed as a joint effort of the Information Process Engineering (IPE) at the Research Center for Information Technologies (FZI), the Institute of Applied Informatics and Formal Description Methods (AIFB) at the University of Karlsruhe, and the Information Ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Physics
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter. Nuclear physics should not be confused with atomic physics, which studies the atom as a whole, including its electrons. Discoveries in nuclear physics have led to applications in many fields. This includes nuclear power, nuclear weapons, nuclear medicine and magnetic resonance imaging, industrial and agricultural isotopes, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology. Such applications are studied in the field of nuclear engineering. Particle physics evolved out of nuclear physics and the two fields are typically taught in close association. Nuclear astrophysics, the application of nuclear physics to astrophysics, is crucial in explaining the inner workings of stars and the origin of the chemical elements. History The history of nuclear physics as a discipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
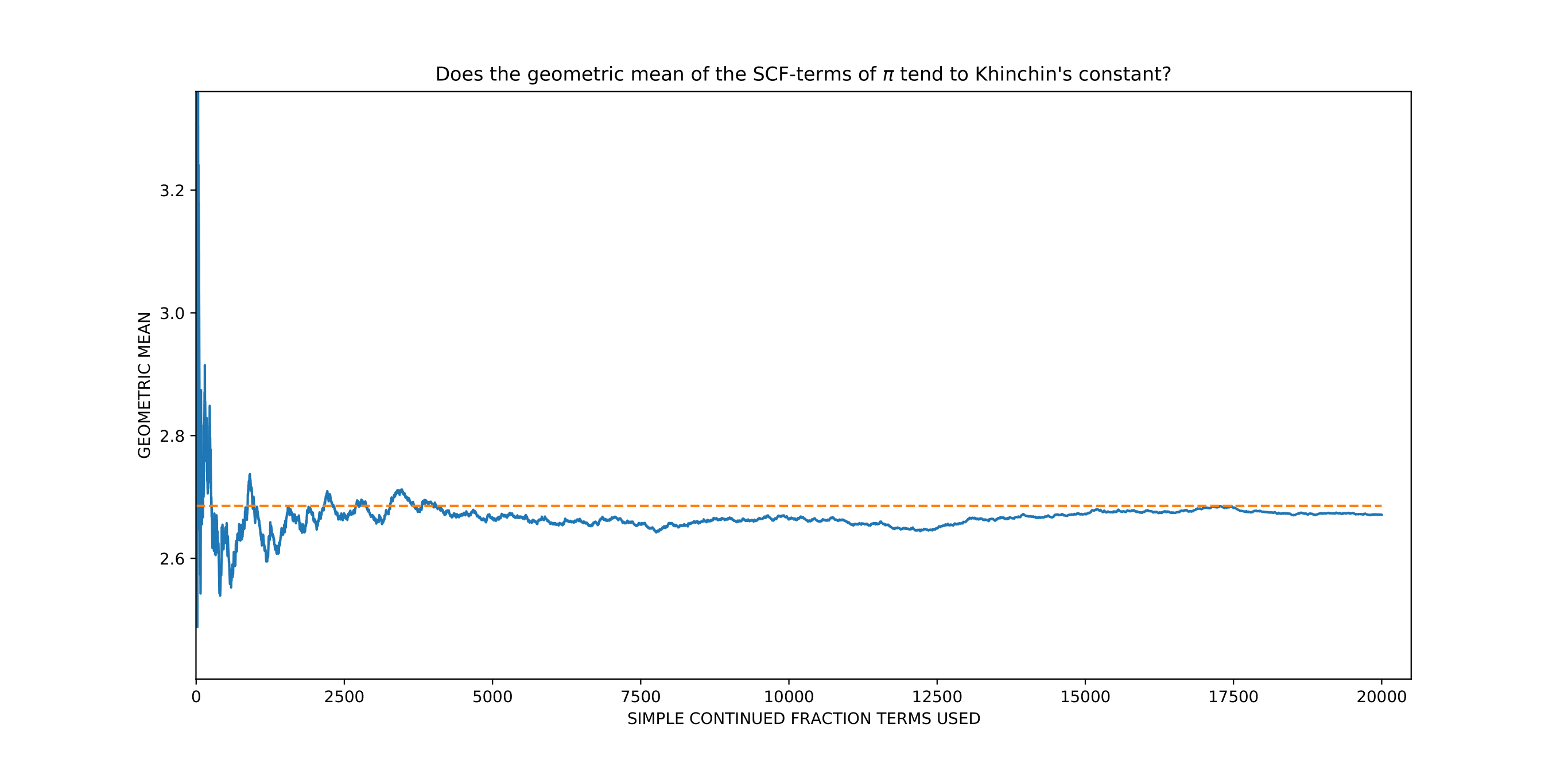
Khinchin's Constant
In number theory, Aleksandr Yakovlevich Khinchin proved that for almost all real numbers ''x'', coefficients ''a''''i'' of the continued fraction expansion of ''x'' have a finite geometric mean that is independent of the value of ''x'' and is known as Khinchin's constant. That is, for :x = a_0+\cfrac\; it is almost always true that :\lim_ \left( a_1 a_2 ... a_n \right) ^ = K_0 where K_0 is Khinchin's constant :K_0 = \prod_^\infty ^ \approx 2.6854520010\dots (with \prod denoting the product over all sequence terms). Although almost all numbers satisfy this property, it has not been proven for ''any'' real number ''not'' specifically constructed for the purpose. Among the numbers whose continued fraction expansions apparently do have this property (based on numerical evidence) are π, the Euler-Mascheroni constant γ, Apéry's constant ζ(3), and Khinchin's constant itself. However, this is unproven. Among the numbers ''x'' whose continued fraction expansions are known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |