|
Kill The Winner Hypothesis
The "Kill the Winner" hypothesis (KTW) is a model of population growth involving prokaryotes, viruses and protozoans that links trophic interactions to biogeochemistry. It is based on the concept of prokaryotes taking one of two reactions to limited resources: "competition", that is, that priority directed to growth of the population, or a "winner"; and "defense", where the resources are directed to survival against attacks. It is then assumed that the better strategy for a phage, or virus which attacks prokaryotes, is to concentrate on the "winner", the most active population (possibly the most abundant). This tends to moderate the relative populations of the prokaryotes, rather than the "winner take all". The model is related to the Lotka–Volterra equations. Current understanding on KTW stems from our knowledge of lytic viruses and their host populations. The competition specialist, or “winner”, often corresponds to the most abundant population in the community. Their abundan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prokaryote
A prokaryote () is a single-celled organism that lacks a nucleus and other membrane-bound organelles. The word ''prokaryote'' comes from the Greek πρό (, 'before') and κάρυον (, 'nut' or 'kernel').Campbell, N. "Biology:Concepts & Connections". Pearson Education. San Francisco: 2003. In the two-empire system arising from the work of Édouard Chatton, prokaryotes were classified within the empire Prokaryota. But in the three-domain system, based upon molecular analysis, prokaryotes are divided into two domains: ''Bacteria'' (formerly Eubacteria) and '' Archaea'' (formerly Archaebacteria). Organisms with nuclei are placed in a third domain, Eukaryota. In the study of the origins of life, prokaryotes are thought to have arisen before eukaryotes. Besides the absence of a nucleus, prokaryotes also lack mitochondria, or most of the other membrane-bound organelles that characterize the eukaryotic cell. It was once thought that prokaryotic cellular components within the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virus
A virus is a wikt:submicroscopic, submicroscopic infectious agent that replicates only inside the living Cell (biology), cells of an organism. Viruses infect all life forms, from animals and plants to microorganisms, including bacteria and archaea. Since Dmitri Ivanovsky's 1892 article describing a non-bacterial pathogen infecting tobacco plants and the discovery of the tobacco mosaic virus by Martinus Beijerinck in 1898,Dimmock p. 4 more than 9,000 virus species have been described in detail of the millions of types of viruses in the environment. Viruses are found in almost every ecosystem on Earth and are the most numerous type of biological entity. The study of viruses is known as virology, a subspeciality of microbiology. When infected, a host cell is often forced to rapidly produce thousands of copies of the original virus. When not inside an infected cell or in the process of infecting a cell, viruses exist in the form of independent particles, or ''virions'', consisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
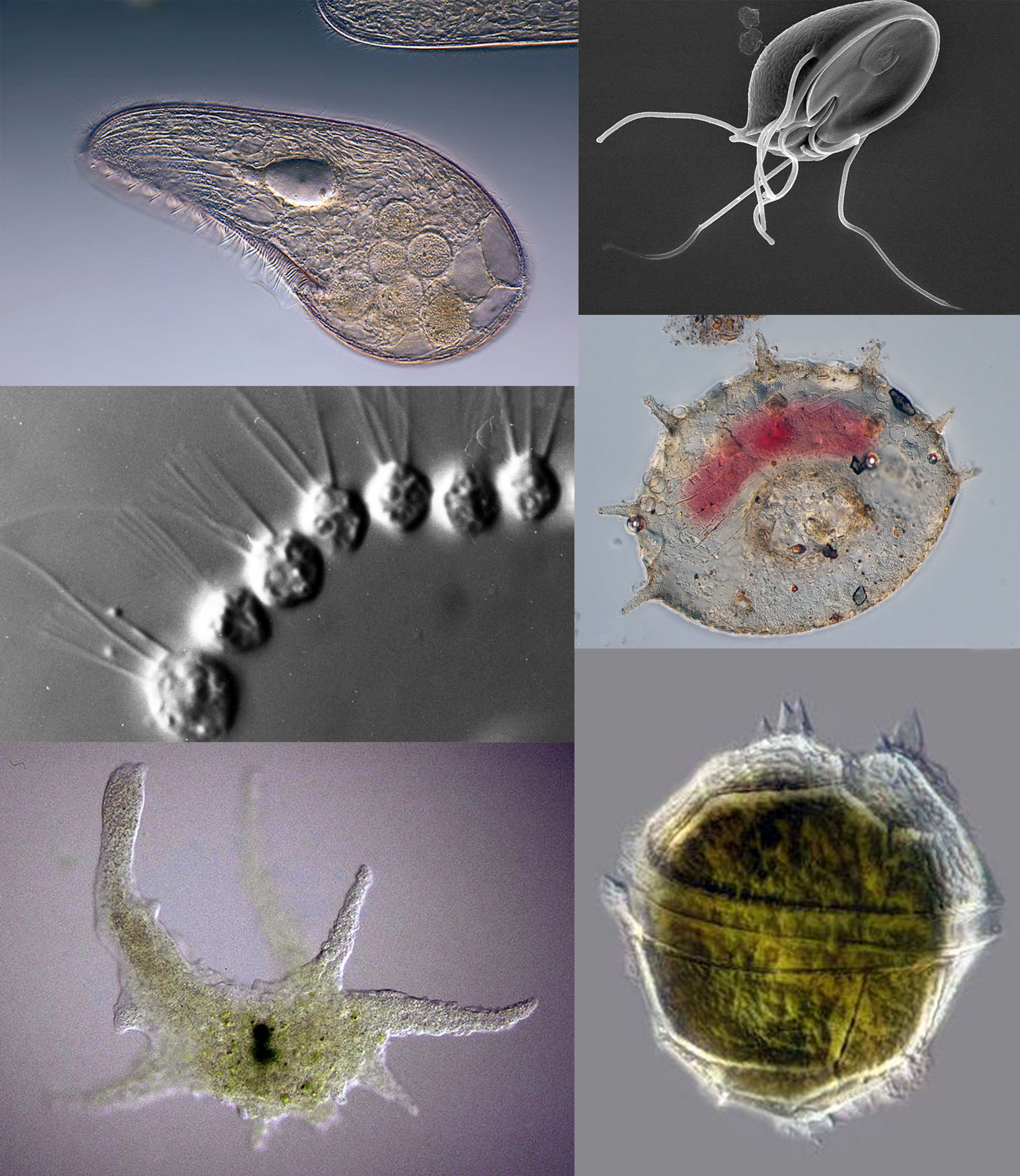
Protozoan
Protozoa (singular: protozoan or protozoon; alternative plural: protozoans) are a group of single-celled eukaryotes, either free-living or parasitic, that feed on organic matter such as other microorganisms or organic tissues and debris. Historically, protozoans were regarded as "one-celled animals", because they often possess animal-like behaviours, such as motility and predation, and lack a cell wall, as found in plants and many algae. When first introduced by Georg Goldfuss (originally spelled Goldfuß) in 1818, the taxon Protozoa was erected as a class within the Animalia, with the word 'protozoa' meaning "first animals". In later classification schemes it was elevated to a variety of higher ranks, including phylum, subkingdom and kingdom, and sometimes included within Protoctista or Protista. The approach of classifying Protozoa within the context of Animalia was widespread in the 19th and early 20th century, but not universal. By the 1970s, it became usual to require ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phage
A bacteriophage (), also known informally as a ''phage'' (), is a duplodnaviria virus that infects and replicates within bacteria and archaea. The term was derived from "bacteria" and the Greek language, Greek φαγεῖν ('), meaning "to devour". Bacteriophages are composed of proteins that Capsid, encapsulate a DNA or RNA genome, and may have structures that are either simple or elaborate. Their genomes may encode as few as four genes (e.g. Bacteriophage MS2, MS2) and as many as hundreds of genes. Phages replicate within the bacterium following the injection of their genome into its cytoplasm. Bacteriophages are among the most common and diverse entities in the biosphere. Bacteriophages are ubiquitous viruses, found wherever bacteria exist. It is estimated there are more than 1031 bacteriophages on the planet, more than every other organism on Earth, including bacteria, combined. Viruses are the most abundant biological entity in the water column of the world's oceans, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lotka–Volterra Equations
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations: \begin \frac &= \alpha x - \beta x y, \\ \frac &= \delta x y - \gamma y, \end where * is the number of prey (for example, rabbits); * is the number of some predator (for example, foxes); *\tfrac and \tfrac represent the instantaneous growth rates of the two populations; * represents time; *, , , are positive real parameters describing the interaction of the two species. The Lotka–Volterra system of equations is an example of a Kolmogorov model, which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism. History The Lotka–Volterra predat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coexistence Theory
Coexistence theory is a framework to understand how competitor traits can maintain species diversity and stave-off competitive exclusion even among similar species living in ecologically similar environments. Coexistence theory explains the stable coexistence of species as an interaction between two opposing forces: fitness differences between species, which should drive the best-adapted species to exclude others within a particular ecological niche, and stabilizing mechanisms, which maintains diversity via niche differentiation. For many species to be stabilized in a community, population growth must be negative density-dependent, i.e. all participating species have a tendency to increase in density as their populations decline. In such communities, any species that becomes rare will experience positive growth, pushing its population to recover and making local extinction unlikely. As the population of one species declines, individuals of that species tend to compete predomin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Community Matrix
In mathematical biology, the community matrix is the linearization of the Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point. The Lotka–Volterra predator–prey model is : \begin \dfrac &=& x(\alpha - \beta y) \\ \dfrac &=& - y(\gamma - \delta x), \end where ''x''(''t'') denotes the number of prey, ''y''(''t'') the number of predators, and ''α'', ''β'', ''γ'' and ''δ'' are constants. By the Hartman–Grobman theorem the non-linear system is topologically equivalent to a linearization of the system about an equilibrium point (''x''*, ''y''*), which has the form : \begin \frac \\ \frac \end = \mathbf \begin u \\ v \end, where ''u'' = ''x'' − ''x''* and ''v'' = ''y'' − ''y''*. In mathematical biology, the Jacobian matrix \mathbf evaluated at the equilibrium point (''x''*, ''y''*) is called the community matrix. By the stable manifold theorem, if one or both eigenvalues of \mathbf ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Dynamics
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems. History Population dynamics has traditionally been the dominant branch of mathematical biology, which has a history of more than 220 years,Malthus, Thomas Robert. An Essay on the Principle of Population: Library of Economics although over the last century the scope of mathematical biology has greatly expanded. The beginning of population dynamics is widely regarded as the work of Malthus, formulated as the Malthusian growth model. According to Malthus, assuming that the conditions (the environment) remain constant ('' ceteris paribus''), a population will grow (or decline) exponentially. This principle provided the basis for the subsequent predictive theories, such as the demographic studies such as the work of Benjamin Gompertz and Pierre François Verhulst in the early 19th century, who refined and adjusted the Malthusian demographic m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Janzen–Connell Hypothesis
The Janzen–Connell hypothesis is a widely accepted explanation for the maintenance of tree species biodiversity in tropical rainforests. It was published independently in the early 1970s by Daniel Janzen and Joseph Connell.Connell, J.H. "On the role of natural enemies in preventing competitive exclusion in some marine animals and in rain forest trees." In: Dynamics of Population. Ed. P.J. Den Boer and G.R. Gradwell. Wageningen: Pudoc, 1970. According to their hypothesis, host-specific herbivores, pathogens, or other natural enemies (often referred to as predators) make the areas near a parent tree (the seed-producing tree) inhospitable for the survival of seedlings. These natural enemies are referred to as 'distance-responsive predators' if they kill seeds or seedlings near the parent tree, or 'density-dependent predators' if they kill seeds or seedlings where they are most abundant (which is typically near the parent tree). Such predators can prevent any one species from dominat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paradox Of Enrichment
The paradox of enrichment is a term from population ecology coined by Michael Rosenzweig in 1971. He described an effect in six predator–prey models where increasing the food available to the prey caused the predator's population to destabilize. A common example is that if the food supply of a prey such as a rabbit is overabundant, its population will grow unbounded and cause the predator population (such as a lynx) to grow unsustainably large. That may result in a crash in the population of the predators and possibly lead to local eradication or even species extinction. The term 'paradox' has been used since then to describe this effect in slightly conflicting ways. The original sense was one of irony; by attempting to increase the carrying capacity in an ecosystem, one could fatally imbalance it. Since then, some authors have used the word to describe the difference between modelled and real predator–prey interactions. Rosenzweig used ordinary differential equation models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |