|
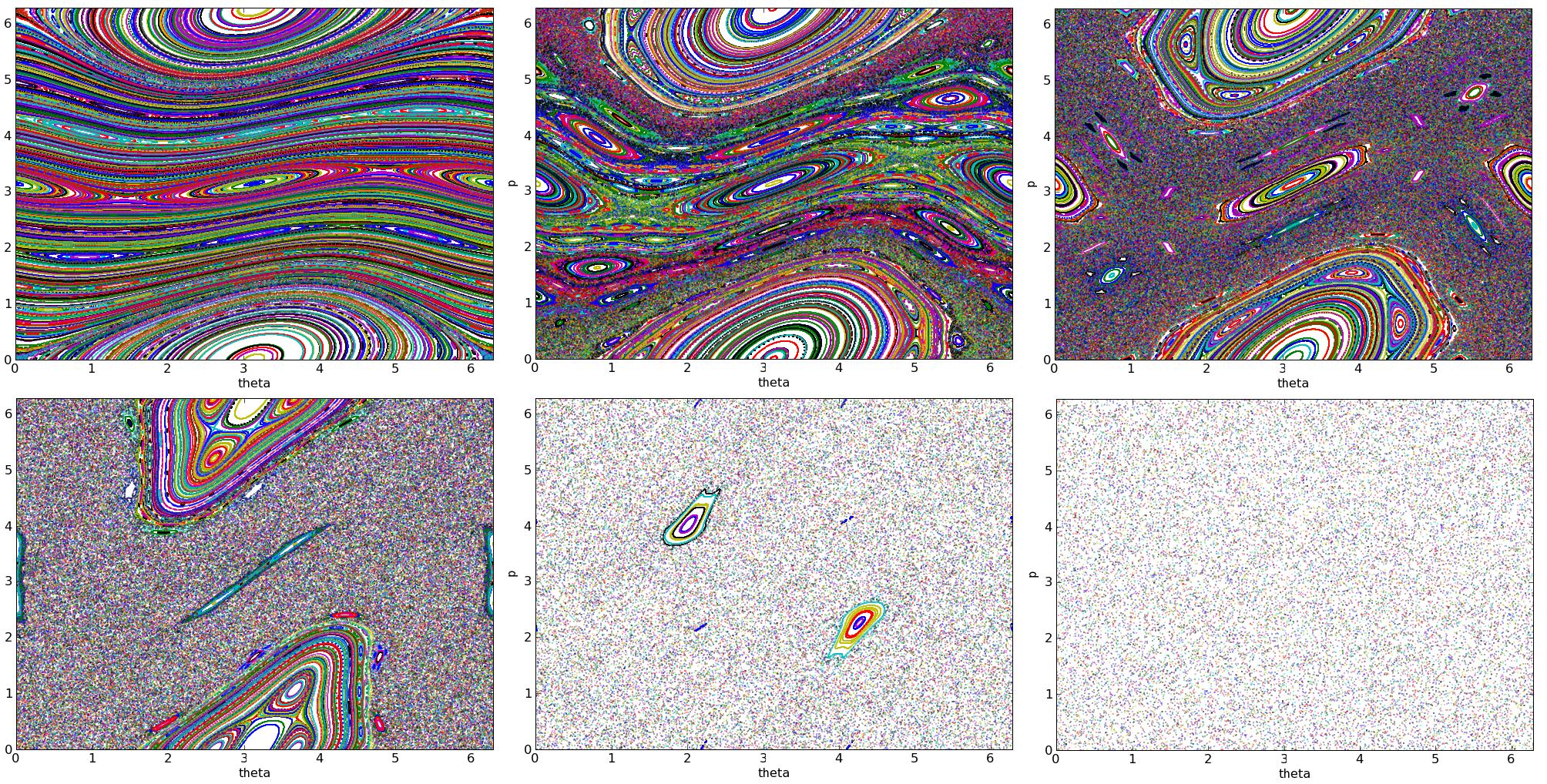
Kicked Rotator
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos (the study of chaos in Hamiltonian systems) and quantum chaos. It describes a free rotating stick (with moment of inertia I) in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian : \mathcal(\theta,p,t)= \frac + K \cos \theta \sum_^\infty \delta \left(\frac-n\right), where \theta \in Dirac delta function. Classical properties Stroboscopic dynamics The equations of motion of the kicked rotator write \frac = \frac = \frac \quad \text \quad \frac = -\frac = K \sin \theta \sum_^\infty \delta \left(\frac-n\right) Theses equations show that between two consecutive kicks, the rotator simply moves freely: the momentum p is conserved and the angular position growths linearly in time. On the other hand, during each kick the momentum abruptly jumps by a quantity K T \sin \theta, where \theta is the an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Map
In mathematics, particularly in dynamical systems, Arnold tongues (named after Vladimir Arnold) Section 12 in page 78 has a figure showing Arnold tongues. are a pictorial phenomenon that occur when visualizing how the rotation number of a dynamical system, or other related invariant property thereof, changes according to two or more of its parameters. The regions of constant rotation number have been observed, for some dynamical systems, to form geometric shapes that resemble tongues, in which case they are called Arnold tongues. Arnold tongues are observed in a large variety of natural phenomena that involve oscillating quantities, such as concentration of enzymes and substrates in biological processes and cardiac electric waves. Sometimes the frequency of oscillation depends on, or is constrained (i.e., ''phase-locked'' or ''mode-locked'', in some contexts) based on some quantity, and it is often of interest to study this relation. For instance, the outset of a tumor triggers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty Principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservative Force
In physics, a conservative force is a force with the property that the total work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the total work done (the sum of the force acting along the path multiplied by the displacement) by a conservative force is zero. A conservative force depends only on the position of the object. If a force is conservative, it is possible to assign a numerical value for the potential at any point and conversely, when an object moves from one location to another, the force changes the potential energy of the object by an amount that does not depend on the path taken, contributing to the mechanical energy and the overall conservation of energy. If the force is not conservative, then defining a scalar potential is not possible, because taking different paths would lead to conflicting potential differences between the start and end points. Gravitational force is an example ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magneto-optical Trap
A magneto-optical trap (MOT) is an apparatus which uses laser cooling and a spatially-varying magnetic field to create a trap which can produce samples of cold, trapped, neutral atoms. Temperatures achieved in a MOT can be as low as several microkelvin, depending on the atomic species, which is two or three times below the photon recoil limit. However, for atoms with an unresolved hyperfine structure, such as ^7\mathrm, the temperature achieved in a MOT will be higher than the Doppler cooling limit. A MOT is formed from the intersection of a weak quadrupolar spatially-varying magnetic field and six circularly-polarized red-detuned optical molasses beams. As atoms travel away from the field zero at the center of the trap (halfway between the coils), the spatially-varying Zeeman shift brings an atomic transition into resonance which gives rise to a scattering force that pushes the atoms back towards the center of the trap. This is why a MOT traps atoms, and because this force aris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mark G
Mark may refer to: Currency * Bosnia and Herzegovina convertible mark, the currency of Bosnia and Herzegovina * East German mark, the currency of the German Democratic Republic * Estonian mark, the currency of Estonia between 1918 and 1927 * Finnish markka ( sv, finsk mark, links=no), the currency of Finland from 1860 until 28 February 2002 * Mark (currency), a currency or unit of account in many nations * Polish mark ( pl, marka polska, links=no), the currency of the Kingdom of Poland and of the Republic of Poland between 1917 and 1924 German * Deutsche Mark, the official currency of West Germany from 1948 until 1990 and later the unified Germany from 1990 until 2002 * German gold mark, the currency used in the German Empire from 1873 to 1914 * German Papiermark, the German currency from 4 August 1914 * German rentenmark, a currency issued on 15 November 1923 to stop the hyperinflation of 1922 and 1923 in Weimar Germany * Lodz Ghetto mark, a special currency for Lodz Ghetto. * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Dissipation
Quantum dissipation is the branch of physics that studies the quantum analogues of the process of irreversible loss of energy observed at the classical level. Its main purpose is to derive the laws of classical dissipation from the framework of quantum mechanics. It shares many features with the subjects of quantum decoherence and quantum theory of measurement. Models The typical approach to describe dissipation is to split the total system in two parts: the quantum system where dissipation occurs, and a so-called environment or bath where the energy of the former will flow towards. The way both systems are coupled depends on the details of the microscopic model, and hence, the description of the bath. To include an irreversible flow of energy (i.e., to avoid Poincaré recurrences in which the energy eventually flows back to the system), requires that the bath contain an infinite number of degrees of freedom. Notice that by virtue of the principle of universality, it is expected t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anderson Localization
In condensed matter physics, Anderson localization (also known as strong localization) is the absence of diffusion of waves in a ''disordered'' medium. This phenomenon is named after the American physicist P. W. Anderson, who was the first to suggest that electron localization is possible in a lattice potential, provided that the degree of randomness (disorder) in the lattice is sufficiently large, as can be realized for example in a semiconductor with impurities or defects. Anderson localization is a general wave phenomenon that applies to the transport of electromagnetic waves, acoustic waves, quantum waves, spin waves, etc. This phenomenon is to be distinguished from weak localization, which is the precursor effect of Anderson localization (see below), and from Mott localization, named after Sir Nevill Mott, where the transition from metallic to insulating behaviour is ''not'' due to disorder, but to a strong mutual Coulomb repulsion of electrons. Introduction In the or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bloch's Theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential take the form of a plane wave modulated by a periodic function. The theorem is named after the physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written where \mathbf is position, \psi is the wave function, u is a periodic function with the same periodicity as the crystal, the wave vector \mathbf is the crystal momentum vector, e is Euler's number, and i is the imaginary unit. Functions of this form are known as Bloch functions or Bloch states, and serve as a suitable basis for the wave functions or states of electrons in crystalline solids. Named after Swiss physicist Felix Bloch, the description of electrons in terms of Bloch functions, termed Bloch electrons (or less often ''Bloch Waves''), underlies the concept of electronic band structures. These eigenstates are written with subscripts as \psi_, where n is a discr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Split-step Method
In numerical analysis, the split-step (Fourier) method is a pseudo-spectral numerical method used to solve nonlinear partial differential equations like the nonlinear Schrödinger equation. The name arises for two reasons. First, the method relies on computing the solution in small steps, and treating the linear and the nonlinear steps separately (see below). Second, it is necessary to Fourier transform back and forth because the linear step is made in the frequency domain while the nonlinear step is made in the time domain. An example of usage of this method is in the field of light pulse propagation in optical fibers, where the interaction of linear and nonlinear mechanisms makes it difficult to find general analytical solutions. However, the split-step method provides a numerical solution to the problem. Another application of the split-step method that has been gaining a lot of traction since the 2010s is the simulation of Kerr frequency comb dynamics in optical microresonato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |