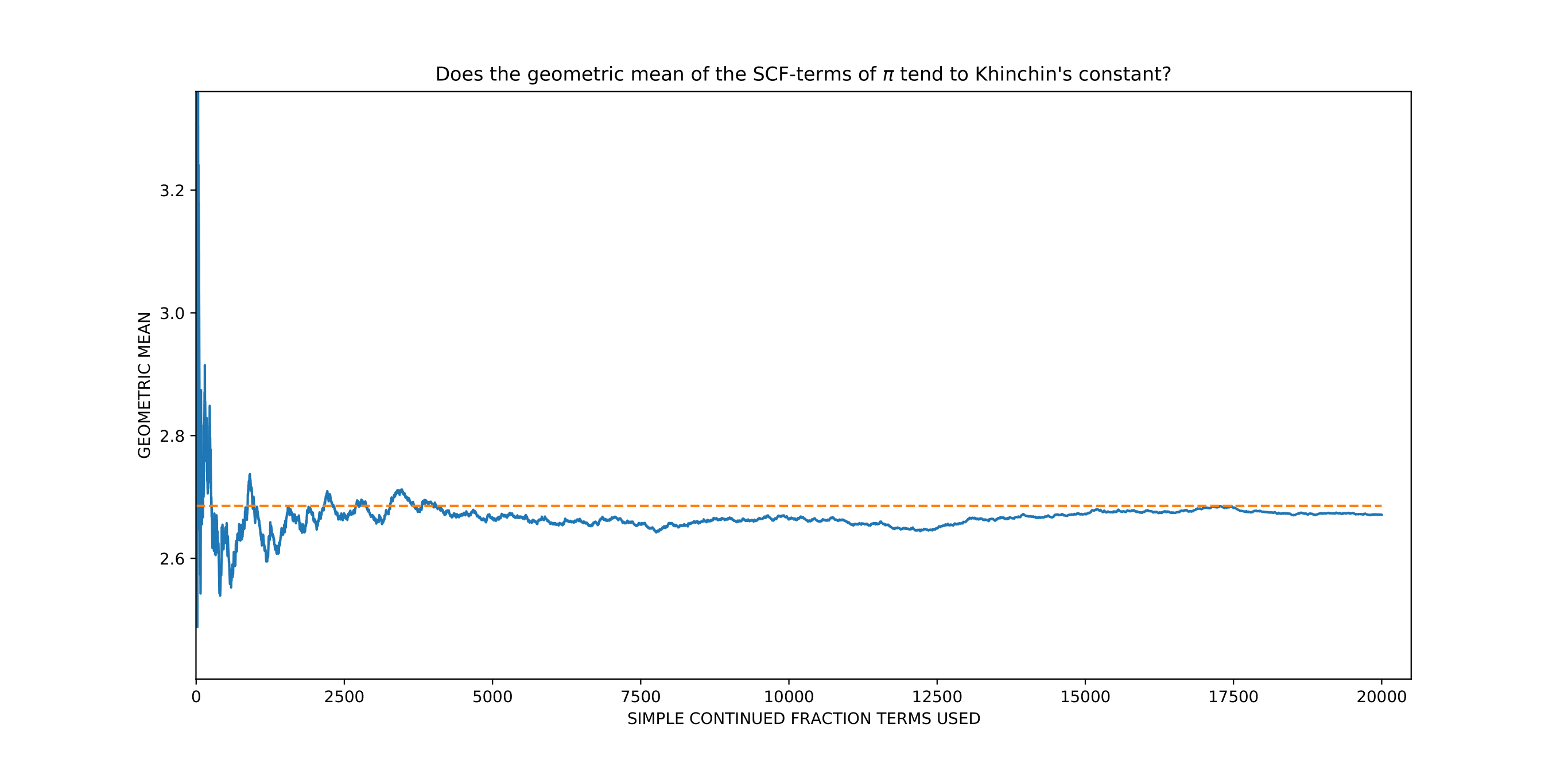
|
Khinchin's Constant
In number theory, Aleksandr Yakovlevich Khinchin proved that for almost all real numbers ''x'', coefficients ''a''''i'' of the continued fraction expansion of ''x'' have a finite geometric mean that is independent of the value of ''x'' and is known as Khinchin's constant. That is, for :x = a_0+\cfrac\; it is almost always true that :\lim_ \left( a_1 a_2 ... a_n \right) ^ = K_0 where K_0 is Khinchin's constant :K_0 = \prod_^\infty ^ \approx 2.6854520010\dots (with \prod denoting the product over all sequence terms). Although almost all numbers satisfy this property, it has not been proven for ''any'' real number ''not'' specifically constructed for the purpose. Among the numbers whose continued fraction expansions apparently do have this property (based on numerical evidence) are π, the Euler-Mascheroni constant γ, Apéry's constant ζ(3), and Khinchin's constant itself. However, this is unproven. Among the numbers ''x'' whose continued fraction expansions are known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1. It is often denoted ' (capital letter ). In addition to its role in real analysis, the unit interval is used to study homotopy theory in the field of topology. In the literature, the term "unit interval" is sometimes applied to the other shapes that an interval from 0 to 1 could take: , , and . However, the notation ' is most commonly reserved for the closed interval . Properties The unit interval is a complete metric space, homeomorphic to the extended real number line. As a topological space, it is compact, contractible, path connected and locally path connected. The Hilbert cube is obtained by taking a topological product of countably many copies of the unit interval. In mathematical analysis, the unit interval is a one-dimensional analytical manifold whose boundary consists of the two points 0 and 1. Its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrable Function
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ergodic Theorem
Ergodic theory (Greek: ' "work", ' "way") is a branch of mathematics that studies statistical properties of deterministic dynamical systems; it is the study of ergodicity. In this context, statistical properties means properties which are expressed through the behavior of time averages of various functions along trajectories of dynamical systems. The notion of deterministic dynamical systems assumes that the equations determining the dynamics do not contain any random perturbations, noise, etc. Thus, the statistics with which we are concerned are properties of the dynamics. Ergodic theory, like probability theory, is based on general notions of measure theory. Its initial development was motivated by problems of statistical physics. A central concern of ergodic theory is the behavior of a dynamical system when it is allowed to run for a long time. The first result in this direction is the Poincaré recurrence theorem, which claims that almost all points in any subset of the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurable Space
In mathematics, a measurable space or Borel space is a basic object in measure theory. It consists of a set and a σ-algebra, which defines the subsets that will be measured. Definition Consider a set X and a σ-algebra \mathcal A on X. Then the tuple (X, \mathcal A) is called a measurable space. Note that in contrast to a measure space, no measure is needed for a measurable space. Example Look at the set: X = \. One possible \sigma-algebra would be: \mathcal A_1 = \. Then \left(X, \mathcal A_1\right) is a measurable space. Another possible \sigma-algebra would be the power set on X: \mathcal A_2 = \mathcal P(X). With this, a second measurable space on the set X is given by \left(X, \mathcal A_2\right). Common measurable spaces If X is finite or countably infinite, the \sigma-algebra is most often the power set on X, so \mathcal A = \mathcal P(X). This leads to the measurable space (X, \mathcal P(X)). If X is a topological space In mathematics, a topological space is, rou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ergodic Transformation
Ergodic theory (Greek: ' "work", ' "way") is a branch of mathematics that studies statistical properties of deterministic dynamical systems; it is the study of ergodicity. In this context, statistical properties means properties which are expressed through the behavior of time averages of various functions along trajectories of dynamical systems. The notion of deterministic dynamical systems assumes that the equations determining the dynamics do not contain any random perturbations, noise, etc. Thus, the statistics with which we are concerned are properties of the dynamics. Ergodic theory, like probability theory, is based on general notions of measure theory. Its initial development was motivated by problems of statistical physics. A central concern of ergodic theory is the behavior of a dynamical system when it is allowed to run for a long time. The first result in this direction is the Poincaré recurrence theorem, which claims that almost all points in any subset of the pha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure-preserving Transformation
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular. Measure-preserving systems obey the Poincaré recurrence theorem, and are a special case of conservative systems. They provide the formal, mathematical basis for a broad range of physical systems, and, in particular, many systems from classical mechanics (in particular, most non-dissipative systems) as well as systems in thermodynamic equilibrium. Definition A measure-preserving dynamical system is defined as a probability space and a measure-preserving transformation on it. In more detail, it is a system :(X, \mathcal, \mu, T) with the following structure: *X is a set, *\mathcal B is a σ-algebra over X, *\mu:\mathcal\rightarrow ,1/math> is a probability measure, so that \mu (X) = 1, and \mu(\varnothing) = 0, * T:X \rightarrow X is a measurable transformation which preserves the measure \mu, i.e., \forall A\in \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence (measure Theory)
In mathematics, and specifically in measure theory, equivalence is a notion of two measures being qualitatively similar. Specifically, the two measures agree on which events have measure zero. Definition Let \mu and \nu be two measures on the measurable space (X, \mathcal A), and let :\mathcal_\mu := \ and :\mathcal_\nu := \ be the sets of \mu-null sets and \nu-null sets, respectively. Then the measure \nu is said to be absolutely continuous in reference to \mu iff \mathcal N_\nu \supseteq \mathcal N_\mu. This is denoted as \nu \ll \mu. The two measures are called equivalent iff \mu \ll \nu and \nu \ll \mu, which is denoted as \mu \sim \nu. That is, two measures are equivalent if they satisfy \mathcal N_\mu = \mathcal N_\nu. Examples On the real line Define the two measures on the real line as : \mu(A)= \int_A \mathbf 1_(x) \mathrm dx : \nu(A)= \int_A x^2 \mathbf 1_(x) \mathrm dx for all Borel sets A . Then \mu and \nu are equivalent, since all sets outside of ,1 have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire probability space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint events by the measure should be the sum of the probabilities of the events; for example, the value assigned to "1 or 2" in a throw of a dice should be the sum of the values assigned to "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a function \mu to be a probability measure on a probability space are that: * \mu must return results in the unit interval , 1 returning 0 for the empty set and 1 for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss–Kuzmin Distribution
In mathematics, the Gauss–Kuzmin distribution is a discrete probability distribution that arises as the limit probability distribution of the coefficients in the continued fraction expansion of a random variable uniform distribution (continuous), uniformly distributed in (0, 1). The distribution is named after Carl Friedrich Gauss, who derived it around 1800, and Rodion Kuzmin, who gave a bound on the rate of convergence in 1929. It is given by the probability mass function : p(k) = - \log_2 \left( 1 - \frac\right)~. Gauss–Kuzmin theorem Let : x = \cfrac be the continued fraction expansion of a random number ''x'' uniformly distributed in (0, 1). Then : \lim_ \mathbb \left\ = - \log_2\left(1 - \frac\right)~. Equivalently, let : x_n = \cfrac~; then : \Delta_n(s) = \mathbb \left\ - \log_2(1+s) tends to zero as ''n'' tends to infinity. Rate of convergence In 1928, Kuzmin gave the bound : , \Delta_n(s), \leq C \exp(-\alpha \sqrt)~. In 1929, Paul Là ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borel Set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets (or, equivalently, from closed sets) through the operations of countable union, countable intersection, and relative complement. Borel sets are named after Émile Borel. For a topological space ''X'', the collection of all Borel sets on ''X'' forms a σ-algebra, known as the Borel algebra or Borel σ-algebra. The Borel algebra on ''X'' is the smallest σ-algebra containing all open sets (or, equivalently, all closed sets). Borel sets are important in measure theory, since any measure defined on the open sets of a space, or on the closed sets of a space, must also be defined on all Borel sets of that space. Any measure defined on the Borel sets is called a Borel measure. Borel sets and the associated Borel hierarchy also play a fundamental role in descriptive set theory. In some contexts, Borel sets are defined to be generated by the compact sets of the topological spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
