|
Kerr–Schild Perturbations
Kerr–Schild perturbations are a special type of perturbation to a spacetime metric which only appear linearly in the Einstein field equations which describe general relativity. They were found by Roy Kerr and Alfred Schild in 1965. Form A generalised Kerr–Schild perturbation has the form h_=V l_a l_b, where V is a scalar and l_a is a null vector with respect to the background spacetime. It can be shown that any perturbation of this form will only appear quadratically in the Einstein equations, and only linearly if the condition l^a \nabla_a l_b =\phi l_b, where \phi is a scalar, is imposed. This condition is equivalent to requiring that the orbits of l^a are geodesics. Applications While the form of the perturbation may appear very restrictive, there are several black hole metrics which can be written in Kerr–Schild form, such as Schwarzschild (stationary black hole), Kerr Kerr may refer to: People * Kerr (surname) * Kerr (given name) Places ;United States * Kerr Townshi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation Theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle step that breaks the problem into "solvable" and "perturbative" parts. In perturbation theory, the solution is expressed as a power series in a small parameter The first term is the known solution to the solvable problem. Successive terms in the series at higher powers of \varepsilon usually become smaller. An approximate 'perturbation solution' is obtained by truncating the series, usually by keeping only the first two terms, the solution to the known problem and the 'first order' perturbation correction. Perturbation theory is used in a wide range of fields, and reaches its most sophisticated and advanced forms in quantum field theory. Perturbation theory (quantum mechanics) describes the use of this method in quantum mechanics. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime Metric
In general relativity, the metric tensor (in this context often abbreviated to simply the metric) is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational potential of Newtonian gravitation. The metric captures all the geometric and causal structure of spacetime, being used to define notions such as time, distance, volume, curvature, angle, and separation of the future and the past. Notation and conventions Throughout this article we work with a metric signature that is mostly positive (); see sign convention. The gravitation constant G will be kept explicit. This article employs the Einstein summation convention, where repeated indices are automatically summed over. Definition Mathematically, spacetime is represented by a four-dimensional differentiable manifold M and the metric tensor is given as a covariant, second-degree, symmetric tensor on M, conventionally denoted by g. Moreover, the metric is required to be nondegenera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roy Kerr
Roy Patrick Kerr (; born 16 May 1934) is a New Zealand mathematician who discovered the Kerr geometry, an exact solution to the Einstein field equation of general relativity. His solution models the gravitational field outside an uncharged rotating massive object, including a rotating black hole.''Cracking the Einstein Code'' by , 2009 His solution to Einstein's equations predicted spinning black holes before they were discovered. Early life and education Kerr was born in 1934 in Kurow, New Zealand. He was born into a dys ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred Schild
Alfred Schild (September 7, 1921 – May 24, 1977) was a leading Austrian American physicist, well known for his contributions to the Golden age of general relativity (1960–1975). Biography Schild was born in Istanbul on September 7, 1921. His parents were German-speaking Viennese Jews, but his early education was in England. Upon the outbreak of World War II Schild was interned as an enemy alien, but later allowed to travel to Canada. In 1944 he earned his B.A. at the University of Toronto, and in 1946 completed his doctorate under the direction of Leopold Infeld. Schild spent the next eleven years at the Carnegie Institute of Technology, where he helped to develop the first atomic clocks. As tensors are the language of general relativity, Schild wrote ''Tensor Calculus'' with John L. Synge as a textbook. According to a reviewer, "The ideas and concepts are given very concisely and thus a wide range of subjects is considered." In 1957 he moved to the University of Texas at Au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his more complete and modern-looking discussion four months after Schwarzschild. According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Sch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
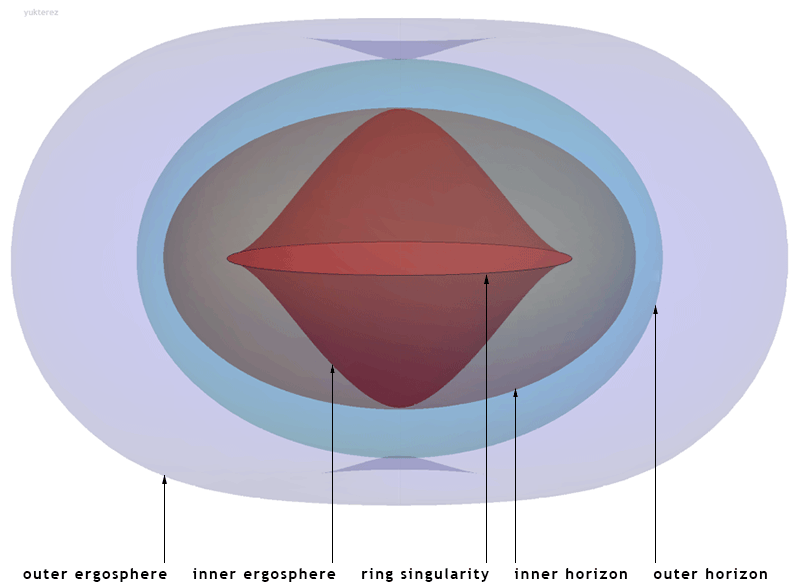
Kerr Metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reissner–Nordström Metric
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass ''M''. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric. The metric was discovered between 1916 and 1921 by Hans Reissner, Hermann Weyl, Gunnar Nordström and George Barker Jeffery independently. The metric In spherical coordinates (t, r, \theta, \varphi), the Reissner–Nordström metric (i.e. the line element) is ds^2=c^2\, d\tau^2 = \left( 1 - \frac + \frac \right) c^2\, dt^2 -\left( 1 - \frac + \frac \right)^ \, dr^2 - r^2 \, d\theta^2 - r^2\sin^2\theta \, d\varphi^2, where c is the speed of light, \tau is the proper time, t is the time coordinate (measured by a stationary clock at infinity), r is the radial coordinate, (\theta, \varphi) are the spherical angles, and r_\text is the Schwarzschil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr–Newman Metric
The Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions, that is, of solutions to the Einstein–Maxwell equations which account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions. This solution has not been especially useful for describing astrophysical phenomena, because observed astronomical objects do not possess an appreciable net electric charge, and the magnetic fields of stars arise through other processes. As a model of realistic black ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |