|
Kerr–Newman–de–Sitter Metric
The Kerr–Newman–de–Sitter metric (KNdS) is one of the most general stationary spacetime, stationary solutions of the Einstein's field equation#Einstein–Maxwell equations, Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass embedded in an expanding universe. It generalizes the Kerr–Newman metric by taking into account the cosmological constant \Lambda. Boyer–Lindquist coordinates In those coordinates the local clocks and rulers are at constant \rm r and have no local orbital angular momentum \rm (L_z=0), therefore they are corotating with the frame-dragging velocity relative to the fixed stars. In Metric signature, signature and in Nondimensionalization, natural units of \rm G=M=c=k_e=1 the KNdS metric is g_= \rm -\frac g_= \rm -\frac g_= \rm -\frac g_= \rm\frac g_= \rm \frac with all the other metric tensor components g_=0, where \rm a is the black hole's spi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Spacetime
In general relativity, specifically in the Einstein field equations, a spacetime is said to be stationary if it admits a Killing vector that is Asymptotic curve, asymptotically timelike. Description and analysis In a stationary spacetime, the metric tensor components, g_, may be chosen so that they are all independent of the time coordinate. The line element of a stationary spacetime has the form (i,j = 1,2,3) : ds^ = \lambda (dt - \omega_\, dy^i)^ - \lambda^ h_\, dy^i\,dy^j, where t is the time coordinate, y^ are the three spatial coordinates and h_ is the metric tensor of 3-dimensional space. In this coordinate system the Killing vector field \xi^ has the components \xi^ = (1,0,0,0). \lambda is a positive scalar representing the norm of the Killing vector, i.e., \lambda = g_\xi^\xi^, and \omega_ is a 3-vector, called the twist vector, which vanishes when the Killing vector is hypersurface orthogonal. The latter arises as the spatial components of the twist 4-vector \omega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Parameter
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line". The noun ''geodesic'' and the adjective ''geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Sitter Space
In mathematical physics, ''n''-dimensional de Sitter space (often denoted dS''n'') is a maximally symmetric Lorentzian manifold with constant positive scalar curvature. It is the Lorentzian analogue of an ''n''-sphere (with its canonical Riemannian metric). The main application of de Sitter space is its use in general relativity, where it serves as one of the simplest mathematical models of the universe consistent with the observed accelerating expansion of the universe. More specifically, de Sitter space is the maximally symmetric vacuum solution of Einstein's field equations in which the cosmological constant \Lambda is positive (corresponding to a positive vacuum energy density and negative pressure). De Sitter space and anti-de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked closely together in Le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kretschmann Scalar
In the theory of pseudo-Riemannian manifold, Lorentzian manifolds, particularly in the context of applications to general relativity, the Kretschmann scalar is a quadratic curvature invariant (general relativity), scalar invariant. It was introduced by Erich Kretschmann. Definition The Kretschmann invariant is : K = R_ \, R^ where R^_ = \partial_\Gamma^_ - \partial_\Gamma^_ + \Gamma^_\Gamma^_ - \Gamma^_\Gamma^_ is the Riemann curvature tensor and \Gamma is the Christoffel symbol. Because it is a sum of squares of tensor components, this is a ''quadratic'' invariant. Einstein summation convention with Raising_and_lowering_indices, raised and lowered indices is used above and throughout the article. An explicit summation expression is : K = R_ \, R^ =\sum_^\sum_^3 \sum_^3\sum_^3 R_ \, R^ \text R^ =\sum_^3 g^\,\sum_^3 g^\,\sum_^3 g^\,\sum_^3 g^\, R_. \, Examples For a Schwarzschild metric, Schwarzschild black hole of mass M, the Kretschmann scalar is : K = \frac \,. whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ricci Curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space. The Ricci tensor can be characterized by measurement of how a shape is deformed as one moves along geodesics in the space. In general relativity, which involves the pseudo-Riemannian setting, this is reflected by the presence of the Ricci tensor in the Raychaudhuri equation. Partly for this reason, the Einstein field equations propose that spacetime can be described by a pseudo-Riemannian metric, with a strikingly simple relationship between the Ricci tensor and the matter content of the universe. Like the metric tensor, the Ricci tensor assigns to each tangent space of the manifold a symmetric bi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Sitter–Schwarzschild Metric
In general relativity, the de Sitter–Schwarzschild solution describes a black hole in a causal patch of de Sitter space. It is the positive-curvature case of the Kottler metric. Unlike a flat-space black hole, there is a largest possible de Sitter black hole, which is the Nariai spacetime (named after ). The Nariai limit has no singularities, the cosmological and black hole horizons have the same area, and they can be mapped to each other by a discrete reflection symmetry in any causal patch. Introduction In general relativity, spacetimes can have black hole event horizons and also cosmological horizons. The de Sitter–Schwarzschild solution is the simplest solution that has both. Metric The metric of any spherically symmetric solution in Schwarzschild form is: : ds^2 = - f(r) dt^2 + + r^2(d\theta^2 + \sin^2\theta \,d\phi^2) The vacuum Einstein equations give a ''linear'' equation for ''f''(''r''), which has as solutions: : f(r)=1-2a/r : f(r)= 1 - b r^2 The fir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anti-de Sitter Space
In mathematics and physics, ''n''-dimensional anti-de Sitter space (AdS''n'') is a symmetric_space, maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (6 May 1872 – 20 November 1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963. Manifolds of constant curvature are most familiar in the case of two dimensions, where the elliptic plane or surface of a sphere is a surface of constant positive curvature, a flat (i.e., Euclidean space, Euclidean) plane is a surface of constant zero curvature, and a hyperbolic plane is a surface of constant negative curvature. Einstein's general theory of relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ring Singularity
A ring singularity or ringularity is the gravitational singularity of a rotating black hole, or a Kerr black hole, that is shaped like a ring. Description When a spherical non-rotating body of a critical radius collapses under its own gravitation under general relativity, theory suggests it will collapse to a 0-dimensional single point. This is not the case with a rotating black hole (a Kerr black hole). With a fluid rotating body, its distribution of mass is not spherical (it shows an equatorial bulge), and it has angular momentum. Since a point cannot support rotation or angular momentum in classical physics (general relativity being a classical theory), the minimal shape of the singularity that can support these properties is instead a 2D ring with zero thickness but non-zero radius, and this is referred to as a ringularity or Kerr singularity. A rotating hole's rotational frame-dragging effects, described by the Kerr metric, cause spacetime in the vicinity of the ring to unde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiverse
The multiverse is the hypothetical set of all universes. Together, these universes are presumed to comprise everything that exists: the entirety of space, time, matter, energy, information, and the physical laws and constants that describe them. The different universes within the multiverse are called "parallel universes", "flat universes", "other universes", "alternate universes", "multiple universes", "plane universes", "parent and child universes", "many universes", or "many worlds". One common assumption is that the multiverse is a "patchwork quilt of separate universes all bound by the same laws of physics." The concept of multiple universes, or a multiverse, has been discussed throughout history. It has evolved and has been debated in various fields, including cosmology, physics, and philosophy. Some physicists have argued that the multiverse is a philosophical notion rather than a scientific hypothesis, as it cannot be empirically falsified. In recent years, there h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr Metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
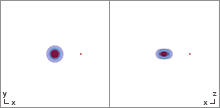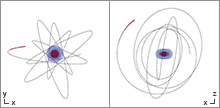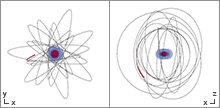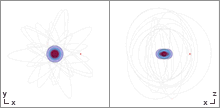
Orbit In The Kerr Newman De Sitter Spacetime
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr Newman De Sitter (KNdS) Horizons Vs Ergospheres
Kerr may refer to: People *Kerr (surname) *Kerr (given name) Places ;United States *Kerr Township, Champaign County, Illinois *Kerr, Montana, A US census-designated place *Kerr, Ohio, an unincorporated community *Kerr County, Texas Other uses *KERR, A US radio station *Kerr, a brand of food Mason jars and lids *Clan Kerr Clan Kerr () is a Scottish clan whose origins lie in the Scottish Borders. During the Middle Ages, it was one of the prominent border reiver clans along the present-day Anglo-Scottish border and played an important role in the history of th ..., a Scottish clan See also * * * Ker (other) {{Disambiguation, geo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |