|
Kendall's Notation
In queueing theory, a discipline within the mathematical theory of probability, Kendall's notation (or sometimes Kendall notation) is the standard system used to describe and classify a queueing node. D. G. Kendall proposed describing queueing models using three factors written A/S/''c'' in 1953 where A denotes the time between arrivals to the queue, S the service time distribution and ''c'' the number of service channels open at the node. It has since been extended to A/S/''c''/''K''/''N''/D where ''K'' is the capacity of the queue, ''N'' is the size of the population of jobs to be served, and D is the queueing discipline. When the final three parameters are not specified (e.g. M/M/1 queue), it is assumed ''K'' = ∞, ''N'' = ∞ and D = FIFO. A: The arrival process A code describing the arrival process. The codes used are: S: The service time distribution This gives the distribution of time of the service of a customer. Some common notations are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D/M/1 Queue
In queueing theory, a discipline within the mathematical theory of probability, a D/M/1 queue represents the queue length in a system having a single server, where arrivals occur at fixed regular intervals and job service requirements are random with an exponential distribution. The model name is written in Kendall's notation. Agner Krarup Erlang first published a solution to the stationary distribution of a D/M/1 and D/M/''k'' queue, the model with ''k'' servers, in 1917 and 1920. Model definition A D/M/1 queue is a stochastic process whose state space is the set where the value corresponds to the number of customers in the system, including any currently in service. * Arrivals occur deterministically at fixed times ''β'' apart. * Service times are exponentially distributed (with rate parameter ''μ''). * A single server serves customers one at a time from the front of the queue, according to a first-come, first-served Queueing theory is the mathematical study of waiting li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arrival Rate
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang when he created models to describe the system of Copenhagen Telephone Exchange company, a Danish company. The ideas have since seen applications including telecommunication, traffic engineering, computing and, particularly in industrial engineering, in the design of factories, shops, offices and hospitals, as well as in project management. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is ''Queueing Systems''. Single queueing nodes A queue, or queueing node ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Arrival Rate
Effectiveness is the capability of producing a desired result or the ability to produce desired output. When something is deemed effective, it means it has an intended or expected outcome, or produces a deep, vivid impression. Etymology The origin of the word "effective" stems from the Latin word effectīvus, which means creative, productive or effective. It surfaced in Middle English between 1300 and 1400 A.D. Usage In mathematics and logic, ''effective'' is used to describe metalogical methods that fit the criteria of an effective procedure. In group theory, a group element acts ''effectively'' (or ''faithfully'') on a point, if that point is not fixed by the action. In physics, an effective theory is, similar to a phenomenological theory, a framework intended to explain certain (observed) effects without the claim that the theory correctly models the underlying (unobserved) processes. In heat transfer, ''effectiveness'' is a measure of the performance of a heat excha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
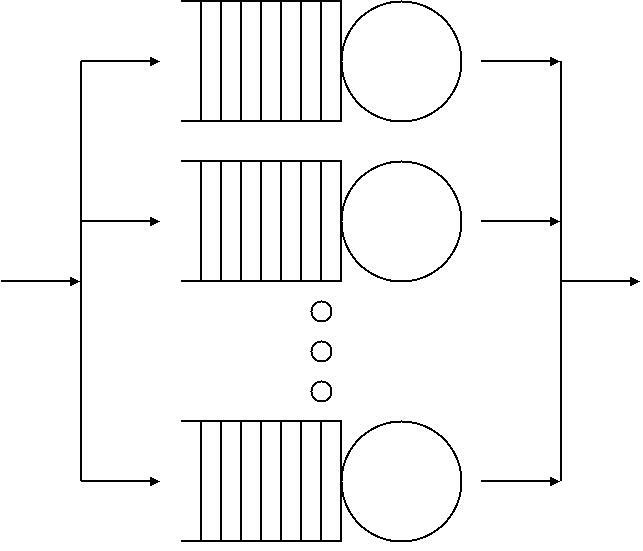
M/M/c Queue
In queueing theory, a discipline within , the queue (or Erlang–T model) is a multi-server queueing model. In Kendall's notation it describes a system where arrivals form a single queue and are governed by a , there are servers, and job service times are exponentially distributed. It is a generalization of which considers only a single server. The model with infinitely many servers is the M/M/∞ queue. Model definition An M/M/c queue is a stochastic process whose state space is the set where the value corresponds to the number of customers in the system, including any currently in service. * Arrivals occur at rate according to a Poisson process and move the process from state to +1. * Service times have an exponential distribution with parameter . If there are fewer than jobs, some of the servers will be idle. If there are more than jobs, the jobs queue in a buffer. * The buffer is of infinite size, so there is no limit on the number of customers it can contain. The mode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/G/1 Queue
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian (modulated by a Poisson process), service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk. Model definition A queue represented by a M/G/1 queue is a stochastic process whose state space is the set , where the value corresponds to the number of customers in the queue, including any being served. Transitions from state ''i'' to ''i'' + 1 represent the arrival of a new customer: the times between such arrivals have an exponential distribution with parameter λ. Transitions from state ''i'' to ''i'' − 1 represent a customer who has been served, finishing being served and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/D/1 Queue
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue. Model definition An M/D/1 queue is a stochastic process whose state space is the set where the value corresponds to the number of entities in the system, including any currently in service. * Arrivals occur at rate λ according to a Poisson process and move the process from state ''i'' to ''i'' + 1. * Service times are deterministic time ''D'' (serving at rate ''μ'' = 1/''D''). * A single server serves entities one at a time from the front of the queue, according to a first-come, first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase-type Distribution
A phase-type distribution is a probability distribution constructed by a convolution or mixture of exponential distributions. It results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occurs may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of a Markov process with one absorbing state. Each of the states of the Markov process represents one of the phases. It has a discrete-time equivalent the discrete phase-type distribution. The set of phase-type distributions is dense in the field of all positive-valued distributions, that is, it can be used to approximate any positive-valued distribution. Definition Consider a continuous-time Markov process with ''m'' + 1 states, where ''m'' ≥ 1, such that the states 1,...,''m'' are transient states and state 0 is an absorbing state. Further, let the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent And Identically Distributed Random Variables
In probability theory and statistics, a collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent. This property is usually abbreviated as ''i.i.d.'', ''iid'', or ''IID''. IID was first defined in statistics and finds application in different fields such as data mining and signal processing. Introduction In statistics, we commonly deal with random samples. A random sample can be thought of as a set of objects that are chosen randomly. Or, more formally, it’s “a sequence of independent, identically distributed (IID) random variables”. In other words, the terms ''random sample'' and ''IID'' are basically one and the same. In statistics, we usually say “random sample,” but in probability it’s more common to say “IID.” * Identically Distributed means that there are no overall trends–the distribution doesn’t fluctuate and all items in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Parameter
In probability theory and statistics, a shape parameter (also known as form parameter) is a kind of numerical parameter of a parametric family of probability distributionsEveritt B.S. (2002) Cambridge Dictionary of Statistics. 2nd Edition. CUP. that is neither a location parameter nor a scale parameter (nor a function of these, such as a rate parameter). Such a parameter must affect the ''shape'' of a distribution rather than simply shifting it (as a location parameter does) or stretching/shrinking it (as a scale parameter does). For example, "peakedness" refers to how round the main peak is. Estimation Many estimators measure location or scale; however, estimators for shape parameters also exist. Most simply, they can be estimated in terms of the higher moments, using the method of moments, as in the ''skewness'' (3rd moment) or ''kurtosis'' (4th moment), if the higher moments are defined and finite. Estimators of shape often involve higher-order statistics (non-linear fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erlang Distribution
The Erlang distribution is a two-parameter family of continuous probability distributions with support x \in exponential distribution">exponential variables with mean 1/\lambda each. Equivalently, it is the distribution of the time until the ''k''th event of a Poisson process with a rate of \lambda. The Erlang and Poisson distributions are complementary, in that while the Poisson distribution counts the number of events that occur in a fixed amount of time, the Erlang distribution counts the amount of time until the occurrence of a fixed number of events. When k=1, the distribution simplifies to the exponential distribution. The Erlang distribution is a special case of the gamma distribution wherein the shape of the distribution is discretised. The Erlang distribution was developed by Agner Krarup Erlang, A. K. Erlang to examine the number of telephone calls which might be made at the same time to the operators of the switching stations. This work on telephone Teletraffic en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |