|
Josephson Constant
The magnetic flux, represented by the symbol , threading some contour or loop is defined as the magnetic field multiplied by the loop area , i.e. . Both and can be arbitrary, meaning can be as well. However, if one deals with the superconducting loop or a hole in a bulk superconductor, the magnetic flux threading such a hole/loop is actually quantized. The (superconducting) magnetic flux quantum ≈ is a combination of fundamental physical constants: the Planck constant and the electron charge . Its value is, therefore, the same for any superconductor. The phenomenon of flux quantization was discovered experimentally by B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Näbauer, in 1961. The quantization of magnetic flux is closely related to the Little–Parks effect, but was predicted earlier by Fritz London in 1948 using a phenomenological model. The inverse of the flux quantum, , is called the Josephson constant, and is denoted J. It is the consta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weber (unit)
In physics, the weber ( ; symbol: Wb) is the unit of magnetic flux in the International System of Units (SI), whose units are volt-second. A magnetic flux density of one Wb/m2 (one weber per square metre) is one tesla. The weber is named after the German physicist Wilhelm Eduard Weber (1804–1891). Definition The weber may be defined in terms of Faraday's law, which relates a changing magnetic flux through a loop to the electric field around the loop. A change in flux of one weber per second will induce an electromotive force of one volt (produce an electric potential difference of one volt across two open-circuited terminals). Officially: That is: \mathrm = \mathrm\mathrm. One weber is also the total magnetix flux across a surface of one square meter perpendicular to a magnetic flux density of one tesla; that is, \mathrm = \mathrm\mathrm^2. Expressed only in SI base units, 1 tesla is: \mathrm = \dfrac. The weber is used in the definition of the henry as 1 weber per am ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Current
In quantum mechanics, the probability current (sometimes called probability flux) is a mathematical quantity describing the flow of probability. Specifically, if one thinks of probability as a heterogeneous fluid, then the probability current is the rate of flow of this fluid. It is a real vector that changes with space and time. Probability currents are analogous to mass currents in hydrodynamics and electric currents in electromagnetism. As in those fields, the probability current is related to the probability density function via a continuity equation. The probability current is invariant under gauge transformation. The concept of probability current is also used outside of quantum mechanics, when dealing with probability density functions that change over time, for instance in Brownian motion and the Fokker–Planck equation. Definition (non-relativistic 3-current) Free spin-0 particle In non-relativistic quantum mechanics, the probability current j of the wave function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Klitzing Constant
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhibits steps that take on the quantized values : R_ = \frac = \frac , where is the Hall voltage, is the channel current, is the elementary charge and is Planck's constant. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively. The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation correspond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2019 Redefinition Of The SI Base Units
In 2019, four of the seven SI base units specified in the International System of Quantities were redefined in terms of natural physical constants, rather than human artifacts such as the standard kilogram. Effective 20 May 2019, the 144th anniversary of the Metre Convention, the kilogram, ampere, kelvin, and mole are now defined by setting exact numerical values, when expressed in SI units, for the Planck constant ('), the elementary electric charge ('), the Boltzmann constant (), and the Avogadro constant (), respectively. The second, metre, and candela had previously been redefined using physical constants. The four new definitions aimed to improve the SI without changing the value of any units, ensuring continuity with existing measurements. In November 2018, the 26th General Conference on Weights and Measures (CGPM) unanimously approved these changes, The conference ran from 13–16 November and the vote on the redefinition was scheduled for the last day. Kazak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superconducting Coherence Length
In superconductivity, the superconducting coherence length, usually denoted as \xi (Greek lowercase ''xi''), is the characteristic exponent of the variations of the density of superconducting component. The superconducting coherence length is one of two parameters in the Ginzburg–Landau theory of superconductivity. It is given by: : \xi = \sqrt where \alpha is a constant in the Ginzburg–Landau theory#Simple interpretation, Ginzburg–Landau equation for \psi with the form \alpha_0 (T-T_c). In Landau mean-field theory, at temperatures ''T'' near the superconducting critical temperature ''Tc'' , ''ξ(T) ∝ (1-T/Tc)−1/2''. Up to a factor of \sqrt, it is equivalent characteristic exponent describing a recovery of the order parameter away from a perturbation in the theory of the second order phase transitions. In some special limiting case (mathematics), limiting cases, for example in the weak-coupling BCS theory of isotropic s-wave superconductor it is related to characteri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abrikosov Vortex
In superconductivity, fluxon (also called a Abrikosov vortex and quantum vortex) is a vortex of supercurrent in a type-II superconductor, used by Alexei Abrikosov to explain magnetic behavior of type-II superconductors. Abrikosov vortices occur generically in the Ginzburg–Landau theory of superconductivity. Overview The solution is a combination of fluxon solution by Fritz London, combined with a concept of core of quantum vortex by Lars Onsager. In the quantum vortex, supercurrent circulates around the normal (i.e. non-superconducting) core of the vortex. The core has a size \sim\xi — the superconducting coherence length (parameter of a Ginzburg–Landau theory). The supercurrents decay on the distance about \lambda (London penetration depth) from the core. Note that in type-II superconductors \lambda>\xi/\sqrt. The circulating supercurrents induce magnetic fields with the total flux equal to a single flux quantum \Phi_0. Therefore, an Abrikosov vortex is often called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type II Superconductor
In superconductivity, a type-II superconductor is a superconductor that exhibits an intermediate phase of mixed ordinary and superconducting properties at intermediate temperature and fields above the superconducting phases. It also features the formation of magnetic field vortices with an applied external magnetic field. This occurs above a certain critical field strength ''Hc1''. The vortex density increases with increasing field strength. At a higher critical field ''Hc2'', superconductivity is destroyed. Type-II superconductors do not exhibit a complete Meissner effect. History In 1935, Rjabinin and Shubnikov experimentally discovered the Type-II superconductors. In 1950, the theory of the two types of superconductors was further developed by Lev Landau and Vitaly Ginzburg in their paper on Ginzburg–Landau theory. In their argument, a type-I superconductor had positive free energy of the superconductor-normal metal boundary. Ginzburg and Landau pointed out the possibilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetometer
A magnetometer is a device that measures magnetic field or magnetic dipole moment. Different types of magnetometers measure the direction, strength, or relative change of a magnetic field at a particular location. A compass is one such device, one that measures the direction of an ambient magnetic field, in this case, the Earth's magnetic field. Other magnetometers measure the magnetic dipole moment of a magnetic material such as a ferromagnet, for example by recording the effect of this magnetic dipole on the induced current in a coil. The first magnetometer capable of measuring the absolute magnetic intensity at a point in space was invented by Carl Friedrich Gauss in 1833 and notable developments in the 19th century included the Hall effect, which is still widely used. Magnetometers are widely used for measuring the Earth's magnetic field, in geophysical surveys, to detect magnetic anomalies of various types, and to determine the dipole moment of magnetic materials. In an air ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SQUID
True squid are molluscs with an elongated soft body, large eyes, eight arms, and two tentacles in the superorder Decapodiformes, though many other molluscs within the broader Neocoleoidea are also called squid despite not strictly fitting these criteria. Like all other cephalopods, squid have a distinct head, bilateral symmetry, and a mantle. They are mainly soft-bodied, like octopuses, but have a small internal skeleton in the form of a rod-like gladius (cephalopod), gladius or pen, made of chitin. Squid diverged from other cephalopods during the Jurassic and occupy a similar role to teleost fish as open water predators of similar size and behaviour. They play an important role in the open water food web. The two long tentacles are used to grab prey and the eight arms to hold and control it. The beak then cuts the food into suitable size chunks for swallowing. Squid are rapid swimmers, moving by Aquatic locomotion#Jet propulsion, jet propulsion, and largely locate their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
London Penetration Depth
In superconductors, the London penetration depth (usually denoted as \lambda or \lambda_L) characterizes the distance to which a magnetic field penetrates into a superconductor and becomes equal to e^ times that of the magnetic field at the surface of the superconductor. Typical values of λL range from 50 to 500 nm. The London penetration depth results from considering the London equation and Ampère's circuital law. If one considers a superconducting half-space, i.e superconducting for x>0, and weak external magnetic field B0 applied along ''z'' direction in the empty space ''x''<0, then inside the superconductor the magnetic field is given by can be seen as the distance across in which the magnetic field becomes times weaker. The form of is found by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meissner Effect
The Meissner effect (or Meissner–Ochsenfeld effect) is the expulsion of a magnetic field from a superconductor during its transition to the superconducting state when it is cooled below the critical temperature. This expulsion will repel a nearby magnet. The German physicists Walther Meissner and Robert Ochsenfeld discovered this phenomenon in 1933 by measuring the magnetic field distribution outside superconducting tin and lead samples. The samples, in the presence of an applied magnetic field, were cooled below their superconducting transition temperature, whereupon the samples cancelled nearly all interior magnetic fields. They detected this effect only indirectly because the magnetic flux is conserved by a superconductor: when the interior field decreases, the exterior field increases. The experiment demonstrated for the first time that superconductors were more than just perfect conductors and provided a uniquely defining property of the superconductor state. The abili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
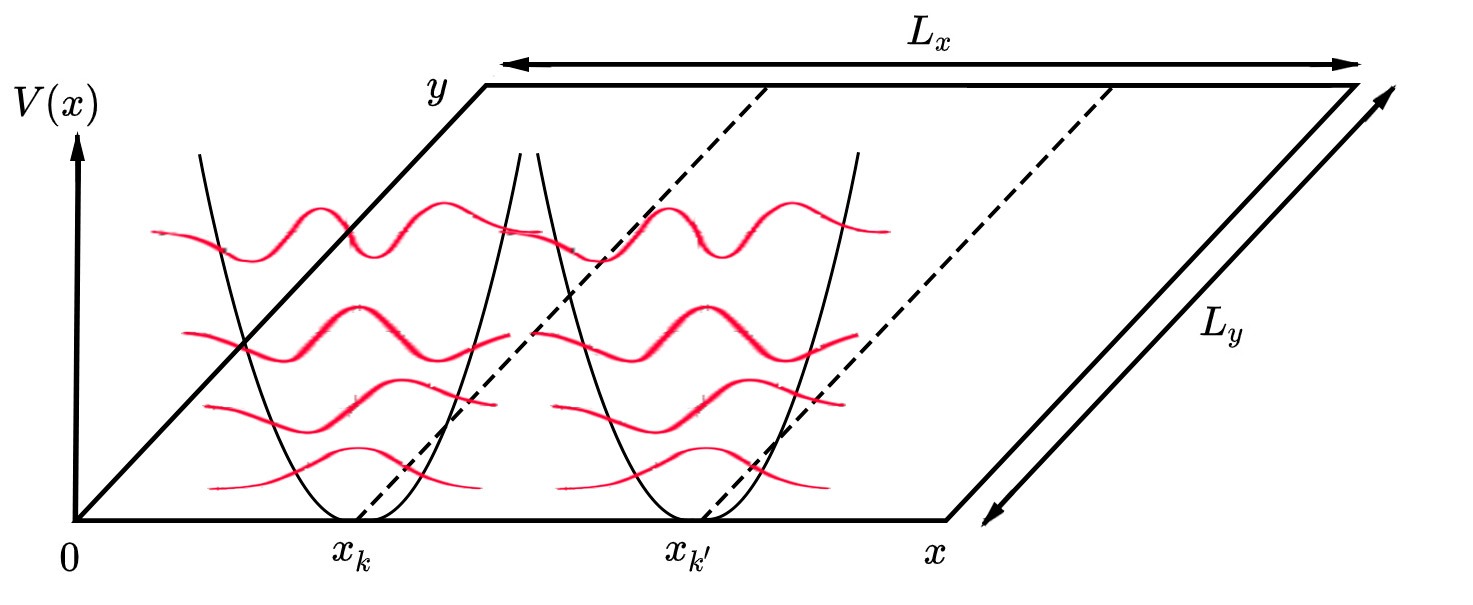



.jpg)