|
Johnson's SU-distribution
The Johnson's ''SU''-distribution is a four-parameter family of probability distributions first investigated by N. L. Johnson in 1949. Johnson proposed it as a transformation of the normal distribution: : z=\gamma+\delta \sinh^ \left(\frac\right) where z \sim \mathcal(0,1). Generation of random variables Let ''U'' be a random variable that is uniformly distributed on the unit interval , 1 Johnson's ''SU'' random variables can be generated from ''U'' as follows: : x = \lambda \sinh\left( \frac \right) + \xi where Φ is the cumulative distribution function of the normal distribution. Johnson's ''SB''-distribution N. L. Johnson firstly proposes the transformation : : z=\gamma+\delta \log \left(\frac\right) where z \sim \mathcal(0,1). Johnson's ''SB'' random variables can be generated from ''U'' as follows: : y=^ : x=\lambda y +\xi The ''SB''-distribution is convenient to Platykurtic distributions (Kurtosis). To simulate ''SU'', sample of code for its de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Investment Management
Investment management (sometimes referred to more generally as financial asset management) is the professional asset management of various Security (finance), securities, including shareholdings, Bond (finance), bonds, and other assets, such as real estate, to meet specified investment goals for the benefit of investors. Investors may be institutions, such as insurance companies, pension funds, corporations, charities, educational establishments, or private investors, either directly via investment contract, contracts/mandates or via collective investment schemes like mutual funds, exchange-traded funds, or REIT, Real estate investment trusts. The term ''investment management'' is often used to refer to the management of investment funds, most often specializing in private equity, private and public equity, real assets, alternative assets, and/or bonds. The more generic term ''asset management'' may refer to management of assets not necessarily primarily held for investment purpos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meson
In particle physics, a meson () is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, they have a meaningful physical size, a diameter of roughly one femtometre (10 m), which is about 0.6 times the size of a proton or neutron. All mesons are unstable, with the longest-lived lasting for only a few tenths of a nanosecond. Heavier mesons decay to lighter mesons and ultimately to stable electrons, neutrinos and photons. Outside the nucleus, mesons appear in nature only as short-lived products of very high-energy collisions between particles made of quarks, such as cosmic rays (high-energy protons and neutrons) and baryonic matter. Mesons are routinely produced artificially in cyclotrons or other particle accelerators in the collisions of protons, antiprotons, or other particles. Higher-energy (more massive) mesons were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant Mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, it is a characteristic of the system's total energy and momentum that is the same in all frames of reference related by Lorentz transformations.Lawrence S. LernerPhysics for Scientists and Engineers, Volume 2, page 1073 1997. If a center-of-momentum frame exists for the system, then the invariant mass of a system is equal to its total mass in that "rest frame". In other reference frames, where the system's momentum is non-zero, the total mass (a.k.a. relativistic mass) of the system is greater than the invariant mass, but the invariant mass remains unchanged. Because of mass–energy equivalence, the rest energy of the system is simply the invariant mass times the speed of light squared. Similarly, the total energy of the system is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Distribution Function
In statistics, an empirical distribution function ( an empirical cumulative distribution function, eCDF) is the Cumulative distribution function, distribution function associated with the empirical measure of a Sampling (statistics), sample. This cumulative distribution function is a step function that jumps up by at each of the data points. Its value at any specified value of the measured variable is the fraction of observations of the measured variable that are less than or equal to the specified value. The empirical distribution function is an Estimator, estimate of the cumulative distribution function that generated the points in the sample. It converges with probability 1 to that underlying distribution, according to the Glivenko–Cantelli theorem. A number of results exist to quantify the rate of Convergence of random variables#Convergence in distribution, convergence of the empirical distribution function to the underlying cumulative distribution function. Definition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
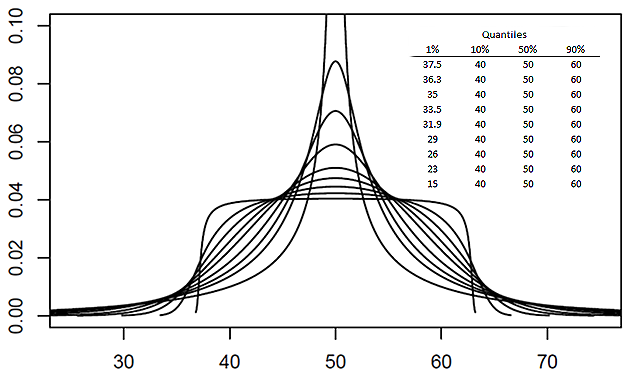
Quantile-parameterized Distribution
A quantile-parameterized distribution (QPD) is a probability distributions that is directly parameterized by data. They were created to meet the need for easy-to-use continuous probability distributions flexible enough to represent a wide range of uncertainties, such as those commonly encountered in business, economics, engineering, and science. Because QPDs are directly parameterized by data, they have the practical advantage of avoiding the intermediate step of Estimation theory, parameter estimation, a time-consuming process that typically requires non-linear iterative methods to estimate probability-distribution parameters from data. Some QPDs have virtually unlimited shape flexibility and closed-form moments as well. History The development of quantile-parameterized distributions was inspired by the practical need for flexible continuous probability distributions that are easy to fit to data. Historically, the Pearson distribution, Pearson and Norman Lloyd Johnson, Johnson fam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Binomial Tree
In quantitative finance, a lattice model is a numerical approach to the valuation of derivatives in situations requiring a discrete time model. For dividend paying equity options, a typical application would correspond to the pricing of an American-style option, where a decision to exercise is allowed at the closing of any calendar day up to the maturity. A continuous model, on the other hand, such as the standard Black–Scholes one, would only allow for the valuation of European options, where exercise is limited to the option's maturity date. For interest rate derivatives lattices are additionally useful in that they address many of the issues encountered with continuous models, such as pull to par. The method is also used for valuing certain exotic options, because of path dependence in the payoff. Traditional Monte Carlo methods for option pricing fail to account for optimal decisions to terminate the derivative by early exercise, but some methods now exist for solvin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility Smile
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Option Pricing
In finance, a price (premium) is paid or received for purchasing or selling options. The calculation of this premium will require sophisticated mathematics. Premium components This price can be split into two components: intrinsic value, and time value (also called "extrinsic value"). Intrinsic value The ''intrinsic value'' is the difference between the underlying spot price and the strike price, to the extent that this is in favor of the option holder. For a call option, the option is in-the-money if the underlying spot price is higher than the strike price; then the intrinsic value is the underlying price minus the strike price. For a put option, the option is in-the-money if the ''strike'' price is higher than the underlying spot price; then the intrinsic value is the strike price minus the underlying spot price. Otherwise the intrinsic value is zero. For example, when a DJI call (bullish/long) option is 18,000 and the underlying DJI Index is priced at $18,050 then there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and Data and information visualization, data visualization. It has been widely adopted in the fields of data mining, bioinformatics, data analysis, and data science. The core R language is extended by a large number of R package, software packages, which contain Reusability, reusable code, documentation, and sample data. Some of the most popular R packages are in the tidyverse collection, which enhances functionality for visualizing, transforming, and modelling data, as well as improves the ease of programming (according to the authors and users). R is free and open-source software distributed under the GNU General Public License. The language is implemented primarily in C (programming language), C, Fortran, and Self-hosting (compilers), R itself. Preprocessor, Precompiled executables are available for the major operating systems (including Linux, MacOS, and Microsoft Windows). Its core is an interpreted language with a na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |