|
Isosceles Triangle
In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The two equal sides are called the legs and the third side is called the base of the triangle. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by simple formulas from the lengths of the legs an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-Collinearity, collinear, determine a unique triangle and simultaneously, a unique Plane (mathematics), plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved new innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus (mathematician), Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the philosophers Proclus and Pappus of Alexandria many centuries later. Until the early Renaissance he was often mistaken f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
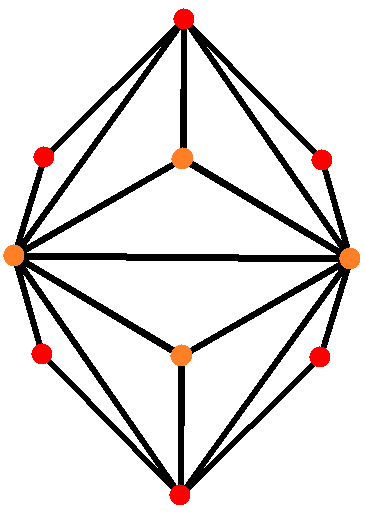
Triakis Octahedron
In geometry, a triakis octahedron (or trigonal trisoctahedron or kisoctahedronConway, Symmetries of things, p. 284) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube. It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a ''trisoctahedron'', or, more fully, ''trigonal trisoctahedron''. Both names reflect that it has three triangular faces for every face of an octahedron. The ''tetragonal trisoctahedron'' is another name for the deltoidal icositetrahedron, a different polyhedron with three quadrilateral faces for every face of an octahedron. This convex polyhedron is topologically similar to the concave stellated octahedron. They have the same face connectivity, but the vertices are in different relative distances from the center. If its shorter edges have length 1, its surface area and volume are: :\begin A &= 3\sqrt \\ V &= \frac \end Cartesian coo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Tetrahedron
In geometry, a triakis tetrahedron (or kistetrahedron) is a Catalan solid with 12 faces. Each Catalan solid is the dual of an Archimedean solid. The dual of the triakis tetrahedron is the truncated tetrahedron. The triakis tetrahedron can be seen as a tetrahedron with a triangular pyramid added to each face; that is, it is the Kleetope of the tetrahedron. It is very similar to the net for the 5-cell, as the net for a tetrahedron is a triangle with other triangles added to each edge, the net for the 5-cell a tetrahedron with pyramids attached to each face. This interpretation is expressed in the name. The length of the shorter edges is that of the longer edges. If the triakis tetrahedron has shorter edge length 1, it has area and volume . Cartesian coordinates Cartesian coordinates for the 8 vertices of a triakis tetrahedron centered at the origin, are the points (±5/3, ±5/3, ±5/3) with an even number of minus signs, along with the points (±1, ±1, ±1) with an odd numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Triangular Tiling
In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex. As the name implies this tiling is constructed by a truncation operation applies to a hexagonal tiling, leaving dodecagons in place of the original hexagons, and new triangles at the original vertex locations. It is given an extended Schläfli symbol of ''t''. Conway calls it a truncated hextille, constructed as a truncation operation applied to a hexagonal tiling (hextille). There are 3 regular and 8 semiregular tilings in the plane. Uniform colorings There is only one uniform coloring of a truncated hexagonal tiling. (Naming the colors by indices around a vertex: 122.) Topologically identical tilings The dodecagonal faces can be distorted into different geometries, such as: Related polyhedra and tilings Wythoff constructions from hexagonal and triangular tilings Like the uniform polyhedra there are eight ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calabi Triangle
The Calabi triangle is a special triangle found by Eugenio Calabi and defined by its property of having three different placements for the largest square that it contains. It is an obtuse isosceles triangle with an irrational but algebraic ratio between the lengths of its sides and its base. Definition Consider the largest square that can be placed in an arbitrary triangle. It may be that such a square could be positioned in the triangle in more than one way. If the largest such square can be positioned in three different ways, then the triangle is either an equilateral triangle or the Calabi triangle. Thus, the Calabi triangle may be defined as a triangle that is not equilateral and has three placements for its largest square. Shape The Calabi triangle is isosceles. The ratio of the base to either leg is : x = \Bigg(1 + \sqrt + \sqrt \Bigg) = 1.55138752454...\,. This value can also be expressed without complex numbers by using trigonometric functions: : x = \bigg(1 + \sqrt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Right Triangle
A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of Natural number, whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometry, geometric problems without resorting to more advanced methods. Angle-based "Angle-based" special right triangles are specified by the relationships of the angles of which the triangle is composed. The angles of these triangles are such that the larger (right) angle, which is 90 degree (angle), degrees or radians, is e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apex (geometry)
In geometry, an apex (plural apices) is the vertex which is in some sense the "highest" of the figure to which it belongs. The term is typically used to refer to the vertex opposite from some " base". The word is derived from the Latin for 'summit, peak, tip, top, extreme end'. Isosceles triangles In an isosceles triangle In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter versio ..., the apex is the vertex where the two sides of equal length meet, opposite the unequal third side. Pyramids and cones In a Pyramid (geometry), pyramid or Cone (geometry), cone, the apex is the vertex at the "top" (opposite the base). In a pyramid, the vertex is the point that is part of all the lateral faces, or where all the lateral edges meet. References {{elementary-geometry-stub Parts of a triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base (geometry)
In geometry, a base is a side of a polygon or a face of a polyhedron, particularly one oriented perpendicular to the direction in which height is measured, or on what is considered to be the "bottom" of the figure. This term is commonly applied to triangles, parallelograms, trapezoids, cylinders, cones, pyramids, parallelepipeds and frustums. Role in area and volume calculation Bases are commonly used (together with heights) to calculate the areas and volumes of figures. In speaking about these processes, the measure (length or area) of a figure's base is often referred to as its "base." By this usage, the area of a parallelogram or the volume of a prism or cylinder can be calculated by multiplying its "base" by its height; likewise, the areas of triangles and the volumes of cones and pyramids are fractions of the products of their bases and heights. Some figures have two parallel bases (such as trapezoids and frustums), both of which are used to calculate the extent of the figu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leg (geometry)
In a right triangle, a cathetus (originally from the Greek word ; plural: catheti), commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called a "side about the right angle". The side opposite the right angle is the hypotenuse. In the context of the hypotenuse, the catheti are sometimes referred to simply as "the other two sides". If the catheti of a right triangle have equal lengths, the triangle is isosceles. If they have different lengths, a distinction can be made between the minor (shorter) and major (longer) cathetus. The ratio of the lengths of the catheti defines the trigonometric functions tangent and cotangent of the acute angles in the triangle: the ratio c_1/c_2 is the tangent of the acute angle adjacent to c_2 and is also the cotangent of the acute angle adjacent to c_1. In a right triangle, the length of a cathetus is the geometric mean of the length of the adjacent segment cut by the altitude to the hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Set
In discrete geometry, an isosceles set is a set of points with the property that every three of them form an isosceles triangle. More precisely, each three points should determine at most two distances; this also allows degenerate isosceles triangles formed by three equally-spaced points on a line. History The problem of finding the largest isosceles set in a Euclidean space of a given dimension was posed in 1946 by Paul Erdős. In his statement of the problem, Erdős observed that the largest such set in the Euclidean plane has six points. In his 1947 solution, Leroy Milton Kelly showed more strongly that the unique six-point planar isosceles set consists of the vertices and center of a regular pentagon. In three dimensions, Kelly found an eight-point isosceles set, six points of which are the same; the remaining two points lie on a line perpendicular to the pentagon through its center, at the same distance as the pentagon vertices from the center. This three-dimensional example wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Trapezoid
In Euclidean geometry, an isosceles trapezoid (isosceles trapezium in British English) is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal length (properties shared with the parallelogram). The diagonals are also of equal length. The base angles of an isosceles trapezoid are equal in measure (there are in fact two pairs of equal base angles, where one base angle is the supplementary angle of a base angle at the other base). Special cases Rectangles and squares are usually considered to be special cases of isosceles trapezoids though s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |