|
Integral Of Secant Cubed
The integral of secant cubed is a frequent and challenging indefinite integral of elementary calculus: :\begin \int \sec^3 x \, dx &= \tfrac12\sec x \tan x + \tfrac12 \int \sec x\, dx + C \\ mu&= \tfrac12(\sec x \tan x + \ln \left, \sec x + \tan x\) + C \\ mu&= \tfrac12(\sec x \tan x + \operatorname^ x) + C, \qquad , x, < \tfrac12\pi \end where is the inverse , the . There are a number of reasons why this particular antiderivative is worthy of special attention: * The technique used for reducing integrals of higher odd powers of secant to lower ones is fully present in this, the simpl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
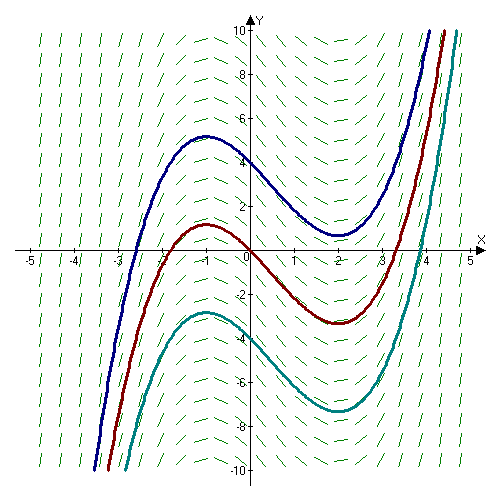
Indefinite Integral
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, velocity and accelera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus and integral calculus; the former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus, and they make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. Infinitesimal calculus was developed independently in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Later work, including (ε, δ)-definition of limit, codify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
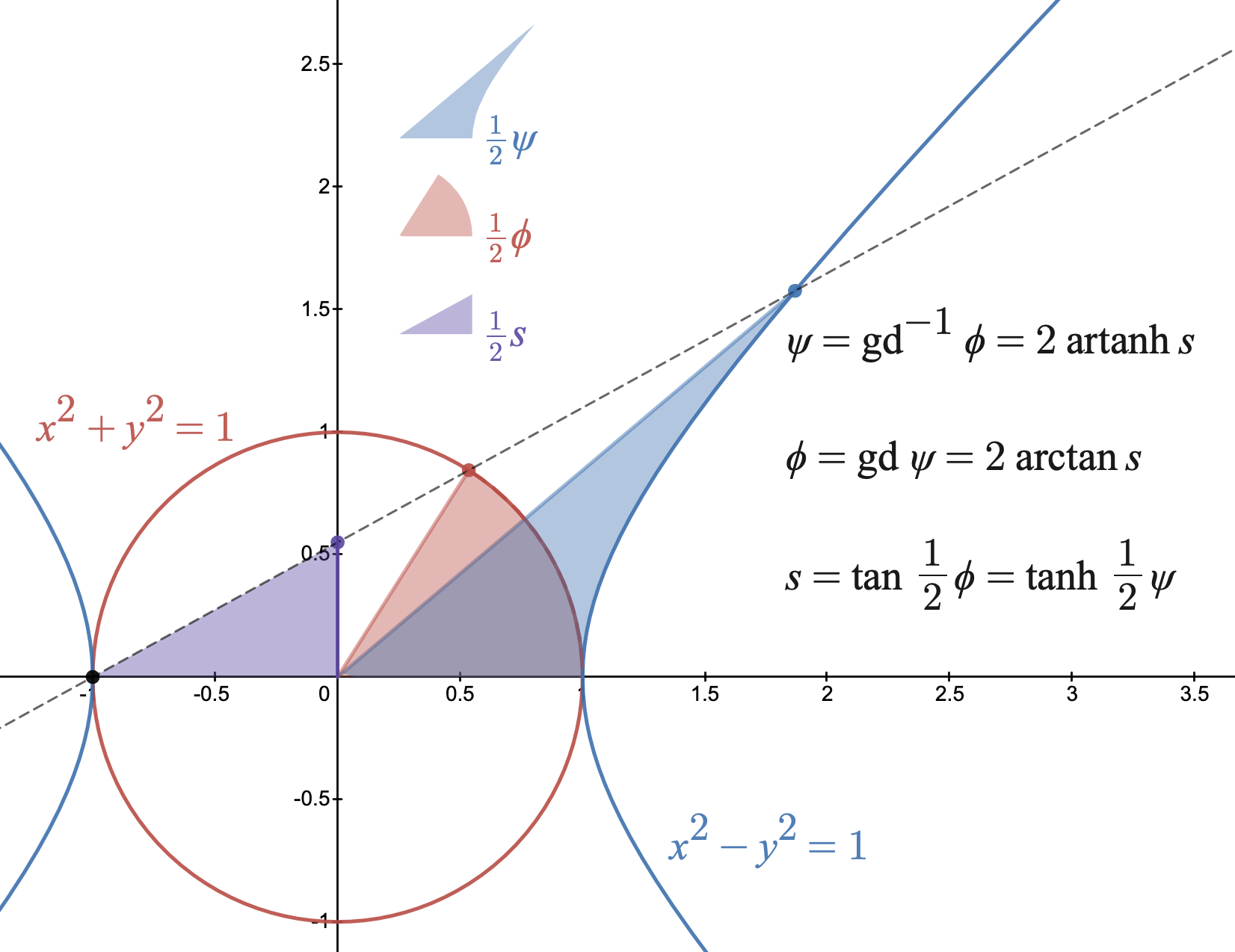
Gudermannian Function
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant The real inverse Gudermannian function can be defined for as the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Of The Secant Function
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities, : \int \sec \theta \, d\theta = \begin \dfrac12 \ln \left, \dfrac\ + C \\ 5pt\ln\left, \sec\theta + \tan\theta\ + C \\ 5pt\ln\left, \tan\left(\dfrac + \dfrac\right) \ + C\\ 5pt\end This formula is useful for evaluating various trigonometric integrals. In particular, it can be used to evaluate the integral of the secant cubed, which, though seemingly special, comes up rather frequently in applications. Proof that the different antiderivatives are equivalent Trigonometric forms : \int \sec \theta \, d\theta = \left\\text The second of these follows by first multiplying top and bottom of the interior fraction by . This gives in the denominator, and the result follows by moving the factor of into the logarithm as a square root. Leaving out the const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrating By Parts
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation. The integration by parts formula states: \begin \int_a^b u(x) v'(x) \, dx & = \Big (x) v(x)\Biga^b - \int_a^b u'(x) v(x) \, dx\\ & = u(b) v(b) - u(a) v(a) - \int_a^b u'(x) v(x) \, dx. \end Or, letting u = u(x) and du = u'(x) \,dx while v = v(x) and dv = v'(x) \, dx, the formula can be written more compactly: \int u \, dv \ =\ uv - \int v \, du. Mathematician Brook Taylor discovered integration by parts, first publishing the idea in 1715. More general formulations of integration by parts exi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services * Airport Regions Conference, a European organization of major airports * Amalgamated Roadstone Corporation, a British stone quarrying company * American Record Company (1904–1908, re-activated 1979), one of two United States record labels by this name * American Record Corporation (1929–1938), a United States record label also known as American Record Company * ARC (American Recording Company) (1978-present), a vanity label for Earth, Wind & Fire * ARC Document Solutions, a company based in California, formerly American Reprographics Company * Amey Roadstone Construction, a former British construction company * Aqaba Railway Corporation, a freight railway in Jordan * ARC/Architectural Resources Cambridge, Inc., Cambridge, Massachusett ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point where the parabola intersects its axis of symmetry is called the "vertex" and is the point where the parabola is most sharply curved. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Spiral
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates it can be described by the equation r = a + b\cdot\theta with real numbers and . Changing the parameter moves the centerpoint of the spiral outward from the origin (positive toward and negative toward ) essentially through a rotation of the spiral, while controls the distance between loops. From the above equation, it can thus be stated: position of particle from point of start is proportional to angle as time elapses. Archimedes described such a spiral in his book '' On Spirals''. Conon of Samos was a friend of his and Pappus states that this spiral was discovered by Conon. Derivation of general equation of spiral A p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is the Minkowski cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helicoid
The helicoid, also known as helical surface, after the plane and the catenoid, is the third minimal surface to be known. Description It was described by Euler in 1774 and by Jean Baptiste Meusnier in 1776. Its name derives from its similarity to the helix: for every point on the helicoid, there is a helix contained in the helicoid which passes through that point. Since it is considered that the planar range extends through negative and positive infinity, close observation shows the appearance of two parallel or mirror planes in the sense that if the slope of one plane is traced, the co-plane can be seen to be bypassed or skipped, though in actuality the co-plane is also traced from the opposite perspective. The helicoid is also a ruled surface (and a right conoid), meaning that it is a trace of a line. Alternatively, for any point on the surface, there is a line on the surface passing through it. Indeed, Catalan proved in 1842 that the helicoid and the plane were the only rul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other ... where the function is Riemann integrable is eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |