|
Injection Locked Oscillator
Injection locking and injection pulling are the frequency effects that can occur when a harmonic oscillator is disturbed by a second oscillator operating at a nearby frequency. When the coupling is strong enough and the frequencies near enough, the second oscillator can capture the first oscillator, causing it to have essentially identical frequency as the second. This is injection locking. When the second oscillator merely disturbs the first but does not capture it, the effect is called injection pulling. Injection locking and pulling effects are observed in numerous types of physical systems, however the terms are most often associated with electronic oscillators or laser resonators. Injection locking has been used in beneficial and clever ways in the design of early television sets and oscilloscopes, allowing the equipment to be synchronized to external signals at a relatively low cost. Injection locking has also been used in high performance frequency doubling circuits. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its Mechanical equilibrium, equilibrium position, experiences a restoring force ''F'' Proportionality (mathematics), proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive coefficient, constant. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (Damping ratio, damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the Damping ratio, undamped case, and an amplitude decreasing with time (Damping ratio, underdamped oscillator). * Decay to the equilibrium p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LC Circuit
An LC circuit, also called a resonant circuit, tank circuit, or tuned circuit, is an electric circuit consisting of an inductor, represented by the letter L, and a capacitor, represented by the letter C, connected together. The circuit can act as an electrical resonator, an electrical analogue of a tuning fork, storing energy oscillating at the circuit's resonant frequency. LC circuits are used either for generating signals at a particular frequency, or picking out a signal at a particular frequency from a more complex signal; this function is called a bandpass filter. They are key components in many electronic devices, particularly radio equipment, used in circuits such as oscillators, filters, tuners and frequency mixers. An LC circuit is an idealized model since it assumes there is no dissipation of energy due to resistance. Any practical implementation of an LC circuit will always include loss resulting from small but non-zero resistance within the components and conn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metronome
A metronome, from ancient Greek μέτρον (''métron'', "measure") and νομός (nomós, "custom", "melody") is a device that produces an audible click or other sound at a regular interval that can be set by the user, typically in beats per minute (BPM). Metronomes may include synchronized visual motion. Musicians use the device to practise playing to a regular pulse. A kind of metronome was among the inventions of Andalusian polymath Abbas ibn Firnas (810–887). In 1815, German inventor Johann Maelzel patented his mechanical, wind-up metronome as a tool for musicians, under the title "Instrument/Machine for the Improvement of all Musical Performance, called Metronome". In the 20th century, electronic metronomes and software metronomes were invented. Musicians practise with metronomes to improve their timing, especially the ability to stick to a regular tempo. Metronome practice helps internalize a clear sense of timing and tempo. Composers and conductors often use a me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sympathetic Resonance
Sympathetic resonance or sympathetic vibration is a harmonic phenomenon wherein a passive string or vibratory body responds to external vibrations to which it has a harmonic likeness. The classic example is demonstrated with two similarly-tuned tuning forks. When one fork is struck and held near the other, vibrations are induced in the unstruck fork, even though there is no physical contact between them. In similar fashion, strings will respond to the vibrations of a tuning fork when sufficient harmonic relations exist between them. The effect is most noticeable when the two bodies are tuned in unison or an octave apart (corresponding to the first and second harmonics, integer multiples of the inducing frequency), as there is the greatest similarity in vibrational frequency. Sympathetic resonance is an example of injection locking occurring between coupled oscillators, in this case coupled through vibrating air. In musical instruments, sympathetic resonance can produce both desi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Oscillators
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive constant. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the undamped case, and an amplitude decreasing with time (underdamped oscillator). * Decay to the equilibrium position, without oscillations (overdamped oscillator). The boundary solution between an underdamped oscillato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
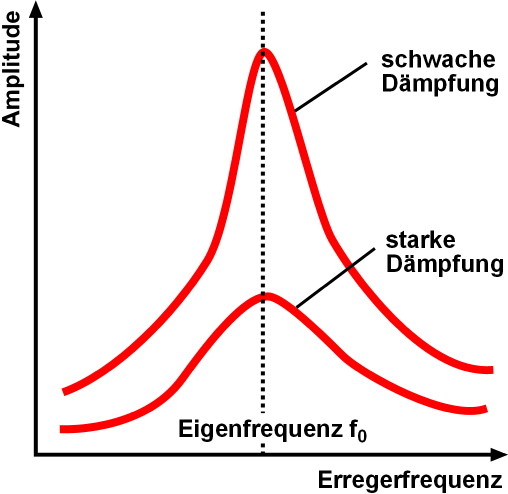
Resonant
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and reson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and reso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Feedback
Negative feedback (or balancing feedback) occurs when some function (Mathematics), function of the output of a system, process, or mechanism is feedback, fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. Whereas positive feedback tends to lead to instability via exponential growth, oscillation or chaos theory, chaotic behavior, negative feedback generally promotes stability. Negative feedback tends to promote a settling to List of types of equilibrium, equilibrium, and reduces the effects of perturbations. Negative feedback loops in which just the right amount of correction is applied with optimum timing can be very stable, accurate, and responsive. Negative feedback is widely used in mechanical and electronic engineering, and also within living organisms, and can be seen in many other fields from chemistry and economics to physical systems such as the climate. General negative feedback ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Out Of Phase
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \phi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \phi(t) is also a periodic function, with the same period as F, that repeatedly scans the same range of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synchronization
Synchronization is the coordination of events to operate a system in unison. For example, the conductor of an orchestra keeps the orchestra synchronized or ''in time''. Systems that operate with all parts in synchrony are said to be synchronous or ''in sync''—and those that are not are '' asynchronous''. Today, time synchronization can occur between systems around the world through satellite navigation signals and other time and frequency transfer techniques. Navigation and railways Time-keeping and synchronization of clocks is a critical problem in long-distance ocean navigation. Before radio navigation and satellite-based navigation, navigators required accurate time in conjunction with astronomical observations to determine how far east or west their vessel traveled. The invention of an accurate marine chronometer revolutionized marine navigation. By the end of the 19th century, important ports provided time signals in the form of a signal gun, flag, or dropping time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |