|
Information Engineering (field)
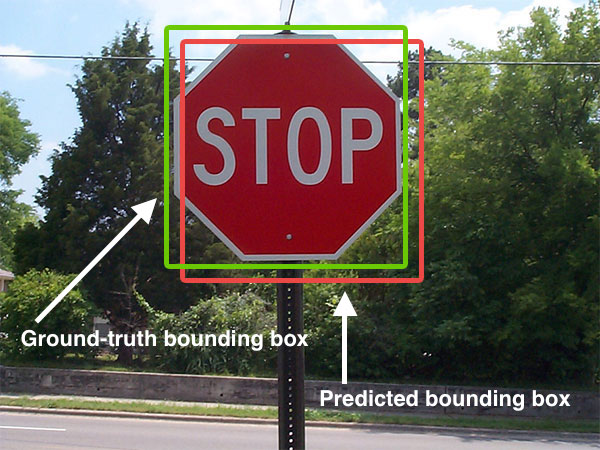
Information engineering is the engineering discipline that deals with the generation, distribution, analysis, and use of information, data, and knowledge in systems. The field first became identifiable in the early 21st century. The components of information engineering include more theoretical fields such as machine learning, artificial intelligence, control theory, signal processing, and information theory, and more applied fields such as computer vision, natural language processing, bioinformatics, medical image computing, cheminformatics, autonomous robotics, mobile robotics, and telecommunications. Many of these originate from computer science, as well as other branches of engineering such as computer engineering, electrical engineering, and bioengineering. The field of information engineering is based heavily on mathematics, particularly probability, statistics, calculus, linear algebra, optimization, differential equations, variational calculus, and complex analysis. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knowledge
Knowledge can be defined as awareness of facts or as practical skills, and may also refer to familiarity with objects or situations. Knowledge of facts, also called propositional knowledge, is often defined as true belief that is distinct from opinion or guesswork by virtue of justification. While there is wide agreement among philosophers that propositional knowledge is a form of true belief, many controversies in philosophy focus on justification: whether it is needed at all, how to understand it, and whether something else besides it is needed. These controversies intensified due to a series of thought experiments by Edmund Gettier and have provoked various alternative definitions. Some of them deny that justification is necessary and replace it, for example, with reliability or the manifestation of cognitive virtues. Others contend that justification is needed but formulate additional requirements, for example, that no defeaters of the belief are present or that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bioengineering
Biological engineering or bioengineering is the application of principles of biology and the tools of engineering to create usable, tangible, economically-viable products. Biological engineering employs knowledge and expertise from a number of pure and applied sciences, such as mass and heat transfer, kinetics, biocatalysts, biomechanics, bioinformatics, separation and purification processes, bioreactor design, surface science, fluid mechanics, thermodynamics, and polymer science. It is used in the design of medical devices, diagnostic equipment, biocompatible materials, renewable energy, ecological engineering, agricultural engineering, process engineering and catalysis, and other areas that improve the living standards of societies. Examples of bioengineering research include bacteria engineered to produce chemicals, new medical imaging technology, portable and rapid disease diagnostic devices, prosthetics, biopharmaceuticals, and tissue-engineered organs. Bioengineering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Industry (economics)
In macroeconomics, an industry is a branch of an economy that Production (economics) , produces a closely-related set of raw materials, Good (economics) , goods, or Service (economics) , services. For example, one might refer to the wood industry or to the insurance industry. When evaluating a single group or company, its dominant source of revenue is typically used by industry classifications to classify it within a specific industry. For example the International Standard Industrial Classification (ISIC) – used directly or through derived classifications for the official statistics of most countries worldwide – classifies "statistical units" by the "economic activity in which they mainly engage". Industry is then defined as "set of statistical units that are classified into the same ISIC category". However, a single business need not belong just to one industry, such as when a large business (often referred to as a conglomerate (company), conglomerate) Diversification (m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Institute Of Measurement And Control
Founded in 1944 and incorporated by Royal Charter in 1975, The Institute of Measurement and Control (InstMC) is a professional members institution for individuals and companies that operate within the measurement and control industries. Its aims are to advance the science and practice of measurement and control technologies and their various applications, to foster the exchange of views and the communication of knowledge and ideas in these activities, and to promote the professional qualification and standing of its members. The institute is both a learned society and a professional qualifying body. InstMC is registered with the Engineering Council and is one of the licensed member institutions allowed to register Chartered Engineers (CEng) The institute is the UK member body of the International Measurement Confederation (IMEKO) and is the secretariat to the United Kingdom Automatic Control Council (UKACC). Special Interest Groups This Institute currently has range of Special ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Institution Of Engineering And Technology
The Institution of Engineering and Technology (IET) is a multidisciplinary professional engineering institution. The IET was formed in 2006 from two separate institutions: the Institution of Electrical Engineers (IEE), dating back to 1871, and the Institution of Incorporated Engineers (IIE) dating back to 1884. Its worldwide membership is currently in excess of 158,000 in 153 countries. The IET's main offices are in Savoy Place in London, England, and at Michael Faraday House in Stevenage, England. In the United Kingdom, the IET has the authority to establish professional registration for the titles of Chartered Engineer, Incorporated Engineer, Engineering Technician, and ICT Technician, as a licensed member institution of the Engineering Council. The IET is registered as a charity in England and Wales, and in Scotland. Formation Discussions started in 2004 between the IEE and the IIE about merging to form a new institution. In September 2005, both institutions held votes o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Professional Body
A professional association (also called a professional body, professional organization, or professional society) usually seeks to further a particular profession, the interests of individuals and organisations engaged in that profession, and the public interest. In the United States, such an association is typically a nonprofit business league for tax purposes. Roles The roles of professional associations have been variously defined: "A group, of people in a learned occupation who are entrusted with maintaining control or oversight of the legitimate practice of the occupation;" also a body acting "to safeguard the public interest;" organizations which "represent the interest of the professional practitioners," and so "act to maintain their own privileged and powerful position as a controlling body." Professional associations are ill defined although often have commonality in purpose and activities. In the UK, the Science Council defines a professional body as "an organisation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Academic Degree
An academic degree is a qualification awarded to students upon successful completion of a course of study in higher education, usually at a college or university. These institutions commonly offer degrees at various levels, usually including undergraduate degrees, master's, and doctorates, often alongside other academic certificates and professional degrees. The most common undergraduate degree is the bachelor's degree, although in some countries there are lower level higher education qualifications that are also titled degrees (e.g. associate degrees and foundation degrees). History Emergence of the doctor's and master's degrees and the licentiate The doctorate ( Latin: ''doceo'' "I teach") appeared in medieval Europe as a license to teach ( Latin: ''licentia docendi'') at a medieval university. Its roots can be traced to the early church when the term "doctor" referred to the Apostles, church fathers and other Christian authorities who taught and interpreted the B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable (that is, holomorphic functions). History Complex analysis is one of the classical branches in mathematics, with roots in the 18th century and just prior. Important mathematicians associated with comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Calculus
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends upon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equations
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, optimization includes finding "best available" values of some objective function given a def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as: :a_1x_1+\cdots +a_nx_n=b, linear maps such as: :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to spaces of functions. Linear algebra is also used in most sciences and fields of engineering, because it allows modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order approximations, using the fact that the differential of a multivariate function at a point is the line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |