|
Improper Rotation
In geometry, an improper rotation. (also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion) is an isometry in Euclidean space that is a combination of a Rotation (geometry), rotation about an axis and a reflection (mathematics), reflection in a plane perpendicular to that axis. Reflection and Point reflection, inversion are each a special case of improper rotation. Any improper rotation is an affine transformation and, in cases that keep the coordinate origin fixed, a linear transformation.. It is used as a symmetry operation in the context of Symmetry (geometry), geometric symmetry, molecular symmetry and Crystallographic point group, crystallography, where an object that is unchanged by a combination of rotation and reflection is said to have ''improper rotation symmetry''. Three dimensions In 3 dimensions, improper rotation is equivalently defined as a combination of rotation about an axis and inversion in a point on the axis. For this reason ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Antiprism
In geometry, the square antiprism is the second in an infinite family of antiprisms formed by an even number, even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an ''anticube''. If all its faces are regular polygon, regular, it is a semiregular polyhedron or uniform polyhedron. A nonuniform ''D''4-symmetric variant is the cell of the Noble polyhedron, noble square antiprismatic 72-cell. Points on a sphere When eight points are distributed on the surface of a sphere with the aim of maximising the distance between them in some sense, the resulting shape corresponds to a square antiprism rather than a cube (geometry), cube. Specific methods of distributing the points include, for example, the Thomson problem (minimizing the sum of all the reciprocal (mathematics), reciprocals of distances between points), maximising the distance of each point to the nearest point, or minimising the sum of all reciprocals of squares of distances between points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \mathrm_n defined over a finite set of n symbols consists of the permutations that can be performed on the n symbols. Since there are n! (n factorial) such permutation operations, the order (number of elements) of the symmetric group \mathrm_n is n!. Although symmetric groups can be defined on infinite sets, this article focuses on the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mirror
A mirror, also known as a looking glass, is an object that Reflection (physics), reflects an image. Light that bounces off a mirror forms an image of whatever is in front of it, which is then focused through the lens of the eye or a camera. Mirrors reverse the direction of light at an angle equal to its incidence. This allows the viewer to see themselves or objects behind them, or even objects that are at an angle from them but out of their field of view, such as around a corner. Natural mirrors have existed since Prehistory, prehistoric times, such as the surface of water, but people have been manufacturing mirrors out of a variety of materials for thousands of years, like stone, metals, and glass. In modern mirrors, metals like silver or aluminium are often used due to their high reflectivity, applied as a thin coating on glass because of its naturally smooth and very Hardness (materials science), hard surface. A mirror is a Wave (physics), wave reflector. Light consists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schoenflies Notation
The Schoenflies (or Schönflies) notation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the symmetry of a molecule, the notation is often sufficient and commonly used for spectroscopy. However, in crystallography, there is additional translational symmetry, and point groups are not enough to describe the full symmetry of crystals, so the full space group is usually used instead. The naming of full space groups usually follows another common convention, the Hermann–Mauguin notation, also known as the international notation. Although Schoenflies notation without superscripts is a pure point group notation, optionally, superscripts can be added to further specify individual space groups. However, for space groups, the connection to the underlying symmetry elements is much more clear in Hermann–Mauguin notation, so the latter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mirror Image
A mirror image (in a plane mirror) is a reflection (physics), reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical phenomenon, optical effect, it results from specular reflection off from surfaces of lustrous materials, especially a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3D structures. In geometry and geometrical optics In two dimensions In geometry, the mirror image of an object or 2D geometric model, two-dimensional figure is the virtual image formed by reflection (mathematics), reflection in a plane mirror; it is of the same size as the original object, yet different, unless the object or figure has reflection symmetry (also known as a P-symmetry). Two-dimensional mirror images can be seen in the reflections of mirrors or other reflecting surfaces, or on a printed surface seen inside-out. If we first look at an obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Points Of Isometry Groups In Euclidean Space
A fixed point of an isometry group is a point that is a fixed point for every isometry in the group. For any isometry group in Euclidean space the set of fixed points is either empty or an affine space. For an object, any unique centre and, more generally, any point with unique properties with respect to the object is a fixed point of its symmetry group. In particular this applies for the centroid of a figure, if it exists. In the case of a physical body, if for the symmetry not only the shape but also the density is taken into account, it applies to the centre of mass. If the set of fixed points of the symmetry group of an object is a singleton then the object has a specific centre of symmetry. The centroid and centre of mass, if defined, are this point. Another meaning of "centre of symmetry" is a point with respect to which inversion symmetry applies. Such a point needs not be unique; if it is not, there is translational symmetry, hence there are infinitely many of such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Of Rotation
The angular displacement (symbol θ, , or φ) – also called angle of rotation, rotational displacement, or rotary displacement – of a physical body is the angle (in units of radians, degrees, turns, etc.) through which the body rotates (revolves or spins) around a centre or axis of rotation. Angular displacement may be signed, indicating the sense of rotation (e.g., clockwise); it may also be greater (in absolute value) than a full turn. Context When a body rotates about its axis, the motion cannot simply be analyzed as a particle, as in circular motion it undergoes a changing velocity and acceleration at any time. When dealing with the rotation of a body, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the body's motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is mini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversion In A Point
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point is reflected across a designated inversion center, which remains fixed. In Euclidean or pseudo-Euclidean spaces, a point reflection is an isometry (preserves distance). In the Euclidean plane, a point reflection is the same as a half-turn rotation (180° or radians), while in three-dimensional Euclidean space a point reflection is an improper rotation which preserves distances but reverses orientation. A point reflection is an involution: applying it twice is the identity transformation. An object that is invariant under a point reflection is said to possess point symmetry (also called inversion symmetry or central symmetry). A point group including a point reflection among its symmetries is called ''centrosymmetric''. Inversion symmetry is found in many crystal structures and molecules, and has a major effect upon their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
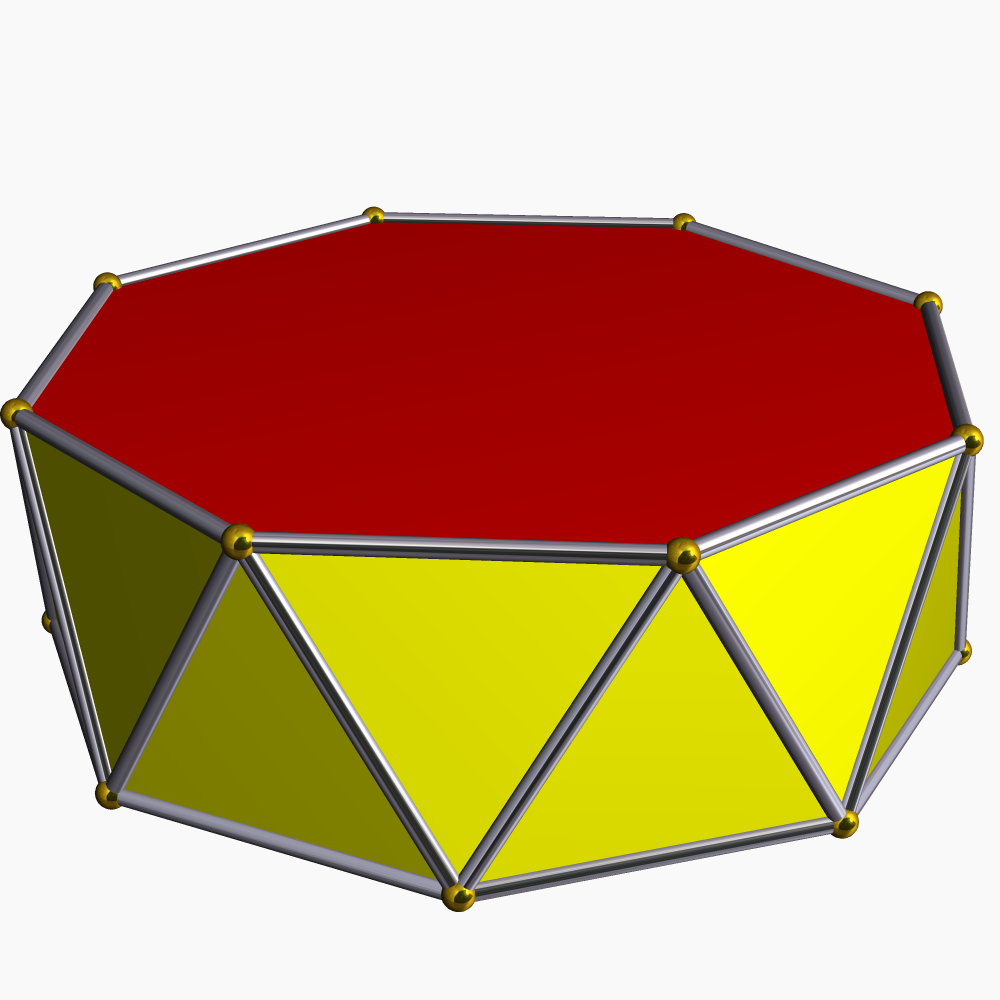
Hexagonal Antiprism
In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. Antiprisms are similar to prism (geometry), prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals. In the case of a regular ''n''-sided base, one usually considers the case where its copy is twisted by an angle . Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two bases and, connecting those bases, isosceles triangles. If faces are all regular, it is a semiregular polyhedron. Crossed antiprism A crossed hexagonal antiprism is a star polyhedron, topologically identical to the convex ''hexagonal antiprism'' with the same vertex arrangement, but it can't be made uniform; the sides are isosceles triangles. Its vertex configuration is 3.3/2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |