|
Hilbert Scheme
In algebraic geometry, a branch of mathematics, a Hilbert scheme is a scheme that is the parameter space for the closed subschemes of some projective space (or a more general projective scheme), refining the Chow variety. The Hilbert scheme is a disjoint union of projective subschemes corresponding to Hilbert polynomials. The basic theory of Hilbert schemes was developed by . Hironaka's example shows that non-projective varieties need not have Hilbert schemes. Hilbert scheme of projective space The Hilbert scheme \mathbf(n) of \mathbb^n classifies closed subschemes of projective space in the following sense: For any locally Noetherian scheme , the set of -valued points :\operatorname(S, \mathbf(n)) of the Hilbert scheme is naturally isomorphic to the set of closed subschemes of \mathbb^n \times S that are flat over . The closed subschemes of \mathbb^n \times S that are flat over can informally be thought of as the families of subschemes of projective space parameterized b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects. The fundamental objects of study in algebraic geometry are algebraic variety, algebraic varieties, which are geometric manifestations of solution set, solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are line (geometry), lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscate of Bernoulli, lemniscates and Cassini ovals. These are plane algebraic curves. A point of the plane lies on an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of points of special interest like singular point of a curve, singular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mark Haiman
Mark David Haiman is a mathematician at the University of California at Berkeley who proved the Macdonald positivity conjecture for Macdonald polynomials. He received his Ph.D. in 1984 in the Massachusetts Institute of Technology under the direction of Gian-Carlo Rota. Previous to his appointment at Berkeley, he held positions at the University of California, San Diego and the Massachusetts Institute of Technology. In 2004, he received the inaugural AMS Moore Prize. In 2012, he became a fellow of the American Mathematical Society. retrieved 2013-01-19. Selected publications *References External links * Haiman'[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quot Scheme
In algebraic geometry, the Quot scheme is a scheme parametrizing sheaves on a projective scheme. More specifically, if ''X'' is a projective scheme over a Noetherian scheme ''S'' and if ''F'' is a coherent sheaf on ''X'', then there is a scheme \operatorname_F(X) whose set of ''T''-points \operatorname_F(X)(T) = \operatorname_S(T, \operatorname_F(X)) is the set of isomorphism classes of the quotients of F \times_S T that are flat over ''T''. The notion was introduced by Alexander Grothendieck. It is typically used to construct another scheme parametrizing geometric objects that are of interest such as a Hilbert scheme. (In fact, taking ''F'' to be the structure sheaf \mathcal_X gives a Hilbert scheme.) Definition For a scheme of finite type X \to S over a Noetherian base scheme S, and a coherent sheaf \mathcal \in \text(X), there is a functor\mathcal_: (Sch/S)^ \to \textsending T \to S to\mathcal_(T) = \left\/ \simwhere X_T = X\times_ST and \mathcal_T = pr_X^*\mathcal under the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kummer Surface
In algebraic geometry, a Kummer quartic surface, first studied by , is an irreducible nodal surface of degree 4 in \mathbb^3 with the maximal possible number of 16 double points. Any such surface is the Kummer variety of the Jacobian variety of a smooth hyperelliptic curve of genus 2; i.e. a quotient of the Jacobian by the Kummer involution ''x'' ↦ −''x''. The Kummer involution has 16 fixed points: the 16 2-torsion point of the Jacobian, and they are the 16 singular points of the quartic surface. Resolving the 16 double points of the quotient of a (possibly nonalgebraic) torus by the Kummer involution gives a K3 surface with 16 disjoint rational curves; these K3 surfaces are also sometimes called Kummer surfaces. Other surfaces closely related to Kummer surfaces include Weddle surfaces, wave surfaces, and tetrahedroids. Geometry Singular quartic surfaces and the double plane model Let K\subset\mathbb^3 be a quartic surface with an ordinary double ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperkähler Manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold (M, g) endowed with three integrable almost complex structures I, J, K that are Kähler with respect to the Riemannian metric g and satisfy the quaternionic relations I^2=J^2=K^2=IJK=-1. In particular, it is a hypercomplex manifold. All hyperkähler manifolds are Ricci-flat and are thus Calabi–Yau manifolds. Hyperkähler manifolds were first given this name by Eugenio Calabi in 1979. Early history Marcel Berger's 1955 paper on the classification of Riemannian holonomy groups first raised the issue of the existence of non-symmetric manifolds with holonomy Sp(''n'')·Sp(1). Interesting results were proved in the mid-1960s in pioneering work by Edmond Bonan and Kraines who have independently proven that any such manifold admits a parallel 4-form \Omega. Bonan's later results include a Lefschetz-type result: wedging with this powers of this 4-form induces isomorphisms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calabi Conjecture
In the mathematical field of differential geometry, the Calabi conjecture was a conjecture about the existence of certain kinds of Riemannian metrics on certain complex manifolds, made by . It was proved by , who received the Fields Medal and Oswald Veblen Prize in part for his proof. His work, principally an analysis of an elliptic partial differential equation known as the complex Monge–Ampère equation, was an influential early result in the field of geometric analysis. More precisely, Calabi's conjecture asserts the resolution of the prescribed Ricci curvature problem within the setting of Kähler metrics on closed complex manifolds. According to Chern–Weil theory, the Ricci form of any such metric is a closed differential 2-form which represents the first Chern class. Calabi conjectured that for any such differential form , there is exactly one Kähler metric in each Kähler class whose Ricci form is . (Some compact complex manifolds admit no Kähler classes, in w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperkähler Manifold
In differential geometry, a hyperkähler manifold is a Riemannian manifold (M, g) endowed with three integrable almost complex structures I, J, K that are Kähler with respect to the Riemannian metric g and satisfy the quaternionic relations I^2=J^2=K^2=IJK=-1. In particular, it is a hypercomplex manifold. All hyperkähler manifolds are Ricci-flat and are thus Calabi–Yau manifolds. Hyperkähler manifolds were first given this name by Eugenio Calabi in 1979. Early history Marcel Berger's 1955 paper on the classification of Riemannian holonomy groups first raised the issue of the existence of non-symmetric manifolds with holonomy Sp(''n'')·Sp(1). Interesting results were proved in the mid-1960s in pioneering work by Edmond Bonan and Kraines who have independently proven that any such manifold admits a parallel 4-form \Omega. Bonan's later results include a Lefschetz-type result: wedging with this powers of this 4-form induces isomorphisms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hartogs' Principle
In the theory of functions of several complex variables, Hartogs's extension theorem is a statement about the singularities of holomorphic functions of several variables. Informally, it states that the support of the singularities of such functions cannot be compact, therefore the singular set of a function of several complex variables must (loosely speaking) 'go off to infinity' in some direction. More precisely, it shows that an isolated singularity is always a removable singularity for any analytic function of complex variables. A first version of this theorem was proved by Friedrich Hartogs,See the original paper of and its description in various historical surveys by , and . In particular, in this last reference on p. 132, the Author explicitly writes :-"''As it is pointed out in the title of , and as the reader shall soon see, the key tool in the proof is the Cauchy integral formula''". and as such it is known also as Hartogs's lemma and Hartogs's principle: in earlier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arnaud Beauville
Arnaud Beauville (born 10 May 1947) is a French mathematician, whose research interest is algebraic geometry. Beauville earned his doctorate from Paris Diderot University in 1977, with a thesis regarding Prym varieties and the Schottky problem, under supervision of Jean-Louis Verdier. He has been a professor at the Université Paris-Sud, then Director of the Mathematics Department at the École Normale Supérieure. He is currently Professor emeritus at the Université de Nice Sophia-Antipolis. Beauville was a visiting scholar at the Institute for Advanced Study in the summer of 1982. He was an invited speaker at the International Congress of Mathematicians in 1986 at Berkeley. He was a member of Bourbaki. He has had 25 Ph.D. students, among them Claire Voisin, Olivier Debarre, Yves Laszlo. In 2012 he became a fellow of the American Mathematical Society. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Akira Fujiki
Akira may refer to: People *Akira (given name); and a list of people with this given name Surnames *Asa Akira (born 1986), American pornographic actress, model, and director *Elly Akira, Japanese pornographic actress *Francesco Akira (born 1999), Japanese ring name for Italian wrestler Francesco Begnini Mononymed people *Akira (actor) (born 1981), Japanese actor and dance performer * Akira (American wrestler) (born 1993), American professional wrestler *Akira Nogami (born 1966; ring name "AKIRA"), Japanese professional wrestler and actor *Natalie Horler (born 1981; stage name "Akira"), German singer and television presenter formerly using the stagename "Akira" * Akira the Don, stagename of British DJ Adam Narkiewicz * Akira the Hustler (born 1969), stagename of Japanese artist Yukio Cho Fictional characters *Akira Yuki, a major character of the ''Virtua Fighter'' series of video games * Akira (''The Simpsons''), a Japanese chef on ''The Simpsons'' * Akira (''Akira''), a characte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symplectic Geometry
Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry has its origins in the Hamiltonian formulation of classical mechanics where the phase space of certain classical systems takes on the structure of a symplectic manifold. The term "symplectic", introduced by Hermann Weyl, is a calque of "complex"; previously, the "symplectic group" had been called the "line complex group". "Complex" comes from the Latin ''com-plexus'', meaning "braided together" (co- + plexus), while symplectic comes from the corresponding Greek ''sym-plektikos'' (συμπλεκτικός); in both cases the stem comes from the Indo-European root *pleḱ- The name reflects the deep connections between complex and symplectic structures. By Darboux's theorem, symplectic manifolds are isomorphic to the standard symplectic vector space locally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
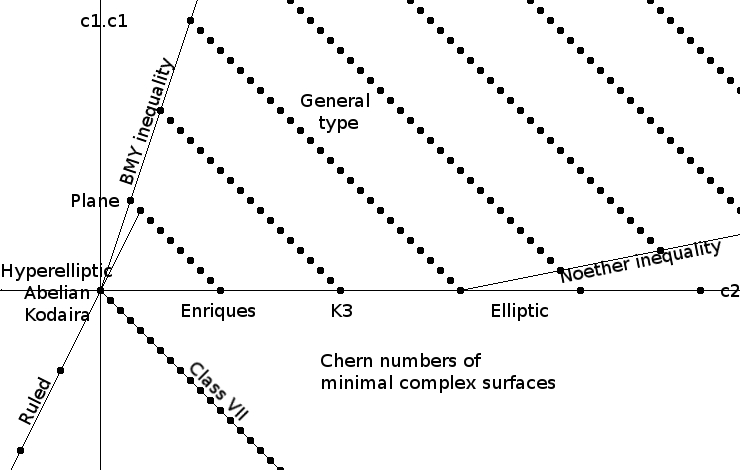
Enriques–Kodaira Classification
In mathematics, the Enriques–Kodaira classification groups compact complex surfaces into ten classes, each parametrized by a moduli space. For most of the classes the moduli spaces are well understood, but for the class of surfaces of general type the moduli spaces seem too complicated to describe explicitly, though some components are known. Max Noether began the systematic study of algebraic surfaces, and Guido Castelnuovo proved important parts of the classification. described the classification of complex projective surfaces. later extended the classification to include non-algebraic compact surfaces. The analogous classification of surfaces in positive characteristic was begun by and completed by ; it is similar to the characteristic 0 projective case, except that one also gets singular and supersingular Enriques surfaces in characteristic 2, and quasi-hyperelliptic surfaces in characteristics 2 and 3. Statement of the classification The Enriques–Kodaira classificati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |