|
Higraph
A higraph is a diagramming object that formalizes relations into a visual structure. It was developed by David Harel in 1988. Higraphs extend mathematical graphs by including notions of depth and orthogonality. In particular, nodes in a higraph can contain other nodes inside them, creating a hierarchy. The idea was initially developed for applications to databases, knowledge representation, and the behavioral specification of complex concurrent systems using the higraph-based language of statecharts. Higraphs are widely used in industrial applications like UML. Recently they have been used by philosophers to formally study the use of diagrams in mathematical proof A mathematical proof is a deductive reasoning, deductive Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use othe ...s and reasoning. References *{{citation, first=D., last=Harel , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
David Harel
David Harel (; born 12 April 1950) is a computer scientist, currently serving as President of the Israel Academy of Sciences and Humanities. He has been on the faculty of the Weizmann Institute of Science in Israel since 1980, and holds the William Sussman Professorial Chair of Mathematics. Born in London, England, he was Dean of the Faculty of Mathematics and Computer Science at the institute for seven years. Biography Harel is best known for his work on dynamic logic, computability, database theory, software engineering and modelling biological systems. In the 1980s he invented the graphical language of Statecharts for specifying and programming reactive systems, which has been adopted as part of the UML standard. Since the late 1990s he has concentrated on a scenario-based approach to programming such systems, launched by his co-invention (with W. Damm) of Live Sequence Charts. He has published expository accounts of computer science, such as his award-winning 1987 book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph (discrete Mathematics)
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a Set (mathematics), set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing mon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendicular'' is more specifically used for lines and planes that intersect to form a right angle, whereas ''orthogonal'' is used in generalizations, such as ''orthogonal vectors'' or ''orthogonal curves''. ''Orthogonality'' is also used with various meanings that are often weakly related or not related at all with the mathematical meanings. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics Optics In optics, polarization states are said to be ort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Node (graph Theory)
In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another. From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects. The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex ''w'' is said to be a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Databases
In computing, a database is an organized collection of data or a type of data store based on the use of a database management system (DBMS), the software that interacts with end users, applications, and the database itself to capture and analyze the data. The DBMS additionally encompasses the core facilities provided to administer the database. The sum total of the database, the DBMS and the associated applications can be referred to as a database system. Often the term "database" is also used loosely to refer to any of the DBMS, the database system or an application associated with the database. Before digital storage and retrieval of data have become widespread, index cards were used for data storage in a wide range of applications and environments: in the home to record and store recipes, shopping lists, contact information and other organizational data; in business to record presentation notes, project research and notes, and contact information; in schools as flash card ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Knowledge Representation
Knowledge representation (KR) aims to model information in a structured manner to formally represent it as knowledge in knowledge-based systems whereas knowledge representation and reasoning (KRR, KR&R, or KR²) also aims to understand, reason, and interpret knowledge. KRR is widely used in the field of artificial intelligence (AI) with the goal to represent information about the world in a form that a computer system can use to solve complex tasks, such as diagnosing a medical condition or having a natural-language dialog. KR incorporates findings from psychology about how humans solve problems and represent knowledge, in order to design formalisms that make complex systems easier to design and build. KRR also incorporates findings from logic to automate various kinds of ''reasoning''. Traditional KRR focuses more on the declarative representation of knowledge. Related knowledge representation formalisms mainly include vocabularies, thesaurus, semantic networks, axiom system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Concurrent Systems
Concurrency refers to the ability of a system to execute multiple tasks through simultaneous execution or time-sharing (context switching), sharing resources and managing interactions. Concurrency improves responsiveness, throughput, and scalability in modern computing, including: * Operating systems and embedded systems * Distributed systems, parallel computing, and high-performance computing * Database systems, web applications, and cloud computing Related concepts Concurrency is a broader concept that encompasses several related ideas, including: * Parallelism (simultaneous execution on multiple processing units). Parallelism executes tasks independently on multiple CPU cores. Concurrency allows for multiple ''threads of control'' at the program level, which can use parallelism or time-slicing to perform these tasks. Programs may exhibit parallelism only, concurrency only, both parallelism and concurrency, neither. * Multi-threading and multi-processing (shared system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
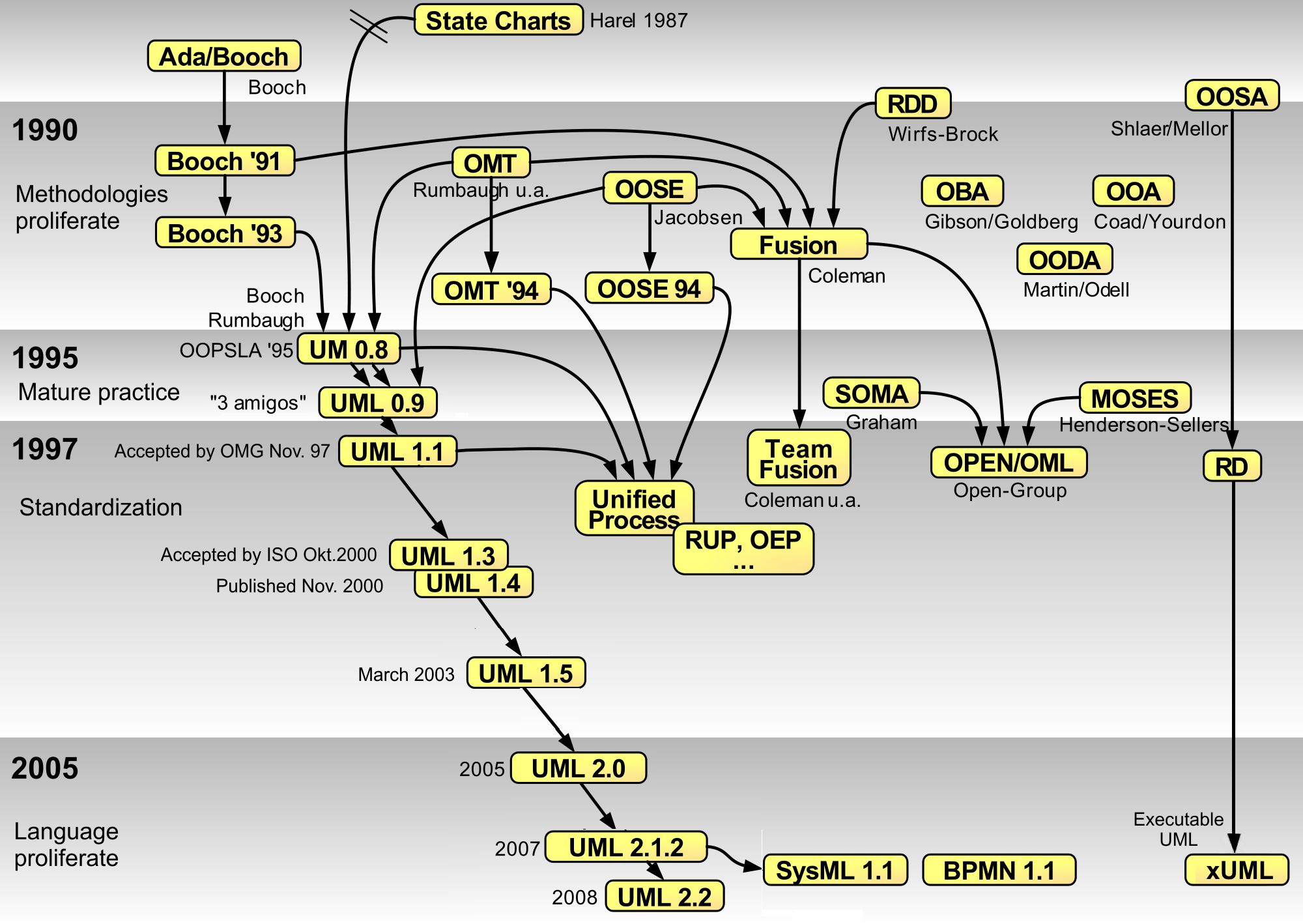
Unified Modeling Language
The Unified Modeling Language (UML) is a general-purpose visual modeling language that is intended to provide a standard way to visualize the design of a system. UML provides a standard notation for many types of diagrams which can be roughly divided into three main groups: behavior diagrams, interaction diagrams, and structure diagrams. The creation of UML was originally motivated by the desire to standardize the disparate notational systems and approaches to software design. It was developed at Rational Software in 1994–1995, with further development led by them through 1996. In 1997, UML was adopted as a standard by the Object Management Group (OMG) and has been managed by this organization ever since. In 2005, UML was also published by the International Organization for Standardization (ISO) and the International Electrotechnical Commission (IEC) as the ISO/IEC 19501 standard. Since then the standard has been periodically revised to cover the latest revision of UML. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Philosophers
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, value, mind, and language. It is a rational and critical inquiry that reflects on its methods and assumptions. Historically, many of the individual sciences, such as physics and psychology, formed part of philosophy. However, they are considered separate academic disciplines in the modern sense of the term. Influential traditions in the history of philosophy include Western, Arabic–Persian, Indian, and Chinese philosophy. Western philosophy originated in Ancient Greece and covers a wide area of philosophical subfields. A central topic in Arabic–Persian philosophy is the relation between reason and revelation. Indian philosophy combines the spiritual problem of how to reach enlightenment with the exploration of the nature of reality and the ways of arriving at knowledge. Chinese philosophy focuses principally o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diagrams
A diagram is a symbolic representation of information using visualization techniques. Diagrams have been used since prehistoric times on walls of caves, but became more prevalent during the Enlightenment. Sometimes, the technique uses a three-dimensional visualization which is then projected onto a two-dimensional surface. The word '' graph'' is sometimes used as a synonym for diagram. Overview The term "diagram" in its commonly used sense can have a general or specific meaning: * ''visual information device'' : Like the term "illustration", "diagram" is used as a collective term standing for the whole class of technical genres, including graphs, technical drawings and tables. * ''specific kind of visual display'' : This is the genre that shows qualitative data with shapes that are connected by lines, arrows, or other visual links. In science the term is used in both ways. For example, Anderson (1997) stated more generally: "diagrams are pictorial, yet abstract, represen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Proof
A mathematical proof is a deductive reasoning, deductive Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning that establish logical certainty, to be distinguished from empirical evidence, empirical arguments or non-exhaustive inductive reasoning that establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |