|
Hooke's Law Of Elasticity
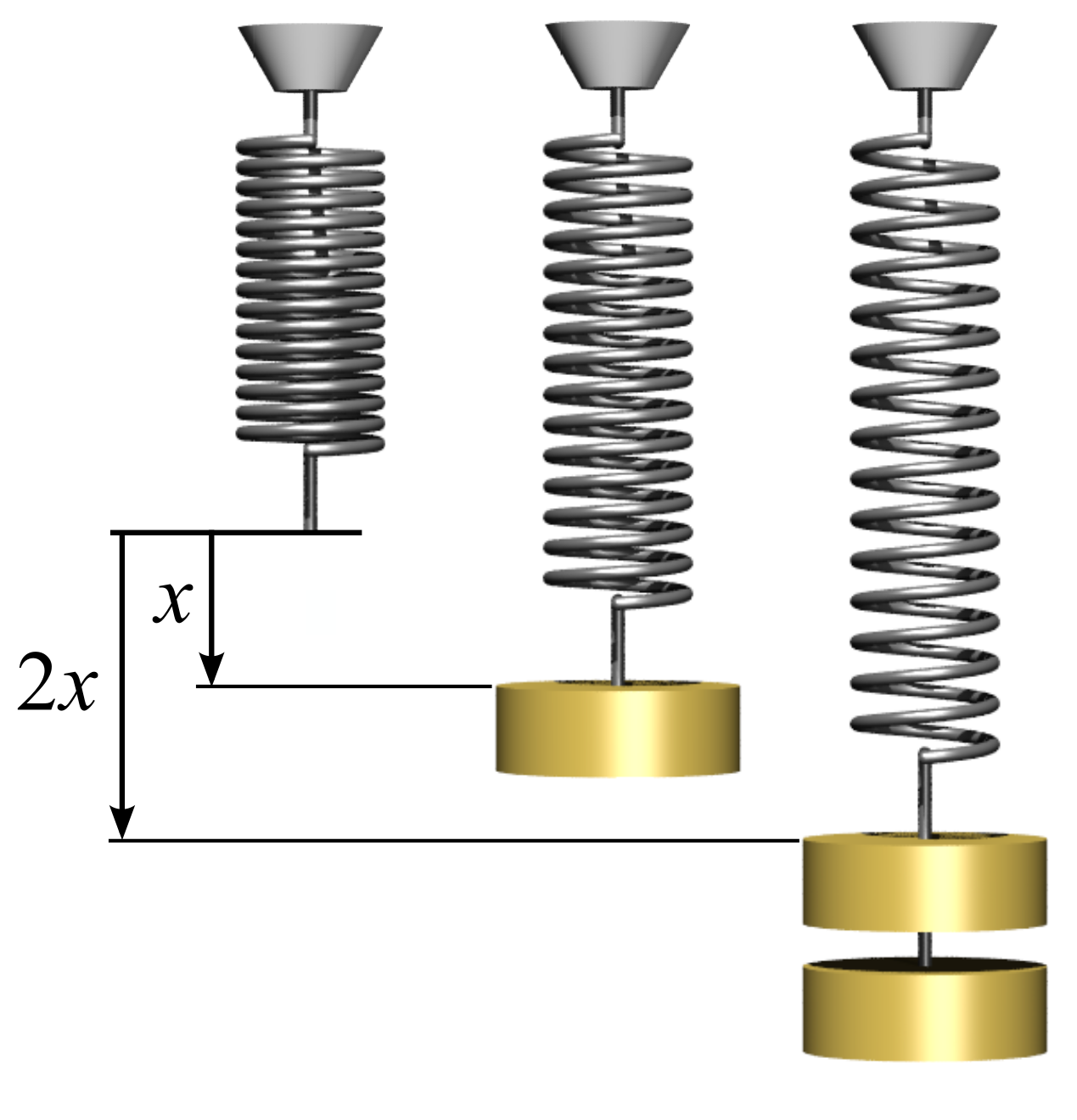
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Limit
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation. The yield strength or yield stress is a material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable load in a mechanical component, since it represents the upper limit to forces that can be applied without producing permanent deformation. In some materials, such as aluminium, there is a gradual onset of non-linear behavior, making the precise yield point difficult to determine. In such a case, the offset yiel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics (stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), general relativity ( stress–energy tensor, cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a Map (mathematics), mapping V \to W between two vector spaces that preserves the operations of vector addition and scalar multiplication. The same names and the same definition are also used for the more general case of module (mathematics), modules over a ring (mathematics), ring; see Module homomorphism. If a linear map is a bijection then it is called a . In the case where V = W, a linear map is called a (linear) ''endomorphism''. Sometimes the term refers to this case, but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that V and W are Real number, real vector spaces (not necessarily with V = W), or it can be used to emphasize that V is a function space, which is a common convention in functional analysis. Some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (mechanics)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body. A deformation can occur because of external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. Strain is related to deformation in terms of ''relative'' displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. The rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Elasticity
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents. Solid mechanics is fundamental for civil, aerospace, nuclear, biomedical and mechanical engineering, for geology, and for many branches of physics such as materials science. It has specific applications in many other areas, such as understanding the anatomy of living beings, and the design of dental prostheses and surgical implants. One of the most common practical applications of solid mechanics is the Euler–Bernoulli beam equation. Solid mechanics extensively uses tensors to describe stresses, strains, and the relationship between them. Solid mechanics is a vast subject because of the wide range of solid materials available, such as steel, wood, concrete, biological materials, textiles, geological ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Clock
A clock or a timepiece is a device used to measure and indicate time. The clock is one of the oldest human inventions, meeting the need to measure intervals of time shorter than the natural units such as the day, the lunar month and the year. Devices operating on several physical processes have been used over the millennia. Some predecessors to the modern clock may be considered as "clocks" that are based on movement in nature: A sundial shows the time by displaying the position of a shadow on a flat surface. There is a range of duration timers, a well-known example being the hourglass. Water clocks, along with the sundials, are possibly the oldest time-measuring instruments. A major advance occurred with the invention of the verge escapement, which made possible the first mechanical clocks around 1300 in Europe, which kept time with oscillating timekeepers like balance wheels., pp. 103–104., p. 31. Traditionally, in horology, the term ''clock'' was used for a stri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Balance Wheel
A balance wheel, or balance, is the timekeeping device used in mechanical watches and small clocks, analogous to the pendulum in a pendulum clock. It is a weighted wheel that rotates back and forth, being returned toward its center position by a spiral torsion spring, known as the balance spring or ''hairspring''. It is driven by the escapement, which transforms the rotating motion of the watch gear train into impulses delivered to the balance wheel. Each swing of the wheel (called a "tick" or "beat") allows the gear train to advance a set amount, moving the hands forward. The balance wheel and hairspring together form a harmonic oscillator, which due to resonance oscillates preferentially at a certain rate, its resonant frequency or "beat", and resists oscillating at other rates. The combination of the mass of the balance wheel and the elasticity of the spring keep the time between each oscillation or "tick" very constant, accounting for its nearly universal use as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galvanometer
A galvanometer is an electromechanical measuring instrument for electric current. Early galvanometers were uncalibrated, but improved versions, called ammeters, were calibrated and could measure the flow of current more precisely. A galvanometer works by deflecting a pointer in response to an electric current flowing through a coil in a constant magnetic field. Galvanometers can be thought of as a kind of actuator. Galvanometers came from the observation, first noted by Hans Christian Ørsted in 1820, that a magnetic compass's needle deflects when near a wire having electric current. They were the first instruments used to detect and measure small amounts of current. André-Marie Ampère, who gave mathematical expression to Ørsted's discovery, named the instrument after the Italian electricity researcher Luigi Galvani, who in 1791 discovered the principle of the frog galvanoscope – that electric current would make the legs of a dead frog jerk. Galvanometers have bee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manometer
Pressure measurement is the measurement of an applied force by a fluid (liquid or gas) on a surface. Pressure is typically measured in units of force per unit of surface area. Many techniques have been developed for the measurement of pressure and vacuum. Instruments used to measure and display pressure mechanically are called pressure gauges, vacuum gauges or compound gauges (vacuum & pressure). The widely used Bourdon gauge is a mechanical device, which both measures and indicates and is probably the best known type of gauge. A vacuum gauge is used to measure pressures lower than the ambient atmospheric pressure, which is set as the zero point, in negative values (for instance, −1 bar or −760 mmHg equals total vacuum). Most gauges measure pressure relative to atmospheric pressure as the zero point, so this form of reading is simply referred to as "gauge pressure". However, anything greater than total vacuum is technically a form of pressure. For very low press ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spring Scale
A spring scale, spring balance or newton meter is a type of mechanical force gauge or weighing scale. It consists of a spring fixed at one end with a hook to attach an object at the other. It works in accordance with Hooke's Law, which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance. Therefore, the scale markings on the spring balance are equally spaced. A spring balance can be calibrated for the accurate measurement of mass in the location in which they are used, but many spring balances are marked right on their face "Not Legal for Trade" or words of similar import due to the approximate nature of the theory used to mark the scale. Also, the spring in the scale can permanently stretch with repeated use. A spring scale will only read correctly in a frame of reference where the acceleration in the spring axis is constant (such as on earth, where the acceleration is due to gravity). This can be shown by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)



