|
Hartley's Test
In statistics, Hartley's test, also known as the ''F''max test or Hartley's ''F''max, is used in the analysis of variance to verify that different groups have a similar variance, an assumption needed for other statistical tests. It was developed by H. O. Hartley, who published it in 1950. The test involves computing the ratio of the largest group variance, max(sj2) to the smallest group variance, min(sj2). The resulting ratio, Fmax, is then compared to a critical value from a table of the sampling distribution of Fmax. If the computed ratio is less than the critical value, the groups are assumed to have similar or equal variances. Hartley's test assumes that data for each group are normally distributed, and that each group has an equal number of members. This test, although convenient, is quite sensitive to violations of the normality assumption.O'Brien (1981) Alternatives to Hartley's test that are robust to violations of normality are O'Brien's procedure,O'Brien (1981) and the B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Herman Otto Hartley
Herman Otto Hartley (born Hermann Otto Hirschfeld in Berlin, Germany; 1912–1980) was a German American statistician. He made significant contributions in many areas of statistics, mathematical programming, and optimization. He also founded Texas A&M University's Department of Statistics. Hartley's earliest papers appeared under the name H.O. Hirschfeld. His father having been born in England, Hartley had dual nationality. He cleverly translated his German last name Hirschfeld (Hirsch = Hart, Feld = field = lea = ley) into English. Career In 1934, at the age of 22, Hartley earned a Ph.D. in mathematics from the University of Berlin, followed by a Ph.D. in mathematical statistics from the University of Cambridge in 1940 and a Doctorate of Science in mathematical statistics from University College London in 1954. He began his independent academic career at UCL, where he met Egon Pearson, with whom he collaborated to produce the classic two-volume ''Biometrika Tables for Sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3). Similarly, the ratio of lemons to oranges is 6:8 (or 3:4) and the ratio of oranges to the total amount of fruit is 8:14 (or 4:7). The numbers in a ratio may be quantities of any kind, such as counts of people or objects, or such as measurements of lengths, weights, time, etc. In most contexts, both numbers are restricted to be positive. A ratio may be specified either by giving both constituting numbers, written as "''a'' to ''b''" or "''a'':''b''", or by giving just the value of their quotient Equal quotients correspond to equal ratios. Consequently, a ratio may be considered as an ordered pair of numbers, a fraction with the first number in the numerator and the second in the denominator, or as the value denoted by this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling Distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given random-sample-based statistic. If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value of a statistic (such as, for example, the sample mean or sample variance) for each sample, then the sampling distribution is the probability distribution of the values that the statistic takes on. In many contexts, only one sample is observed, but the sampling distribution can be found theoretically. Sampling distributions are important in statistics because they provide a major simplification en route to statistical inference. More specifically, they allow analytical considerations to be based on the probability distribution of a statistic, rather than on the joint probability distribution of all the individual sample values. Introduction The sampling distribution of a statistic is the distrib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brown–Forsythe Test
The Brown–Forsythe test is a statistical test for the equality of group variances based on performing an Analysis of Variance (ANOVA) on a transformation of the response variable. When a one-way ANOVA is performed, samples are assumed to have been drawn from distributions with equal variance. If this assumption is not valid, the resulting ''F''-test is invalid. The Brown–Forsythe test statistic is the F statistic resulting from an ordinary one-way analysis of variance on the absolute deviations of the groups or treatments data from their individual medians. Transformation The transformed response variable is constructed to measure the spread in each group. Let : z_=\left\vert y_ - \tilde_j \right\vert where \tilde_j is the median of group ''j''. The Brown–Forsythe test statistic is the model ''F'' statistic from a one way ANOVA on ''zij'': : F = \frac \frac where ''p'' is the number of groups, ''nj'' is the number of observations in group ''j'', and ''N'' is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cochran's C Test
In statistics, Cochran's C test, named after William G. Cochran, is a one-sided upper limit variance outlier test. The C test is used to decide if a single estimate of a variance (or a standard deviation) is significantly larger than a group of variances (or standard deviations) with which the single estimate is supposed to be comparable. The C test is discussed in many text books P. Konieczka, J. Namieśnik, Quality Assurance and Quality Control in the Analytical Chemical Laboratory – A Practical Approach, CRC Press, Boca Raton, Florida, 2009; . and has been recommended by IUPAC W. Horwitz, Harmonized protocol for the design and interpretation of collaborative studies, Trends in Analytical Chemistry 7(4), 118–120 (April 1988). and ISO.ISO Standard 5725–2:1994, “Accuracy (trueness and precision) of measurement methods and results – Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method”, International Organiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bartlett's Test
In statistics, Bartlett's test, named after Maurice Stevenson Bartlett, is used to test homoscedasticity, that is, if multiple samples are from populations with equal variances. Some statistical tests, such as the analysis of variance, assume that variances are equal across groups or samples, which can be verified with Bartlett's test. In a Bartlett test, we construct the null and alternative hypothesis. For this purpose several test procedures have been devised. The test procedure due to M.S.E (Mean Square Error/Estimator) Bartlett test is represented here. This test procedure is based on the statistic whose sampling distribution is approximately a Chi-Square distribution with (''k'' − 1) degrees of freedom, where ''k'' is the number of random samples, which may vary in size and are each drawn from independent normal distributions. Bartlett's test is sensitive to departures from normality. That is, if the samples come from non-normal distributions, then Bartlett's test may sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
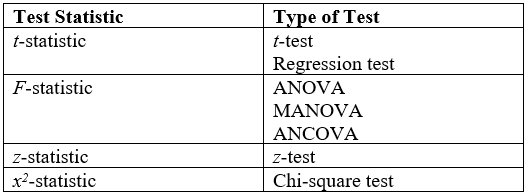
Statistical Tests
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset ( Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |