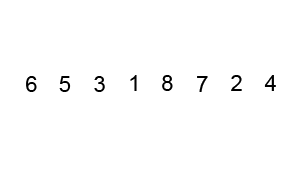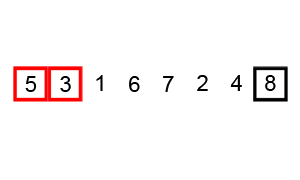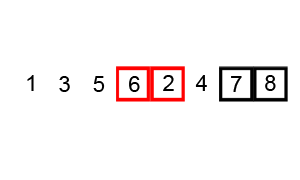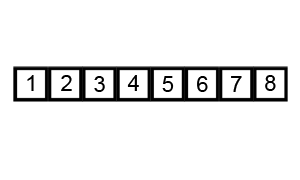|
Guarded Commands
The Guarded Command Language (GCL) is a programming language defined by Edsger Dijkstra for predicate transformer semantics in EWD472. It combines programming concepts in a compact way. It makes it easier to develop a program and its proof hand-in-hand, with the proof ideas leading the way; moreover, parts of a program can actually be ''calculated''. An important property of GCL is nondeterminism. For example, in the if-statement, several alternatives may be true, and the choice is made at runtime, when the if-statement is executed. This frees the programmer from having to make unnecessary choices and is an aid in the formal development of programs. GCL includes the multiple assignment statement. For example, execution of the statement is done by first evaluating the righthand side values and then storing them in the lefthand variables. Thus, this statement swaps the values of and . The following books discuss the development of programs using GCL: * * * * * Guarded command ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Programming Language
A programming language is a system of notation for writing computer programs. Programming languages are described in terms of their Syntax (programming languages), syntax (form) and semantics (computer science), semantics (meaning), usually defined by a formal language. Languages usually provide features such as a type system, Variable (computer science), variables, and mechanisms for Exception handling (programming), error handling. An Programming language implementation, implementation of a programming language is required in order to Execution (computing), execute programs, namely an Interpreter (computing), interpreter or a compiler. An interpreter directly executes the source code, while a compiler produces an executable program. Computer architecture has strongly influenced the design of programming languages, with the most common type (imperative languages—which implement operations in a specified order) developed to perform well on the popular von Neumann architecture. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Side Effect (computer Science)
In computer science, an operation, function or expression is said to have a side effect if it has any observable effect other than its primary effect of reading the value of its arguments and returning a value to the invoker of the operation. Example side effects include modifying a non-local variable, a static local variable or a mutable argument passed by reference; raising errors or exceptions; performing I/O; or calling other functions with side-effects. In the presence of side effects, a program's behaviour may depend on history; that is, the order of evaluation matters. Understanding and debugging a function with side effects requires knowledge about the context and its possible histories. Side effects play an important role in the design and analysis of programming languages. The degree to which side effects are used depends on the programming paradigm. For example, imperative programming is commonly used to produce side effects, to update a system's state. By contrast ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Methods
In computer science, formal methods are mathematics, mathematically rigorous techniques for the formal specification, specification, development, Program analysis, analysis, and formal verification, verification of software and computer hardware, hardware systems. The use of formal methods for software and hardware design is motivated by the expectation that, as in other engineering disciplines, performing appropriate mathematical analysis can contribute to the reliability and robustness of a design. Formal methods employ a variety of theoretical computer science fundamentals, including logic in computer science, logic calculi, formal languages, automata theory, control theory, program semantics, type systems, and type theory. Uses Formal methods can be applied at various points through the software development process, development process. Specification Formal methods may be used to give a formal description of the system to be developed, at whatever level of detail desired. F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refinement Calculus
The refinement calculus is a formalized approach to stepwise refinement for program construction. The required behaviour of the final executable program is specified as an abstract and perhaps non-executable "program", which is then refined by a series of correctness-preserving transformations into an efficiently executable program. Proponents include Ralph-Johan Back, who originated the approach in his 1978 PhD thesis ''On the Correctness of Refinement Steps in Program Development'', and Carroll Morgan, especially with his book Programming from Specifications' (Prentice Hall, 2nd edition, 1994, ). In the latter case, the motivation was to link Abrial's specification notation Z, via a rigorous relation of behaviour-preserving program refinement Refinement is a generic term of computer science that encompasses various approaches for producing correct computer programs and simplifying existing programs to enable their formal verification. Program refinement In formal methods, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (order)
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join (mathematics), join) and a unique infimum (also called a greatest lower bound or meet (mathematics), meet). An example is given by the power set of a set, partially ordered by Subset, inclusion, for which the supremum is the Union (set theory), union and the infimum is the Intersection (set theory), intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic Identity (mathematics), identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilatti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congruence Relation
In abstract algebra, a congruence relation (or simply congruence) is an equivalence relation on an algebraic structure (such as a group (mathematics), group, ring (mathematics), ring, or vector space) that is compatible with the structure in the sense that algebraic operations done with equivalent elements will yield equivalent elements. Every congruence relation has a corresponding Equivalence class, quotient structure, whose elements are the equivalence classes (or congruence classes) for the relation. Definition The definition of a congruence depends on the type of algebraic structure under consideration. Particular definitions of congruence can be made for group (mathematics), groups, ring (mathematics), rings, vector spaces, module (mathematics), modules, semigroups, lattice (order), lattices, and so forth. The common theme is that a congruence is an equivalence relation on an algebraic object that is compatible with the algebraic structure, in the sense that the operat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arg Max
In mathematics, the arguments of the maxima (abbreviated arg max or argmax) and arguments of the minima (abbreviated arg min or argmin) are the input points at which a Function (mathematics), function output value is Maxima and minima, maximized and minimized, respectively.For clarity, we refer to the input (''x'') as ''points'' and the output (''y'') as ''values;'' compare critical point (mathematics), critical point and critical value (critical point), critical value. While the argument of a function, arguments are defined over the domain of a function, the output is part of its codomain. Definition Given an arbitrary set (mathematics), set a totally ordered set and a function, the \operatorname over some subset S of X is defined by :\operatorname_S f := \underset\, f(x) := \. If S = X or S is clear from the context, then S is often left out, as in \underset\, f(x) := \. In other words, \operatorname is the Set (mathematics), set of points x for which f(x) attains the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bubble Sort
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the input list element by element, comparing the current element with the one after it, Swap (computer science), swapping their values if needed. These passes through the list are repeated until no swaps have to be performed during a pass, meaning that the list has become fully sorted. The algorithm, which is a comparison sort, is named for the way the larger elements "bubble" up to the top of the list. It performs poorly in real-world use and is used primarily as an educational tool. More efficient algorithms such as quicksort, timsort, or merge sort are used by the sorting libraries built into popular programming languages such as Python and Java. History The earliest description of the bubble sort algorithm was in a 1956 paper by mathematician and actuary Edward Harry Friend, ''Sorting on electronic computer systems'', published in the third issue of the third volume ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bézout's Identity
In mathematics, Bézout's identity (also called Bézout's lemma), named after Étienne Bézout who proved it for polynomials, is the following theorem: Here the greatest common divisor of and is taken to be . The integers and are called Bézout coefficients for ; they are not unique. A pair of Bézout coefficients can be computed by the extended Euclidean algorithm, and this pair is, in the case of integers one of the two pairs such that and ; equality occurs only if one of and is a multiple of the other. As an example, the greatest common divisor of 15 and 69 is 3, and 3 can be written as a combination of 15 and 69 as , with Bézout coefficients −9 and 2. Many other theorems in elementary number theory, such as Euclid's lemma or the Chinese remainder theorem, result from Bézout's identity. A Bézout domain is an integral domain in which Bézout's identity holds. In particular, Bézout's identity holds in principal ideal domains. Every theorem that results from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extended Euclidean Algorithm
In arithmetic and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common divisor (gcd) of integers ''a'' and ''b'', also the coefficients of Bézout's identity, which are integers ''x'' and ''y'' such that : ax + by = \gcd(a, b). This is a certifying algorithm, because the gcd is the only number that can simultaneously satisfy this equation and divide the inputs. It allows one to compute also, with almost no extra cost, the quotients of ''a'' and ''b'' by their greatest common divisor. also refers to a very similar algorithm for computing the polynomial greatest common divisor and the coefficients of Bézout's identity of two univariate polynomials. The extended Euclidean algorithm is particularly useful when ''a'' and ''b'' are coprime. With that provision, ''x'' is the modular multiplicative inverse of ''a'' modulo ''b'', and ''y'' is the modular multiplicative inverse of ''b'' mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greatest Common Divisor
In mathematics, the greatest common divisor (GCD), also known as greatest common factor (GCF), of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers , , the greatest common divisor of and is denoted \gcd (x,y). For example, the GCD of 8 and 12 is 4, that is, . In the name "greatest common divisor", the adjective "greatest" may be replaced by "highest", and the word "divisor" may be replaced by "factor", so that other names include highest common factor, etc. Historically, other names for the same concept have included greatest common measure. This notion can be extended to polynomials (see ''Polynomial greatest common divisor'') and other commutative rings (see ' below). Overview Definition The ''greatest common divisor'' (GCD) of integers and , at least one of which is nonzero, is the greatest positive integer such that is a divisor of both and ; that is, there are integers and such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Algorithm
In mathematics, the Euclidean algorithm,Some widely used textbooks, such as I. N. Herstein's ''Topics in Algebra'' and Serge Lang's ''Algebra'', use the term "Euclidean algorithm" to refer to Euclidean division or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his ''Elements'' (). It is an example of an ''algorithm'', a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |