|
Green's Function (many-body Theory)
In many-body theory, the term Green's function (or Green function) is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators. The name comes from the Green's functions used to solve inhomogeneous differential equations, to which they are loosely related. (Specifically, only two-point "Green's functions" in the case of a non-interacting system are Green's functions in the mathematical sense; the linear operator that they invert is the Hamiltonian operator, which in the non-interacting case is quadratic in the fields.) Spatially uniform case Basic definitions We consider a many-body theory with field operator (annihilation operator written in the position basis) \psi(\mathbf). The Heisenberg operators can be written in terms of Schrödinger operators as \psi(\mathbf,t) = e^ \psi(\mathbf) e^, and the creation operator is \bar\psi(\mathbf,t) = psi(\mathbf,t)\dagger, where K = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Many-body Theory
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of many interacting particles. Terminology ''Microscopic'' here implies that quantum mechanics has to be used to provide an accurate description of the system. ''Many'' can be anywhere from three to infinity (in the case of a practically infinite, homogeneous or periodic system, such as a crystal), although three- and four-body systems can be treated by specific means (respectively the Faddeev and Faddeev–Yakubovsky equations) and are thus sometimes separately classified as few-body systems. Explanation of the problem In general terms, while the underlying physical laws that govern the motion of each individual particle may (or may not) be simple, the study of the collection of particles can be extremely complex. In such a quantum system, the repeated interactions between particles create quantum correlations, or entanglement. As a consequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory. Group theory The commutator of two elements, and , of a group , is the element : . This element is equal to the group's identity if and only if and commute (that is, if and only if ). The set of all commutators of a group is not in general closed under the group operation, but the subgroup of ''G'' generated by all commutators is closed and is called the ''derived group'' or the '' commutator subgroup'' of ''G''. Commutators are used to define nilpotent and solvable groups and the largest abelian quotient group. The definition of the commutator above is used throughout this article, but many group theorists define the commutator as : . Using the first definition, this can be expressed as . Identities (group theory) Commutator identities are an important tool in group th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Numerical Analytic Continuation
In many-body physics, the problem of analytic continuation is that of numerically extracting the spectral density of a Green function given its values on the imaginary axis. It is a necessary post-processing step for calculating dynamical properties of physical systems from Quantum Monte Carlo simulations, which often compute Green function values only at imaginary times or Matsubara frequencies. Mathematically, the problem reduces to solving a Fredholm integral equation of the first kind with an ill-conditioned kernel. As a result, it is an ill-posed inverse problem with no unique solution and where a small noise on the input leads to large errors in the unregularized solution. There are different methods for solving this problem including the maximum entropy method, the average spectrum method and Pade approximation methods. Examples A common analytic continuation problem is obtaining the spectral function A(\omega) at real frequencies \omega from the Green function values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Propagator
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. Propagators may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called ''(causal) Green's functions'' (called "''causal''" to distinguish it from the elliptic Laplacian Green's function). Non-relativistic propagators In non-relativistic quantum mechanics, the propagator gives the probability amplitude for a particle to travel from one spatial point (x') at one time (t') to another spatial point (x) at a later time (t). The Green's function G for the Schrödinger equat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lindblad Equation
In quantum mechanics, the Gorini–Kossakowski–Sudarshan–Lindblad (GKSL) equation (named after Vittorio Gorini, Andrzej Kossakowski, E. C. George Sudarshan, George Sudarshan and Göran Lindblad (physicist), Göran Lindblad), master equation in Lindblad form, quantum Liouvillian, or Lindbladian is one of the general forms of Markov process, Markovian Quantum master equation, master equations describing open quantum systems. It generalizes the Schrödinger equation to open quantum systems; that is, systems in contacts with their surroundings. The resulting dynamics are no longer unitary, but still satisfy the property of being completely positive trace-preserving, trace-preserving and completely positive for any initial condition. The Schrödinger equation or, actually, the von Neumann equation, is a special case of the GKSL equation, which has led to some speculation that quantum mechanics may be productively extended and expanded through further application and analysis of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Response Function
A linear response function describes the input-output relationship of a signal transducer, such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in information theory, physics and engineering there exist alternative names for specific linear response functions such as susceptibility, impulse response or impedance; see also transfer function. The concept of a Green's function or fundamental solution of an ordinary differential equation is closely related. Mathematical definition Denote the input of a system by h(t) (e.g. a force), and the response of the system by x(t) (e.g. a position). Generally, the value of x(t) will depend not only on the present value of h(t), but also on past values. Approximately x(t) is a weighted sum of the previous values of h(t'), with the weights given by the linear response function \chi(t-t'): x(t) = \int_^t dt'\, \chi(t-t') h(t') + \cdots\,. The explicit te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Green–Kubo Relations
The Green–Kubo relations ( Melville S. Green 1954, Ryogo Kubo 1957) give the exact mathematical expression for a transport coefficient \gamma in terms of the integral of the equilibrium time correlation function of the time derivative of a corresponding microscopic variable A (sometimes termed a "gross variable", as in ): \gamma = \int_0^\infty \left\langle \dot(t) \dot(0) \right\rangle \;t. One intuitive way to understand this relation is that relaxations resulting from random fluctuations in equilibrium are indistinguishable from those due to an external perturbation in linear response. Green-Kubo relations are important because they relate a macroscopic transport coefficient to the correlation function of a microscopic variable. In addition, they allow one to measure the transport coefficient without perturbing the system out of equilibrium, which has found much use in molecular dynamics simulations. Thermal and mechanical transport processes Thermodynamic systems m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fluctuation Theorem
The fluctuation theorem (FT), which originated from statistical mechanics, deals with the relative probability that the Entropy (statistical thermodynamics), entropy of a system which is currently away from thermodynamic equilibrium (i.e., maximum entropy) will increase or decrease over a given amount of time. While the second law of thermodynamics predicts that the entropy of an isolated system should tend to increase until it reaches equilibrium, it became apparent after the discovery of statistical mechanics that the second law is only a statistical one, suggesting that there should always be some nonzero probability that the entropy of an isolated system might spontaneously ''decrease''; the fluctuation theorem precisely quantifies this probability. Statement Roughly, the fluctuation theorem relates to the probability distribution of the time-averaged irreversible entropy production, denoted \overline_t. The theorem states that, in systems away from equilibrium over a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hilbert Transform
In mathematics and signal processing, the Hilbert transform is a specific singular integral that takes a function, of a real variable and produces another function of a real variable . The Hilbert transform is given by the Cauchy principal value of the convolution with the function 1/(\pi t) (see ). The Hilbert transform has a particularly simple representation in the frequency domain: It imparts a phase shift of ±90° (/2 radians) to every frequency component of a function, the sign of the shift depending on the sign of the frequency (see ). The Hilbert transform is important in signal processing, where it is a component of the Analytic signal, analytic representation of a real-valued signal . The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions. Definition The Hilbert transform of can be thought of as the convolution of with the function , known as the Cauchy ker ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cauchy Principal Part
In mathematics, the Cauchy principal value, named after Augustin-Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined. In this method, a singularity on an integral interval is avoided by limiting the integral interval to the non singular domain. Formulation Depending on the type of singularity in the integrand , the Cauchy principal value is defined according to the following rules: In some cases it is necessary to deal simultaneously with singularities both at a finite number and at infinity. This is usually done by a limit of the form \lim_\, \lim_ \,\left ,\int_^ f(x)\,\mathrmx \,~ + ~ \int_^ f(x)\,\mathrmx \,\right In those cases where the integral may be split into two independent, finite limits, \lim_ \, \left, \,\int_a^ f(x)\,\mathrmx \,\\; < \;\infty and then the function is integrable in the ordinary sense. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
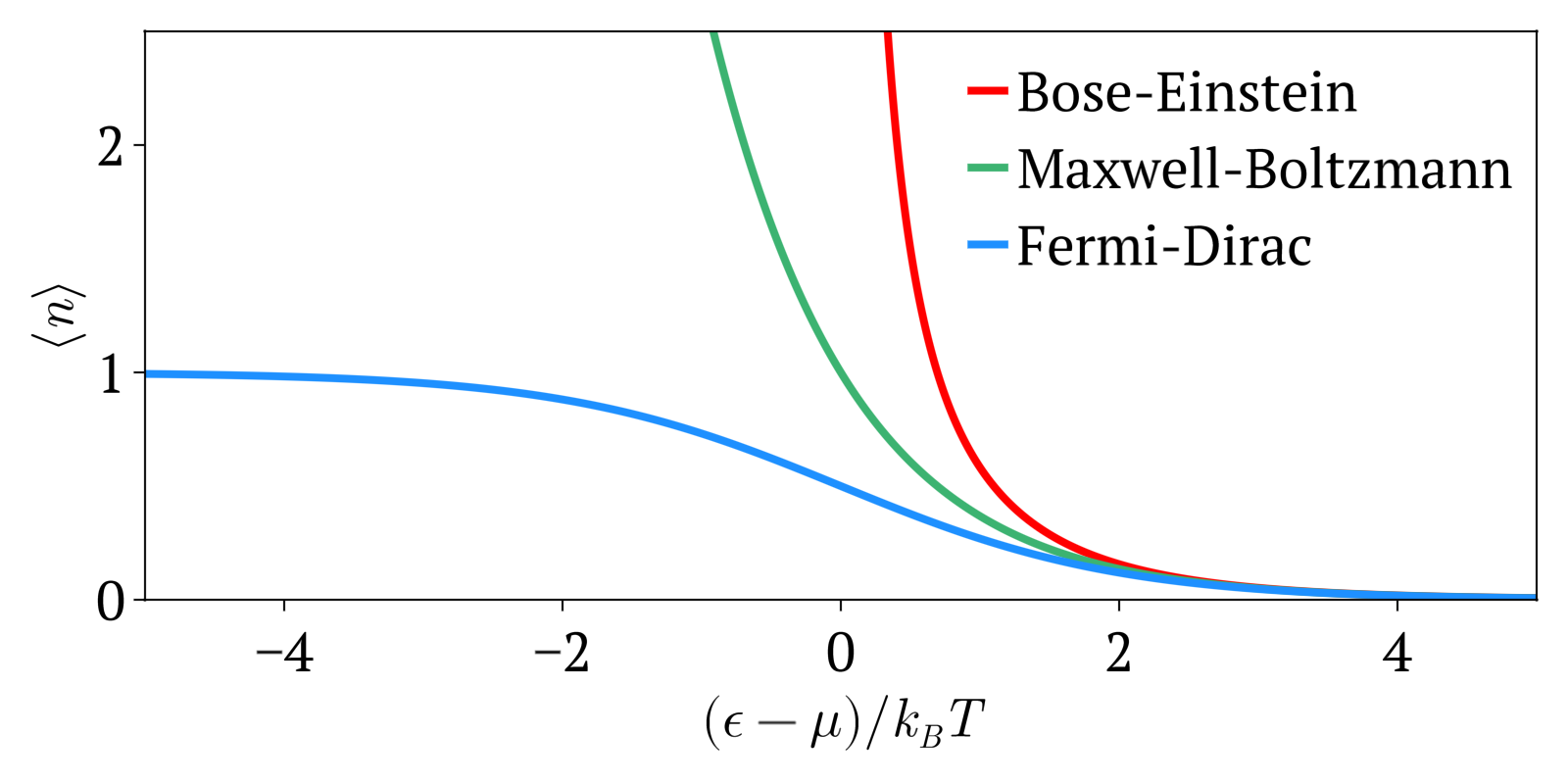
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi†... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |