|
Gauss–Newton Algorithm
The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum of squares must be nonnegative, the algorithm can be viewed as using Newton's method to iteratively approximate zeroes of the components of the sum, and thus minimizing the sum. It has the advantage that second derivatives, which can be challenging to compute, are not required. Non-linear least squares problems arise, for instance, in non-linear regression, where parameters in a model are sought such that the model is in good agreement with available observations. The method is named after the mathematicians Carl Friedrich Gauss and Isaac Newton, and first appeared in Gauss' 1809 work ''Theoria motus corporum coelestium in sectionibus conicis solem ambientum''. Description Given m functions \textbf = (r_1, \ldots, r_m) (often called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
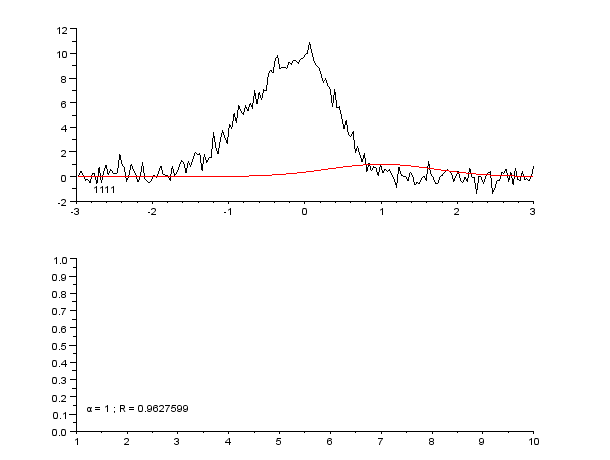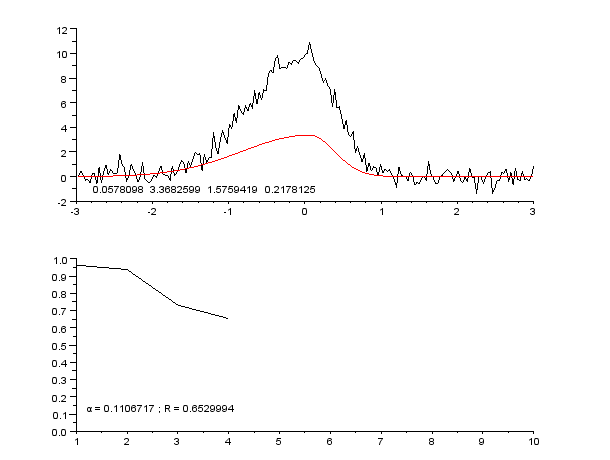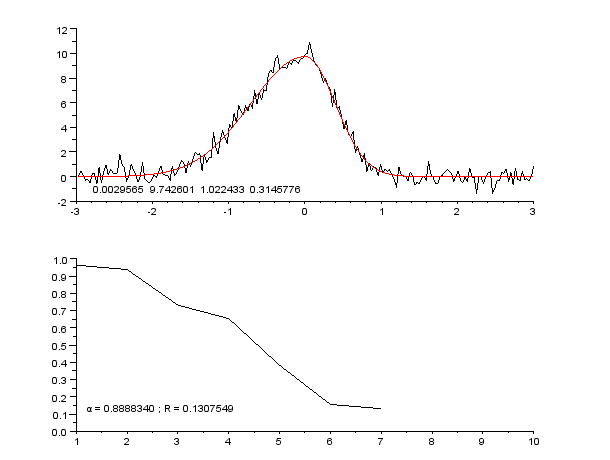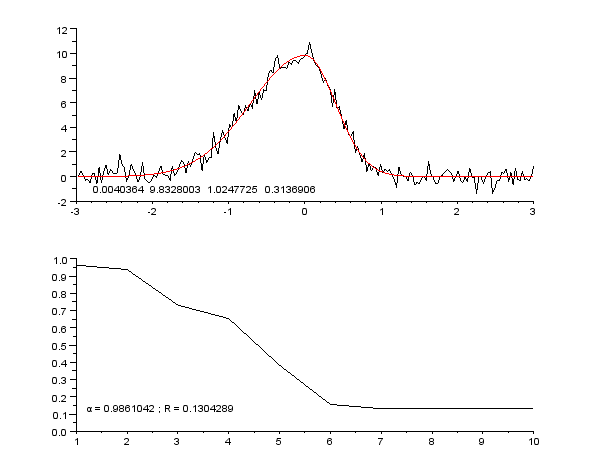
Regression Pic Assymetrique
Regression or regressions may refer to: Science * Marine regression, coastal advance due to falling sea level, the opposite of marine transgression * Regression (medicine), a characteristic of diseases to express lighter symptoms or less extent (mainly for tumors), without disappearing totally * Regression (psychology), a defensive reaction to some unaccepted impulses * Nodal regression, the movement of the nodes of an object in orbit, in the opposite direction to the motion of the object Statistics * Regression analysis, a statistical technique for estimating the relationships among variables. There are several types of regression: ** Linear regression ** Simple linear regression ** Logistic regression ** Nonlinear regression ** Nonparametric regression ** Robust regression ** Stepwise regression * Regression toward the mean, a common statistical phenomenon Computing * Software regression, the appearance of a bug which was absent in a previous revision ** Regression testing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations. Definition Given a twice continuously differentiable function f of one real variable, Taylor's theorem for the case n = 1 states that f(x) = f(a) + f'(a)(x - a) + R_2 where R_2 is the remainder term. The linear approximation is obtained by dropping the remainder: f(x) \approx f(a) + f'(a)(x - a). This is a good approximation when x is close enough to since a curve, when closely observed, will begin to resemble a straight line. Therefore, the expression on the right-hand side is just the equation for the tangent line to the graph of f at (a,f(a)). For this reason, this process is also called the tangent line approximation. If f is concave down in the interval between x and a, the approximation wil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overdetermined System
In mathematics, a system of equations is considered overdetermined if there are more equations than unknowns. An overdetermined system is almost always inconsistent (it has no solution) when constructed with random coefficients. However, an overdetermined system will have solutions in some cases, for example if some equation occurs several times in the system, or if some equations are linear combinations of the others. The terminology can be described in terms of the concept of constraint counting. Each unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom. Therefore, the critical case occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint. The ''overdetermined'' case occurs when the system has been overconstrained — that is, when the equations outnumb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ill-conditioned
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem: given f(x) = y, one is solving for ''x,'' and thus the condition number of the (local) inverse must be used. In linear regression the condition number of the moment matrix can be used as a diagnostic for multicollinearity. The condition number is an application of the derivative, and is formally defined as the value of the asymptotic worst-case relative change in output for a relative change in input. The "function" is the solution of a problem and the "arguments" are the data in the problem. The condition number is frequently applied to questions in linear algebra, in which case the derivative is straightforward but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Of Convergence
In numerical analysis, the order of convergence and the rate of convergence of a convergent sequence are quantities that represent how quickly the sequence approaches its limit. A sequence (x_n) that converges to x^* is said to have ''order of convergence'' q \geq 1 and ''rate of convergence'' \mu if : \lim _ \frac=\mu. The rate of convergence \mu is also called the ''asymptotic error constant''. Note that this terminology is not standardized and some authors will use ''rate'' where this article uses ''order'' (e.g., ). In practice, the rate and order of convergence provide useful insights when using iterative methods for calculating numerical approximations. If the order of convergence is higher, then typically fewer iterations are necessary to yield a useful approximation. Strictly speaking, however, the asymptotic behavior of a sequence does not give conclusive information about any finite part of the sequence. Similar concepts are used for discretization methods. The solutio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Method In Optimization
In calculus, Newton's method is an iterative method for finding the roots of a differentiable function , which are solutions to the equation . As such, Newton's method can be applied to the derivative of a twice-differentiable function to find the roots of the derivative (solutions to ), also known as the critical points of . These solutions may be minima, maxima, or saddle points; see section "Several variables" in Critical point (mathematics) and also section "Geometric interpretation" in this article. This is relevant in optimization, which aims to find (global) minima of the function . Newton's method The central problem of optimization is minimization of functions. Let us first consider the case of univariate functions, i.e., functions of a single real variable. We will later consider the more general and more practically useful multivariate case. Given a twice differentiable function f:\mathbb\to \mathbb, we seek to solve the optimization problem : \min_ f(x) . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Convergence
In numerical analysis, an iterative method is called locally convergent if the successive approximations produced by the method are guaranteed to converge to a solution when the initial approximation is already close enough to the solution. Iterative methods for nonlinear equation In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...s and their systems, such as Newton's method are usually only locally convergent. An iterative method that converges for an arbitrary initial approximation is called globally convergent. Iterative methods for systems of linear equations are usually globally convergent. Numerical analysis Iterative methods Optimization algorithms and methods {{mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name). For a differentiable function of several real variables, a stationary point is a point on the surface of the graph where all its partial derivatives are zero (equivalently, the gradient is zero). Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., parallel to the -axis). For a function of two variables, they correspond to the points on the graph where the tangent plane is parallel to the plane. Turning points A turning point is a point at which the derivative changes sign. A turning point may be either a relative maximum or a relative minimum (also known as local minimum and maximum). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descent Direction
In optimization, a descent direction is a vector \mathbf\in\mathbb R^n that, in the sense below, moves us closer towards a local minimum \mathbf^* of our objective function f:\mathbb R^n\to\mathbb R. Suppose we are computing \mathbf^* by an iterative method, such as line search. We define a descent direction \mathbf_k\in\mathbb R^n at the kth iterate to be any \mathbf_k such that \langle\mathbf_k,\nabla f(\mathbf_k)\rangle < 0, where denotes the . The motivation for such an approach is that small steps along guarantee that is reduced, by . Using this definition, the negative of a non-zero gradient is always a descent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss Newton Illustration
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). Ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addressed by conju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
QR Factorization
In linear algebra, a QR decomposition, also known as a QR factorization or QU factorization, is a decomposition of a matrix ''A'' into a product ''A'' = ''QR'' of an orthogonal matrix ''Q'' and an upper triangular matrix ''R''. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm. Cases and definitions Square matrix Any real square matrix ''A'' may be decomposed as : A = QR, where ''Q'' is an orthogonal matrix (its columns are orthogonal unit vectors meaning and ''R'' is an upper triangular matrix (also called right triangular matrix). If ''A'' is invertible, then the factorization is unique if we require the diagonal elements of ''R'' to be positive. If instead ''A'' is a complex square matrix, then there is a decomposition ''A'' = ''QR'' where ''Q'' is a unitary matrix (so If ''A'' has ''n'' linearly independent columns, then the first ''n'' columns of ''Q'' form an o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
