|
Gaussian Integral
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function f(x) = e^ over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is \int_^\infty e^\,dx = \sqrt. Abraham de Moivre originally discovered this type of integral in 1733, while Gauss published the precise integral in 1809, attributing its discovery to Laplace. The integral has a wide range of applications. For example, with a slight change of variables it is used to compute the normalizing constant of the normal distribution. The same integral with finite limits is closely related to both the error function and the cumulative distribution function of the normal distribution. In physics this type of integral appears frequently, for example, in quantum mechanics, to find the probability density of the ground state of the harmonic oscillator. This integral is also used in the path integral formulation, to find the propagator of the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gaussian Quadrature
In numerical analysis, an -point Gaussian quadrature rule, named after Carl Friedrich Gauss, is a quadrature rule constructed to yield an exact result for polynomials of degree or less by a suitable choice of the nodes and weights for . The modern formulation using orthogonal polynomials was developed by Carl Gustav Jacobi in 1826. The most common domain of integration for such a rule is taken as , so the rule is stated as \int_^1 f(x)\,dx \approx \sum_^n w_i f(x_i), which is exact for polynomials of degree or less. This exact rule is known as the Gauss–Legendre quadrature rule. The quadrature rule will only be an accurate approximation to the integral above if is well-approximated by a polynomial of degree or less on . The Gauss–Adrien-Marie Legendre, Legendre quadrature rule is not typically used for integrable functions with endpoint singularity (math), singularities. Instead, if the integrand can be written as f(x) = \left(1 - x\right)^\alpha \left(1 + x\right) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Indefinite Integral
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, velocity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cartesian Plane
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fubini's Theorem
In mathematical analysis, Fubini's theorem characterizes the conditions under which it is possible to compute a double integral by using an iterated integral. It was introduced by Guido Fubini in 1907. The theorem states that if a function is Lebesgue integrable on a rectangle X\times Y, then one can evaluate the double integral as an iterated integral:\, \iint\limits_ f(x,y)\,\text(x,y) = \int_X\left(\int_Y f(x,y)\,\texty\right)\textx=\int_Y\left(\int_X f(x,y) \, \textx \right) \texty. This formula is generally not true for the Riemann integral, but it is true if the function is continuous on the rectangle. In multivariable calculus, this weaker result is sometimes also called Fubini's theorem, although it was already known by Leonhard Euler. Tonelli's theorem, introduced by Leonida Tonelli in 1909, is similar but is applied to a non-negative measurable function rather than to an integrable function over its domain. The Fubini and Tonelli theorems are usually combined and for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cauchy Principal Value
In mathematics, the Cauchy principal value, named after Augustin-Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined. In this method, a singularity on an integral interval is avoided by limiting the integral interval to the non singular domain. Formulation Depending on the type of singularity in the integrand , the Cauchy principal value is defined according to the following rules: In some cases it is necessary to deal simultaneously with singularities both at a finite number and at infinity. This is usually done by a limit of the form \lim_\, \lim_ \,\left ,\int_^ f(x)\,\mathrmx \,~ + ~ \int_^ f(x)\,\mathrmx \,\right In those cases where the integral may be split into two independent, finite limits, \lim_ \, \left, \,\int_a^ f(x)\,\mathrmx \,\\; < \;\infty and then the function is integrable in the ordinary sense. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Absolutely Convergent
In mathematics, an infinite series of numbers is said to converge absolutely (or to be absolutely convergent) if the sum of the absolute values of the summands is finite. More precisely, a real or complex series \textstyle\sum_^\infty a_n is said to converge absolutely if \textstyle\sum_^\infty \left, a_n\ = L for some real number \textstyle L. Similarly, an improper integral of a function, \textstyle\int_0^\infty f(x)\,dx, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if \textstyle\int_0^\infty , f(x), dx = L. A convergent series that is not absolutely convergent is called conditionally convergent. Absolute convergence is important for the study of infinite series, because its definition guarantees that a series will have some "nice" behaviors of finite sums that not all convergent series possess. For instance, rearrangements do not change the value of the sum, which is not necessarily true for conditionally convergen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
List Of Canonical Coordinate Transformations
A list is a set of discrete items of information collected and set forth in some format for utility, entertainment, or other purposes. A list may be memorialized in any number of ways, including existing only in the mind of the list-maker, but lists are frequently written down on paper, or maintained electronically. Lists are "most frequently a tool", and "one does not ''read'' but only ''uses'' a list: one looks up the relevant information in it, but usually does not need to deal with it as a whole".Lucie Doležalová,The Potential and Limitations of Studying Lists, in Lucie Doležalová, ed., ''The Charm of a List: From the Sumerians to Computerised Data Processing'' (2009). Purpose It has been observed that, with a few exceptions, "the scholarship on lists remains fragmented". David Wallechinsky, a co-author of '' The Book of Lists'', described the attraction of lists as being "because we live in an era of overstimulation, especially in terms of information, and lists help us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jacobian Determinant
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of components of function values, then its determinant is called the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian. They are named after Carl Gustav Jacob Jacobi. The Jacobian matrix is the natural generalization to vector valued functions of several variables of the derivative and the differential of a usual function. This generalization includes generalizations of the inverse function theorem and the implicit function theorem, where the non-nullity of the derivative is replaced by the non-nullity of the Jacobian determinant, and the multiplicative inverse of the derivative is replaced by the inverse of the Jacobian matrix. The Jacobian determinant is fundamentally used for c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
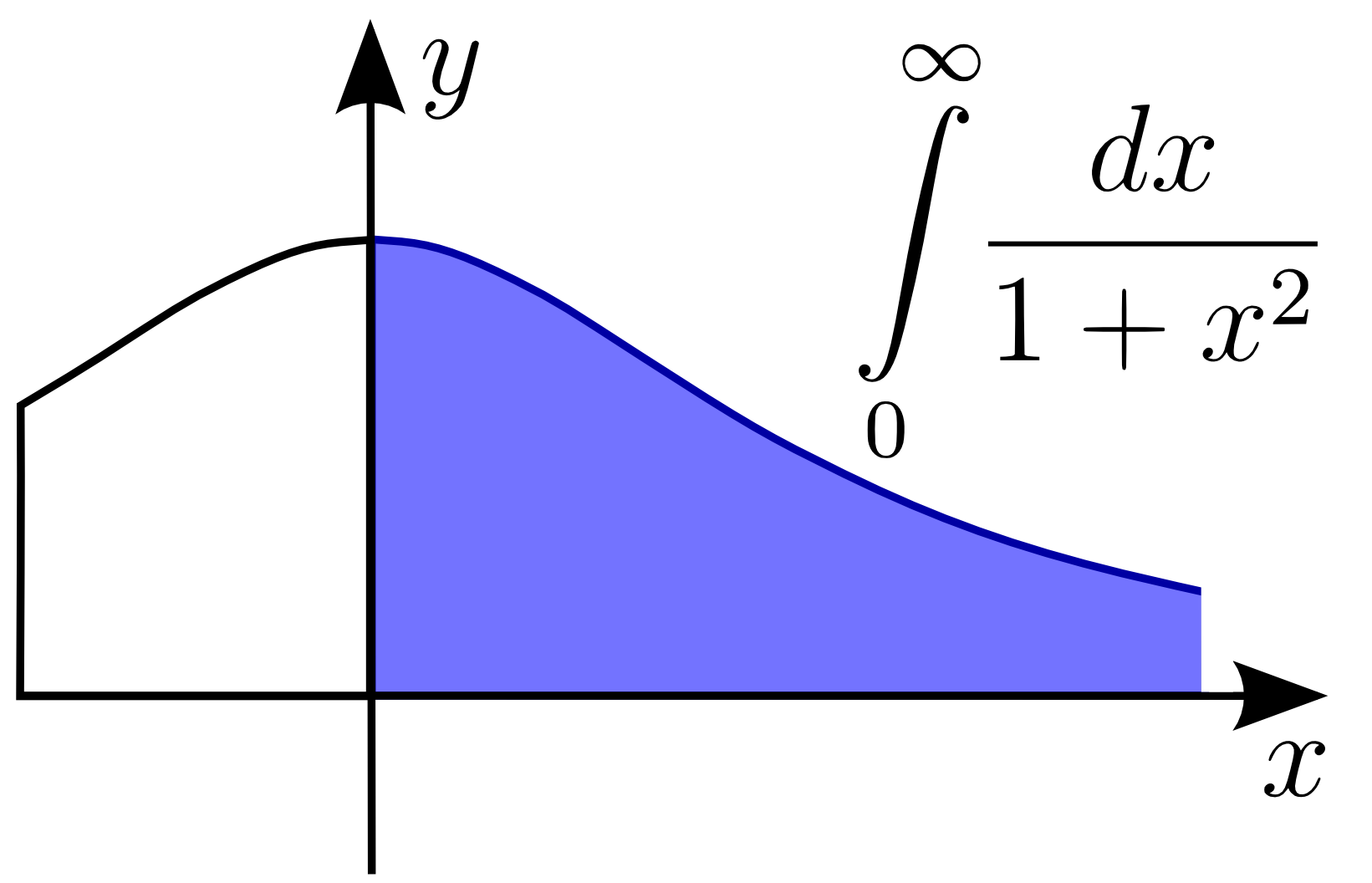
Improper Integral
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result. In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polar Coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray (geometry), ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Shell Integration
Shell integration (the shell method in integral calculus) is a method for calculating the volume of a solid of revolution, when integrating along an axis ''perpendicular to'' the axis of revolution. This is in contrast to disc integration which integrates along the axis ''parallel'' to the axis of revolution. Definition The shell method goes as follows: Consider a volume in three dimensions obtained by rotating a cross-section in the -plane around the -axis. Suppose the cross-section is defined by the graph of the positive function on the interval . Then the formula for the volume will be: :2 \pi \int_a^b x f(x)\, dx If the function is of the coordinate and the axis of rotation is the -axis then the formula becomes: :2 \pi \int_a^b y f(y)\, dy If the function is rotating around the line then the formula becomes: :\begin \displaystyle 2 \pi \int_a^b (x-h) f(x)\,dx, & \text\ h \le a < b\\ \displaystyle 2 \pi \int_a^b (h-x) f(x)\,dx, & \text\ a < b \le h, \end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |