|
Gaussian Correlation Conjecture
The Gaussian correlation inequality (GCI), formerly known as the Gaussian correlation conjecture (GCC), is a mathematical theorem in the fields of mathematical statistics and convex geometry. The statement The Gaussian correlation inequality states: Let \mu be an ''n''-dimensional Gaussian probability measure on \mathbb^n , i.e. \mu a multivariate normal distribution, centered at the origin. Then for all convex sets E,F \subset \mathbb^n that are symmetric about the origin, : \mu(E \cap F) \geq \mu(E) \cdot \mu(F). As a simple example for ''n''=2, one can think of darts being thrown at a board, with their landing spots in the plane distributed according to a 2-variable normal distribution centered at the origin. (This is a reasonable assumption for any given darts player, with different players being described by different normal distributions.) If we now consider a circle and a rectangle in the plane, both centered at the origin, then the proportion of the darts landing i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Distribution Darts Demonstration
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below. There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymous adjective ''Gaussian'' is pronounced . Mathematics Algebra and linear algebra Geometry and differential geometry Number theory Cyclotomic fields *Gaussian period *Gaussian rational *Gauss sum, an exponential sum over Dirichlet characters ** Elliptic Gauss sum, an analog of a Gauss sum **Quadratic Gauss sum Analysis, numerical analysis, vector calculus and calculus of variations Complex analysis and convex analysis *Gauss–Lucas theorem *Gauss's continued fraction, an analytic continued fraction derived from the hypergeometric functions * Gauss's criterion – described oEncyclopedia of Mathematics* Gauss's hypergeometric theorem, an identity on hypergeometric series * Gauss plane Statistics *Gauss–K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Theorem
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems. In the mainstream of mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice, or of a less powerful theory, such as Peano arithmetic. A notable exception is Wiles's proof of Fermat's Last Theorem, which involves the Grothendieck universes whose existence requires the addition of a new axiom to the set theory. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' and '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Statistics
Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory. Introduction Statistical data collection is concerned with the planning of studies, especially with the design of randomized experiments and with the planning of surveys using random sampling. The initial analysis of the data often follows the study protocol specified prior to the study being conducted. The data from a study can also be analyzed to consider secondary hypotheses inspired by the initial results, or to suggest new studies. A secondary analysis of the data from a planned study uses tools from data analysis, and the process of doing this is mathematical statistics. Data analysis is divided into: * descriptive statistics - the part of st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Geometry
In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc. Classification According to the Mathematics Subject Classification MSC2010, the mathematical discipline ''Convex and Discrete Geometry'' includes three major branches: * general convexity * polytopes and polyhedra * discrete geometry (though only portions of the latter two are included in convex geometry). General convexity is further subdivided as follows: *axiomatic and generalized convexity *convex sets without dimension restrictions *convex sets in topological vector spaces *convex sets in 2 dimensions (including convex curves) *convex sets in 3 dimensions (including convex surfaces) *convex sets in ''n'' dimensions (including convex hy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Set
In mathematics, a nonempty subset of a group is said to be symmetric if it contains the inverses of all of its elements. Definition In set notation a subset S of a group G is called if whenever s \in S then the inverse of s also belongs to S. So if G is written multiplicatively then S is symmetric if and only if S = S^ where S^ := \left\. If G is written additively then S is symmetric if and only if S = - S where - S := \. If S is a subset of a vector space then S is said to be a if it is symmetric with respect to the additive group structure of the vector space; that is, if S = - S, which happens if and only if - S \subseteq S. The of a subset S is the smallest symmetric set containing S, and it is equal to S \cup - S. The largest symmetric set contained in S is S \cap - S. Sufficient conditions Arbitrary unions and intersections of symmetric sets are symmetric. Any vector subspace in a vector space is a symmetric set. Examples In \R, examples of symmetric s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A: P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Olive Jean Dunn
Olive Jean Dunn (1 September 1915 – 12 January 2008) was an American mathematician and statistician, and professor of biostatistics at the University of California Los Angeles (UCLA). She described methods for computing confidence intervals and also codified the Bonferroni correction's application to confidence intervals. She authored the textbook ''Basic Statistics: A Primer for the Biomedical Sciences'' in 1977. Education and career Dunn studied mathematics at the UCLA, earning a BA in 1936 and an MA in 1951. She was awarded a PhD in mathematics in 1956 at UCLA, supervised by Paul G. Hoel. The title of Dunn's doctoral dissertation was ''Estimation problems for dependent regression''. In 1956, she was appointed assistant professor of statistics at Iowa State College. Dunn returned to UCLA in 1959 as assistant professor of biostatistics and assistant professor of preventive medicine and health, later becoming full professor and serving in that role until her retirement. Du ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Royen
Thomas Royen (born 6 July 1947) is a retired German professor of statistics who has been affiliated with the University of Applied Sciences Bingen. Royen came to prominence in the spring of 2017 for a relatively simple proof for the Gaussian Correlation Inequality (GCI), a conjecture that originated in the 1950s, which he had published three years earlier without much recognition.Royen's proof of the Gaussian correlation inequality, arXiv:1512.08776/ref> A proof of this conjecture, which lies at the intersection of geometry, probability theory and statistics, had eluded top experts for decades. Life Youth, studies and private life Royen was born in 1947 to Paul Royen, a professor with the institute for inorganic chemistry at the Goethe University Frankfurt and Elisabeth Royen, also a chemist. From 1966 to 1971, he studied mathematics and physics at his father's university and the University of Freiburg. After graduating, he worked as a tutor at the University of Freiburg, be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
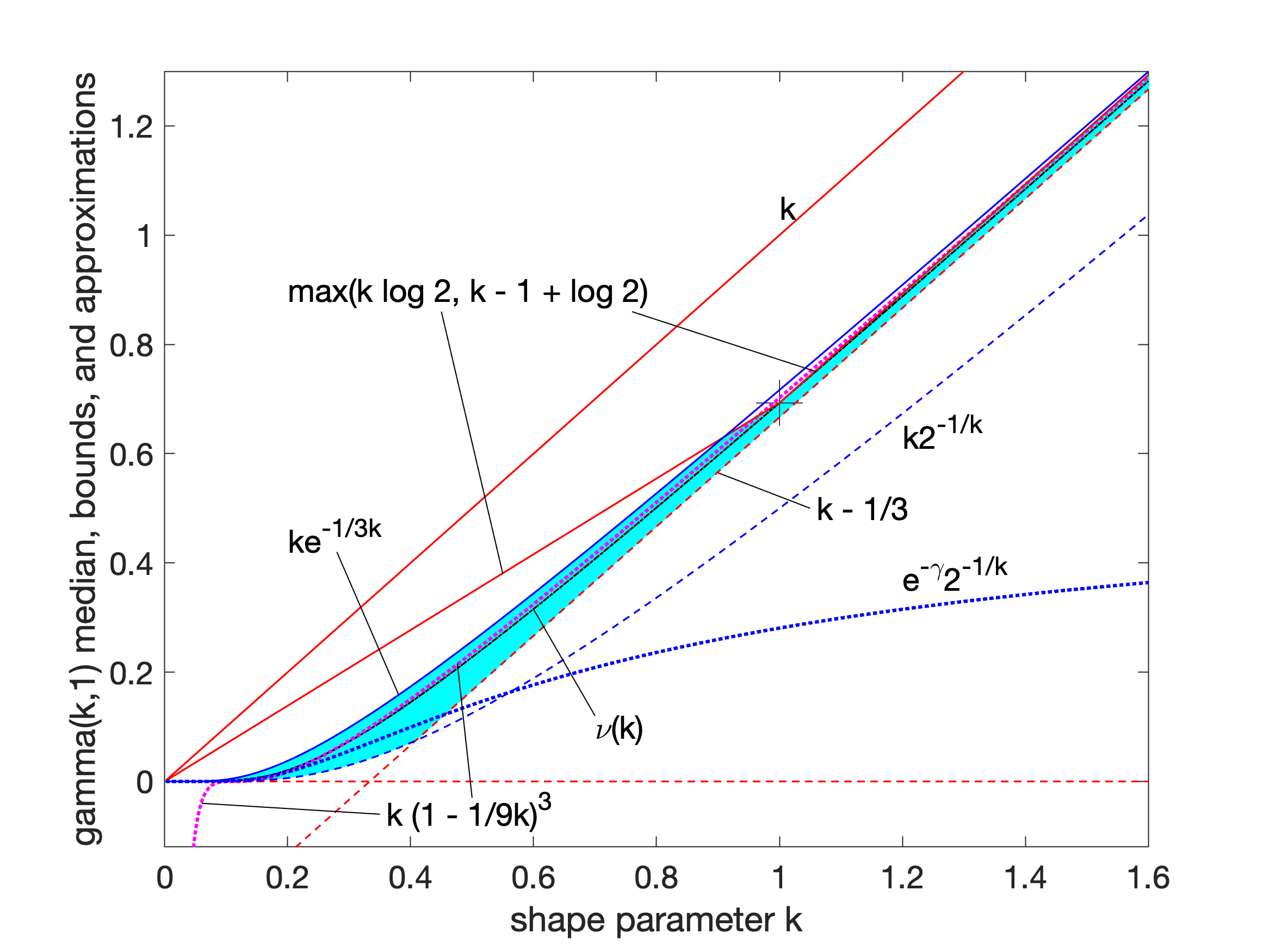
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common in econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predatory Journal
Predatory publishing, also write-only publishing or deceptive publishing, is an exploitative academic publishing business model that involves charging publication fees to authors without checking articles for quality and legitimacy, and without providing editorial and publishing services that legitimate academic journals provide, whether open access or not. The phenomenon of "open access predatory publishers" was first noticed by Jeffrey Beall, when he described "publishers that are ready to publish any article for payment". However, criticisms about the label "predatory" have been raised. A lengthy review of the controversy started by Beall appears in ''The Journal of Academic Librarianship''. Predatory publishers are so regarded because scholars are tricked into publishing with them, although some authors may be aware that the journal is poor quality or even fraudulent but publish in them anyway. New scholars from developing countries are said to be especially at risk of bein ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |