|
Grubbs's Test For Outliers
In statistics, Grubbs's test or the Grubbs test (named after Frank E. Grubbs, who published the test in 1950), also known as the maximum normalized residual test or extreme studentized deviate test, is a test used to detect outliers in a univariate data set assumed to come from a normally distributed population. Definition Grubbs's test is based on the assumption of normality. That is, one should first verify that the data can be reasonably approximated by a normal distribution before applying the Grubbs test. Grubbs's test detects one outlier at a time. This outlier is expunged from the dataset and the test is iterated until no outliers are detected. However, multiple iterations change the probabilities of detection, and the test should not be used for sample sizes of six or fewer since it frequently tags most of the points as outliers. Grubbs's test is defined for the following hypotheses: :H0: There are no outliers in the data set :Ha: There is exactly one outlier in the dat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frank E
Frank, FRANK, or Franks may refer to: People * Frank (given name) * Frank (surname) * Franks (surname) * Franks, a Germanic people in late Roman times * Franks, a term in the Muslim world for all western Europeans, particularly during the Crusades Currency * Liechtenstein franc or frank, the currency of Liechtenstein since 1920 * Swiss franc or frank, the currency of Switzerland since 1850 * Westphalian frank, currency of the Kingdom of Westphalia between 1808 and 1813 * The currencies of the German-speaking cantons of Switzerland (1803–1814): ** Appenzell frank ** Aargau frank ** Basel frank ** Berne frank ** Fribourg frank ** Glarus frank ** Graubünden frank ** Luzern frank ** Schaffhausen frank ** Schwyz frank ** Solothurn frank ** St. Gallen frank ** Thurgau frank ** Unterwalden frank ** Uri frank ** Zürich frank Places * Frank, Alberta, Canada, an urban community, formerly a village * Franks, Illinois, United States, an unincorporated community * Frank ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Value (statistics)
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe test of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tau Distribution
Tau (; uppercase Τ, lowercase τ or \boldsymbol\tau; ) is the nineteenth letter of the Greek alphabet, representing the voiceless dental or alveolar plosive . In the system of Greek numerals, it has a value of 300. The name in English is pronounced or , but in Greek it is . This is because the pronunciation of the combination of Greek letters αυ can have the pronunciation of either , or , depending on what follows and if a diaeresis is present on the second vowel (see Greek orthography). Tau was derived from the Phoenician letter taw (𐤕). Letters that arose from tau include Roman T and Cyrillic Te (Т, т). Modern usage The lower-case letter τ is used as a symbol for: * Specific tax amount Biology * The expressed period of the freerunning rhythm of an animal, i.e., the length of the daily cycle of an animal when kept in constant light or constant darkness * The dose interval in pharmacokinetics * The core variable in general tau theory * Tau in bioch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Studentized Residual
In statistics, a studentized residual is the dimensionless ratio resulting from the division of a errors and residuals in statistics, residual by an estimator, estimate of its standard deviation, both expressed in the same Unit of measurement, units. It is a form of a t-statistic, Student's ''t''-statistic, with the estimate of error varying between points. This is an important technique in the detection of outliers. It is among several named in honor of William Sealey Gosset, who wrote under the pseudonym "Student" (e.g., Student's distribution). Dividing a statistic by a sample standard deviation is called ''studentizing'', in analogy with ''standardizing'' and ''normalization (statistics), normalizing''. Motivation The key reason for studentizing is that, in regression analysis of a multivariate distribution, the variances of the ''residuals'' at different input variable values may differ, even if the variances of the ''errors'' at these different input variable values are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q Test
Q, or q, is the seventeenth letter of the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is pronounced , most commonly spelled ''cue'', but also ''kew'', ''kue'', and ''que''. History The Semitic sound value of Qôp was (voiceless uvular stop), and the form of the letter could have been based on the eye of a needle, a knot, or even a monkey with its tail hanging down. is a sound common to Semitic languages, but not found in many European languages. In common with other glyphs derived from the Proto-Sinaitic script, the letter has been suggested to have its roots in Egyptian hieroglyphs. In an early form of Ancient Greek, qoppa (Ϙ) probably came to represent several labialized velar stops, among them and . As a result of later sound shifts, these sounds in Greek changed to and respectively. Therefore, qoppa was transformed into two letters: qoppa, which stood for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peirce's Criterion
In robust statistics, Peirce's criterion is a rule for eliminating outliers from data sets, which was devised by Benjamin Peirce. Outliers removed by Peirce's criterion The problem of outliers In data sets containing real-numbered measurements, the suspected outliers are the measured values that appear to lie outside the cluster of most of the other data values. The outliers would greatly change the estimate of location if the arithmetic average were to be used as a summary statistic of location. The problem is that the arithmetic mean is very sensitive to the inclusion of any outliers; in statistical terminology, the arithmetic mean is not robust. In the presence of outliers, the statistician has two options. First, the statistician may remove the suspected outliers from the data set and then use the arithmetic mean to estimate the location parameter. Second, the statistician may use a robust statistic, such as the median statistic. Peirce's criterion is a statistical procedu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chauvenet's Criterion
In statistical theory, Chauvenet's criterion (named for William Chauvenet) is a means of assessing whether one piece of experimental data from a set of observations is likely to be spurious – an outlier. Derivation The idea behind Chauvenet's criterion finds a probability band that reasonably contains all ''n'' samples of a data set, centred on the mean of a normal distribution. By doing this, any data point from the ''n'' samples that lies outside this probability band can be considered an outlier, removed from the data set, and a new mean and standard deviation based on the remaining values and new sample size can be calculated. This identification of the outliers will be achieved by finding the number of standard deviations that correspond to the bounds of the probability band around the mean (D_) and comparing that value to the absolute value of the difference between the suspected outliers and the mean divided by the sample standard deviation (Eq.1). where * D_ is the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Probability Plot
The normal probability plot is a graphical technique to identify substantive departures from normality. This includes identifying outliers, skewness, kurtosis, a need for transformations, and mixtures. Normal probability plots are made of raw data, residuals from model fits, and estimated parameters. In a normal probability plot (also called a "normal plot"), the sorted data are plotted vs. values selected to make the resulting image look close to a straight line if the data are approximately normally distributed. Deviations from a straight line suggest departures from normality. The plotting can be manually performed by using a special graph paper, called ''normal probability paper''. With modern computers normal plots are commonly made with software. The normal probability plot is a special case of the Q–Q probability plot for a normal distribution. The theoretical quantiles are generally chosen to approximate either the mean or the median of the corresponding order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Histogram
A histogram is a visual representation of the frequency distribution, distribution of quantitative data. To construct a histogram, the first step is to Data binning, "bin" (or "bucket") the range of values— divide the entire range of values into a series of intervals—and then count how many values fall into each interval. The bins are usually specified as consecutive, non-overlapping interval (mathematics), intervals of a variable. The bins (intervals) are adjacent and are typically (but not required to be) of equal size. Histograms give a rough sense of the density of the underlying distribution of the data, and often for density estimation: estimating the probability density function of the underlying variable. The total area of a histogram used for probability density is always normalized to 1. If the length of the intervals on the ''x''-axis are all 1, then a histogram is identical to a relative frequency plot. Histograms are sometimes confused with bar charts. In a his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Box Plot
In descriptive statistics, a box plot or boxplot is a method for demonstrating graphically the locality, spread and skewness groups of numerical data through their quartiles. In addition to the box on a box plot, there can be lines (which are called ''whiskers'') extending from the box indicating variability outside the upper and lower quartiles, thus, the plot is also called the box-and-whisker plot and the box-and-whisker diagram. Outliers that differ significantly from the rest of the dataset may be plotted as individual points beyond the whiskers on the box-plot. Box plots are non-parametric: they display variation in samples of a statistical population without making any assumptions of the underlying probability distribution, statistical distribution (though Tukey's boxplot assumes symmetry for the whiskers and normality for their length). The spacings in each subsection of the box-plot indicate the degree of statistical dispersion, dispersion (spread) and skewness of the da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
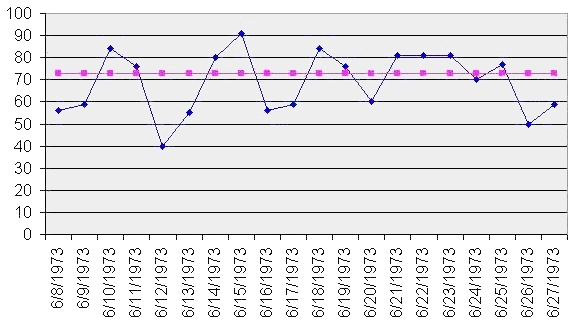
Run Sequence Plot
A run chart, also known as a run-sequence plot is a graph that displays observed data in a time sequence. Often, the data displayed represent some aspect of the output or performance of a manufacturing or other business process. It is therefore a form of line chart. Overview Run sequence plots are an easy way to graphically summarize a univariate data set. A common assumption of univariate data sets is that they behave like:NIST/SEMATECH (2003)"Run-Sequence Plot"In: ''e-Handbook of Statistical Methods'' 6/01/2003 (Date created). * random drawings; * from a fixed distribution; * with a common location; and * with a common scale. With run sequence plots, shifts in location and scale are typically quite evident. Also, outliers can easily be detected. Examples could include measurements of the fill level of bottles filled at a bottling plant or the water temperature of a dishwashing machine each time it is run. Time is generally represented on the horizontal (x) axis and the pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphical Technique
Statistical graphics, also known as statistical graphical techniques, are graphics used in the field of statistics for data visualization. Overview Whereas statistics and data analysis procedures generally yield their output in numeric or tabular form, graphical techniques allow such results to be displayed in some sort of pictorial form. They include plots such as scatter plots, histograms, probability plots, spaghetti plots, residual plots, box plots, block plots and biplots. Exploratory data analysis (EDA) relies heavily on such techniques. They can also provide insight into a data set to help with testing assumptions, model selection and regression model validation, estimator selection, relationship identification, factor effect determination, and outlier detection. In addition, the choice of appropriate statistical graphics can provide a convincing means of communicating the underlying message that is present in the data to others. Graphical statistical methods have fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |