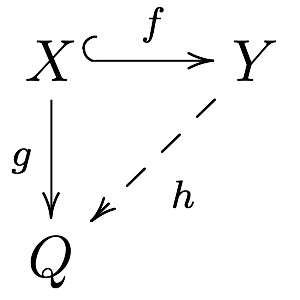|
Grothendieck's Tôhoku Paper
The article "Sur quelques points d'algèbre homologique" by Alexander Grothendieck, now often referred to as the ''Tôhoku'' paper, was published in 1957 in the '' Tôhoku Mathematical Journal''. It has revolutionized the subject of homological algebra, a purely algebraic aspect of algebraic topology. It removed the need to distinguish the cases of modules over a ring and sheaves of abelian groups over a topological space. Background Material in the paper dates from Grothendieck's year at the University of Kansas in 1955–6. Research there allowed him to put homological algebra on an axiomatic basis, by introducing the abelian category concept. A textbook treatment of homological algebra, "Cartan–Eilenberg" after the authors Henri Cartan and Samuel Eilenberg, appeared in 1956. Grothendieck's work was largely independent of it. His abelian category concept had at least partially been anticipated by others. David Buchsbaum in his doctoral thesis written under Eilenberg had int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enough Injectives
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent Duality
In mathematics, coherent duality is any of a number of generalisations of Serre duality, applying to coherent sheaves, in algebraic geometry and complex manifold theory, as well as some aspects of commutative algebra that are part of the 'local' theory. The historical roots of the theory lie in the idea of the adjoint linear system of a linear system of divisors in classical algebraic geometry. This was re-expressed, with the advent of sheaf theory, in a way that made an analogy with Poincaré duality more apparent. Then according to a general principle, Grothendieck's relative point of view, the theory of Jean-Pierre Serre was extended to a proper morphism; Serre duality was recovered as the case of the morphism of a non-singular projective variety (or complete variety) to a point. The resulting theory is now sometimes called Serre–Grothendieck–Verdier duality, and is a basic tool in algebraic geometry. A treatment of this theory, ''Residues and Duality'' (1966) by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Congress Of Mathematicians
The International Congress of Mathematicians (ICM) is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union (IMU). The Fields Medals, the Nevanlinna Prize (to be renamed as the IMU Abacus Medal), the Gauss Prize, and the Chern Medal are awarded during the congress's opening ceremony. Each congress is memorialized by a printed set of Proceedings recording academic papers based on invited talks intended to be relevant to current topics of general interest. Being invited to talk at the ICM has been called "the equivalent ... of an induction to a hall of fame". History Felix Klein and Georg Cantor are credited with putting forward the idea of an international congress of mathematicians in the 1890s.A. John Coleman"Mathematics without borders": a book review ''CMS Notes'', vol 31, no. 3, April 1999, pp. 3-5 The University of Chicago, which had opened in 1892, organized an International Mathematical Con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derived Category
In mathematics, the derived category ''D''(''A'') of an abelian category ''A'' is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on ''A''. The construction proceeds on the basis that the objects of ''D''(''A'') should be chain complexes in ''A'', with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequences. The development of the derived category, by Alexander Grothendieck and his student Jean-Louis Verdier shortly after 1960, now appears as one terminal point in the explosive development of homological algebra in the 1950s, a decade in which it had made re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean-Louis Verdier
Jean-Louis Verdier (; 2 February 1935 – 25 August 1989) was a French mathematician who worked, under the guidance of his doctoral advisor Alexander Grothendieck, on derived categories and Verdier duality. He was a close collaborator of Grothendieck, notably contributing to SGA 4 his theory of hypercovers and anticipating the later development of étale homotopy by Michael Artin and Barry Mazur, following a suggestion he attributed to Pierre Cartier. Saul Lubkin's related theory of rigid hypercovers was later taken up by Eric Friedlander in his definition of the étale topological type. Verdier was a student at the elite École Normale Supérieure in Paris, and later became director of studies there, as well as a Professor at the University of Paris VII. For many years he directed a joint seminar at the École Normale Supérieure with Adrien Douady. Verdier was a member of Bourbaki. In 1984 he was the president of the Société Mathématique de France. In 1976 Verdie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derived Functor
In mathematics, certain functors may be ''derived'' to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics. Motivation It was noted in various quite different settings that a short exact sequence often gives rise to a "long exact sequence". The concept of derived functors explains and clarifies many of these observations. Suppose we are given a covariant left exact functor ''F'' : A → B between two abelian categories A and B. If 0 → ''A'' → ''B'' → ''C'' → 0 is a short exact sequence in A, then applying ''F'' yields the exact sequence 0 → ''F''(''A'') → ''F''(''B'') → ''F''(''C'') and one could ask how to continue this sequence to the right to form a long exact sequence. Strictly speaking, this question is ill-posed, since there are always numerous different ways to continue a given exact sequence to the right. But it turns out that (if A is "nice" enough) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grothendieck Spectral Sequence
In mathematics, in the field of homological algebra, the Grothendieck spectral sequence, introduced by Alexander Grothendieck in his ''Tôhoku'' paper, is a spectral sequence that computes the derived functors of the composition of two functors G\circ F, from knowledge of the derived functors of F and G. Many spectral sequences in algebraic geometry are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence. Statement If F \colon\mathcal\to\mathcal and G \colon \mathcal\to\mathcal are two additive and left exact functors between abelian categories such that both \mathcal and \mathcal have enough injectives and F takes injective objects to G- acyclic objects, then for each object A of \mathcal there is a spectral sequence: :E_2^ = (^p G \circ^q F)(A) \Longrightarrow ^ (G\circ F)(A), where ^p G denotes the ''p''-th right-derived functor of G, etc., and where the arrow '\Longrightarrow' means convergence of spectral sequences. Five term e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Module Category
In algebra, given a ring ''R'', the category of left modules over ''R'' is the category whose objects are all left modules over ''R'' and whose morphisms are all module homomorphisms between left ''R''-modules. For example, when ''R'' is the ring of integers Z, it is the same thing as the category of abelian groups. The category of right modules is defined in a similar way. Note: Some authors use the term module category for the category of modules. This term can be ambiguous since it could also refer to a category with a monoidal-category action. Properties The categories of left and right modules are abelian categories. These categories have enough projectives and enough injectives. Mitchell's embedding theorem states every abelian category arises as a full subcategory of the category of modules. Projective limits and inductive limits exist in the categories of left and right modules. Over a commutative ring, together with the tensor product of modules ⊗, the category ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Of An Abelian Category
In mathematics, the quotient (also called Serre quotient or Gabriel quotient) of an abelian category \mathcal by a Serre subcategory \mathcal is the abelian category \mathcal/\mathcal which, intuitively, is obtained from \mathcal by ignoring (i.e. treating as zero) all objects from \mathcal. There is a canonical exact functor Q \colon \mathcal \to \mathcal/\mathcal whose kernel is \mathcal B, and \mathcal/\mathcal is in a certain sense the most general abelian category with this property. Forming Serre quotients of abelian categories is thus formally akin to forming quotients of groups. Serre quotients are somewhat similar to quotient categories, the difference being that with Serre quotients all involved categories are abelian and all functors are exact. Serre quotients also often have the character of localizations of categories, especially if the Serre subcategory is localizing. Definition Formally, \mathcal A/\mathcal B is the category whose objects are those of \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gabriel–Popescu Theorem
In mathematics, the Gabriel–Popescu theorem is an embedding theorem for certain abelian categories, introduced by . It characterizes certain abelian categories (the Grothendieck categories) as quotients of module categories. There are several generalizations and variations of the Gabriel–Popescu theorem, given by (for an AB5 category with a set of generators), , (for triangulated categories). Theorem Let ''A'' be a Grothendieck category (an AB5 category with a generator), ''G'' a generator of ''A'' and ''R'' be the ring of endomorphisms of ''G''; also, let ''S'' be the functor from ''A'' to Mod-''R'' (the category of right ''R''-modules) defined by ''S''(''X'') = Hom(''G'',''X''). Then the Gabriel–Popescu theorem states that ''S'' is full and faithful and has an exact left adjoint. This implies that ''A'' is equivalent to the Serre quotient category of Mod-''R'' by a certain localizing subcategory ''C''. (A localizing subcategory of Mod-''R'' is a full subcategory '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cohomology Theory
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory. From its beginning in topology, this idea became a dominant method in the mathematics of the second half of the twentieth century. From the initial idea of homology as a method of constructing algebraic invariants of topological spaces, the range of applications of homology and cohomology theories has spread throughout geometry and algebra. The terminology tends to hide the fact that cohomology, a contravariant theory, is more natural than homology in many applications. At a basic level, this has to do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |