|
Graph Kernel
In structure mining, a graph kernel is a kernel function that computes an inner product on graphs. Graph kernels can be intuitively understood as functions measuring the similarity of pairs of graphs. They allow kernelized learning algorithms such as support vector machines to work directly on graphs, without having to do feature extraction to transform them to fixed-length, real-valued feature vectors. They find applications in bioinformatics, in chemoinformatics (as a type of molecule kernels), and in social network analysis. Concepts of graph kernels have been around since the 1999, when D. Haussler introduced convolutional kernels on discrete structures. The term graph kernels was more officially coined in 2002 by R. I. Kondor and J. Lafferty as kernels ''on'' graphs, i.e. similarity functions between the nodes of a single graph, with the World Wide Web hyperlink graph as a suggested application. In 2003, Gaertner ''et al.'' and Kashima ''et al.'' defined kernels ''betwee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure Mining
Structure mining or structured data mining is the process of finding and extracting useful information from semi-structured data sets. Graph mining, sequential pattern mining and molecule mining are special cases of structured data mining. Description The growth of the use of semi-structured data has created new opportunities for data mining, which has traditionally been concerned with tabular data sets, reflecting the strong association between data mining and relational databases. Much of the world's interesting and mineable data does not easily fold into relational databases, though a generation of software engineers have been trained to believe this was the only way to handle data, and data mining algorithms have generally been developed only to cope with tabular data. XML, being the most frequent way of representing semi-structured data, is able to represent both tabular data and arbitrary trees. Any particular representation of data to be exchanged between two applications i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
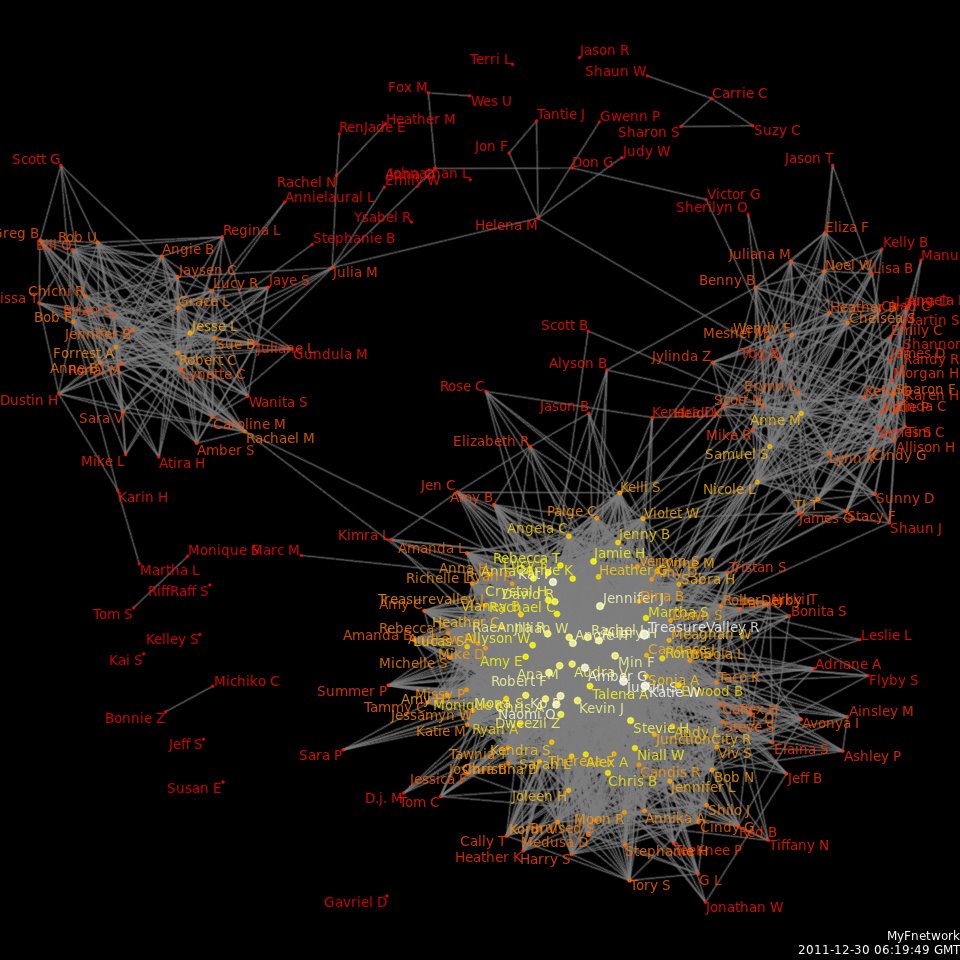
Social Network Analysis
Social network analysis (SNA) is the process of investigating social structures through the use of networks and graph theory. It characterizes networked structures in terms of ''nodes'' (individual actors, people, or things within the network) and the ''ties'', ''edges'', or ''links'' (relationships or interactions) that connect them. Examples of social structures commonly visualized through social network analysis include social media networks, memes spread, information circulation, friendship and acquaintance networks, business networks, knowledge networks, difficult working relationships, social networks, collaboration graphs, kinship, disease transmission, and sexual relationships. These networks are often visualized through '' sociograms'' in which nodes are represented as points and ties are represented as lines. These visualizations provide a means of qualitatively assessing networks by varying the visual representation of their nodes and edges to reflect attribute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecule Mining
This page describes mining for molecules. Since molecules may be represented by molecular graphs this is strongly related to graph mining and structured data mining. The main problem is how to represent molecules while discriminating the data instances. One way to do this is chemical similarity metrics, which has a long tradition in the field of cheminformatics. Typical approaches to calculate chemical similarities use chemical fingerprints, but this loses the underlying information about the molecule topology. Mining the molecular graphs directly avoids this problem. So does the inverse QSAR problem which is preferable for vectorial mappings. Coding(Moleculei,Moleculej\neqi) Kernel methods * Marginalized graph kernelH. Kashima, K. Tsuda, A. Inokuchi, Marginalized Kernels Between Labeled Graphs, The 20th International Conference on Machine Learning (ICML2003), 2003. PDF * Optimal assignment kernelH. Fröhlich, J. K. Wegner, A. Zell, ''Optimal Assignment Kernels For Attrib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tree Kernel
In machine learning, tree kernels are the application of the more general concept of positive-definite kernel to tree structures. They find applications in natural language processing, where they can be used for machine-learned parsing or classification of sentences. Motivation In natural language processing, it is often necessary to compare tree structures (e.g. parse trees) for similarity. Such comparisons can be performed by computing dot products of vectors of features of the trees, but these vectors tend to be very large: NLP techniques have come to a point where a simple dependency relation over two words is encoded with a vector of several millions of features. It can be impractical to represent complex structures such as trees with features vectors. Well-designed kernels allow computing similarity over trees without explicitly computing the feature vectors of these trees. Moreover, kernel methods have been widely used in machine learning tasks (e.g. SVM), and thus plenty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product Of Graphs
In graph theory, the tensor product of graphs and is a graph such that * the vertex set of is the Cartesian product ; and * vertices and are adjacent in if and only if ** is adjacent to in , and ** is adjacent to in . The tensor product is also called the direct product, Kronecker product, categorical product, cardinal product, relational product, weak direct product, or conjunction. As an operation on binary relations, the tensor product was introduced by Alfred North Whitehead and Bertrand Russell in their Principia Mathematica (1912). It is also equivalent to the Kronecker product of the adjacency matrices of the graphs. The notation is also (and formerly normally was) used to represent another construction known as the Cartesian product of graphs, but nowadays more commonly refers to the tensor product. The cross symbol shows visually the two edges resulting from the tensor product of two edges. This product should not be confused with the strong product of gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path (graph Theory)
In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct (and since the vertices are distinct, so are the edges). A directed path (sometimes called dipathGraph Structure Theory: Proceedings of the AMS-IMS-SIAM Joint Summer Research Conference on Graph Minors, Held June 22 to July 5, 1991p.205/ref>) in a directed graph is a finite or infinite sequence of edges which joins a sequence of distinct vertices, but with the added restriction that the edges be all directed in the same direction. Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See e.g. Bondy and Murty (1976), Gibbons (1985), or Diestel (2005). Korte et al. (1990) cover more advanced algorithmic topics concerning paths in graphs. Definitions Walk, trail, and path * A walk is a finite or infinite sequence of edges which joins a sequence of vertices. : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Lattice random walk A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperlink
In computing, a hyperlink, or simply a link, is a digital reference to data that the user can follow or be guided by clicking or tapping. A hyperlink points to a whole document or to a specific element within a document. Hypertext is text with hyperlinks. The text that is linked from is known as anchor text. A software system that is used for viewing and creating hypertext is a ''hypertext system'', and to create a hyperlink is ''to hyperlink'' (or simply ''to link''). A user following hyperlinks is said to ''navigate'' or ''browse'' the hypertext. The document containing a hyperlink is known as its source document. For example, in an online reference work such as Wikipedia or Google, many words and terms in the text are hyperlinked to definitions of those terms. Hyperlinks are often used to implement reference mechanisms such as tables of contents, footnotes, bibliographies, indexes, letters, and glossaries. In some hypertext, hyperlinks can be bidirectional: they c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
World Wide Web
The World Wide Web (WWW), commonly known as the Web, is an information system enabling documents and other web resources to be accessed over the Internet. Documents and downloadable media are made available to the network through web servers and can be accessed by programs such as web browsers. Servers and resources on the World Wide Web are identified and located through character strings called uniform resource locators (URLs). The original and still very common document type is a web page formatted in Hypertext Markup Language (HTML). This markup language supports plain text, digital image, images, embedded video and audio signal, audio contents, and scripting language, scripts (short programs) that implement complex user interaction. The HTML language also supports hyperlinks (embedded URLs) which provide immediate access to other web resources. Web navigation, or web surfing, is the common practice of following such hyperlinks across multiple websites. Web applicatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John D
John is a common English name and surname: * John (given name) * John (surname) John may also refer to: New Testament Works * Gospel of John, a title often shortened to John * First Epistle of John, often shortened to 1 John * Second Epistle of John, often shortened to 2 John * Third Epistle of John, often shortened to 3 John People * John the Baptist (died c. AD 30), regarded as a prophet and the forerunner of Jesus Christ * John the Apostle (lived c. AD 30), one of the twelve apostles of Jesus * John the Evangelist, assigned author of the Fourth Gospel, once identified with the Apostle * John of Patmos, also known as John the Divine or John the Revelator, the author of the Book of Revelation, once identified with the Apostle * John the Presbyter, a figure either identified with or distinguished from the Apostle, the Evangelist and John of Patmos Other people with the given name Religious figures * John, father of Andrew the Apostle and Saint Peter * Po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecule Kernel
This page describes mining for molecules. Since molecules may be represented by molecular graphs this is strongly related to graph mining and structured data mining. The main problem is how to represent molecules while discriminating the data instances. One way to do this is chemical similarity metrics, which has a long tradition in the field of cheminformatics. Typical approaches to calculate chemical similarities use chemical fingerprints, but this loses the underlying information about the molecule topology. Mining the molecular graphs directly avoids this problem. So does the inverse QSAR problem which is preferable for vectorial mappings. Coding(Moleculei,Moleculej\neqi) Kernel methods * Marginalized graph kernelH. Kashima, K. Tsuda, A. Inokuchi, Marginalized Kernels Between Labeled Graphs, The 20th International Conference on Machine Learning (ICML2003), 2003. PDF * Optimal assignment kernelH. Fröhlich, J. K. Wegner, A. Zell, ''Optimal Assignment Kernels For Attribute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Kernel
In operator theory, a branch of mathematics, a positive-definite kernel is a generalization of a positive-definite function or a positive-definite matrix. It was first introduced by James Mercer in the early 20th century, in the context of solving integral operator equations. Since then, positive-definite functions and their various analogues and generalizations have arisen in diverse parts of mathematics. They occur naturally in Fourier analysis, probability theory, operator theory, complex function-theory, moment problems, integral equations, boundary-value problems for partial differential equations, machine learning, embedding problem, information theory, and other areas. This article will discuss some of the historical and current developments of the theory of positive-definite kernels, starting with the general idea and properties before considering practical applications. Definition Let \mathcal X be a nonempty set, sometimes referred to as the index set. A symme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |