|
Gram–Schmidt Process
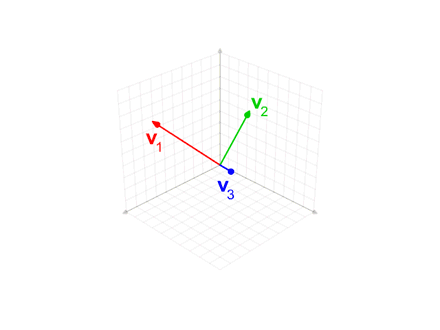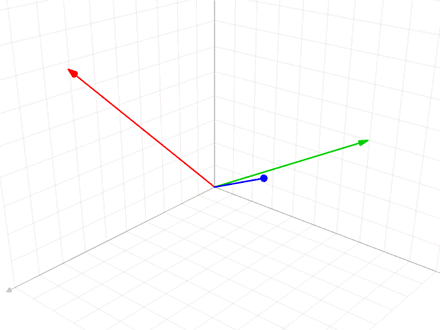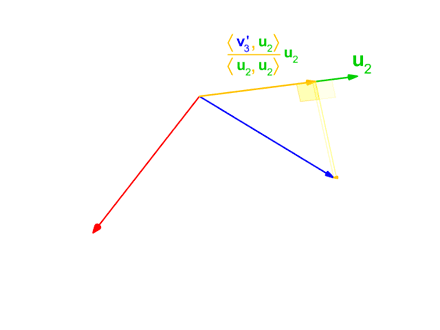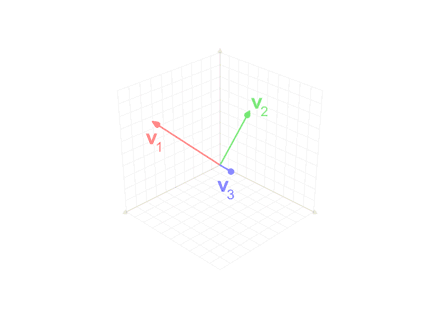
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other. By technical definition, it is a method of constructing an orthonormal basis from a set of vector (geometry), vectors in an inner product space, most commonly the Euclidean space \mathbb^n equipped with the standard inner product. The Gram–Schmidt process takes a finite set, finite, linearly independent set of vectors S = \ for and generates an orthogonal set S' = \ that spans the same k-dimensional subspace of \mathbb^n as S. The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition. The application of the Gram–Schmidt process to the column vectors of a full column rank (linear algebra), rank mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rank (linear Algebra)
In linear algebra, the rank of a matrix is the dimension of the vector space generated (or spanned) by its columns. p. 48, § 1.16 This corresponds to the maximal number of linearly independent columns of . This, in turn, is identical to the dimension of the vector space spanned by its rows. Rank is thus a measure of the " nondegenerateness" of the system of linear equations and linear transformation encoded by . There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics. The rank is commonly denoted by or ; sometimes the parentheses are not written, as in .Alternative notation includes \rho (\Phi) from and . Main definitions In this section, we give some definitions of the rank of a matrix. Many definitions are possible; see Alternative definitions for several of these. The column rank of is the dimension of the column space of , while the row rank of is the dimension of the row space of . A fundamental resul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Countably Infinite
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (the number of elements of the set) is not greater than that of the natural numbers. A countable set that is not finite is said to be countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Induction
Mathematical induction is a method for mathematical proof, proving that a statement P(n) is true for every natural number n, that is, that the infinitely many cases P(0), P(1), P(2), P(3), \dots all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for n = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case n = k, ''then'' it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. The base case does not necessarily begin with n = 0, but often with n = 1, and possibly with any fixed natural number n = N, establishing the trut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthonormalization
In linear algebra, orthogonalization is the process of finding a Set (mathematics), set of orthogonal vectors that span (linear algebra), span a particular linear subspace, subspace. Formally, starting with a linearly independent set of vectors in an inner product space (most commonly the Euclidean space R''n''), orthogonalization results in a set of Orthogonality, orthogonal vectors that Generator (mathematics), generate the same subspace as the vectors ''v''1, ... , ''v''''k''. Every vector in the new set is orthogonal to every other vector in the new set; and the new set and the old set have the same linear span. In addition, if we want the resulting vectors to all be unit vectors, then we Unit vector, normalize each vector and the procedure is called orthonormalization. Orthogonalization is also possible with respect to any symmetric bilinear form (not necessarily an inner product, not necessarily over real numbers), but standard algorithms may encounter div ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthogonalization
In linear algebra, orthogonalization is the process of finding a set of orthogonal vectors that span a particular subspace. Formally, starting with a linearly independent set of vectors in an inner product space (most commonly the Euclidean space R''n''), orthogonalization results in a set of orthogonal vectors that generate the same subspace as the vectors ''v''1, ... , ''v''''k''. Every vector in the new set is orthogonal to every other vector in the new set; and the new set and the old set have the same linear span. In addition, if we want the resulting vectors to all be unit vectors, then we normalize each vector and the procedure is called orthonormalization. Orthogonalization is also possible with respect to any symmetric bilinear form (not necessarily an inner product, not necessarily over real numbers), but standard algorithms may encounter division by zero in this more general setting. Orthogonalization algorithms Methods for performing orthogona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthonormal Set
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal unit vectors. A unit vector means that the vector has a length of 1, which is also known as normalized. Orthogonal means that the vectors are all perpendicular to each other. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length. An orthonormal set which forms a basis is called an ''orthonormal basis''. Intuitive overview The construction of orthogonality of vectors is motivated by a desire to extend the intuitive notion of perpendicular vectors to higher-dimensional spaces. In the Cartesian plane, two vectors are said to be ''perpendicular'' if the angle between them is 90° (i.e. if they form a right angle). This definition can be formalized in Cartesian space by defining the dot product and specifying that two vectors in the plane are orthogonal if their dot product is zero. Similarly, the construction of the norm of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |