|
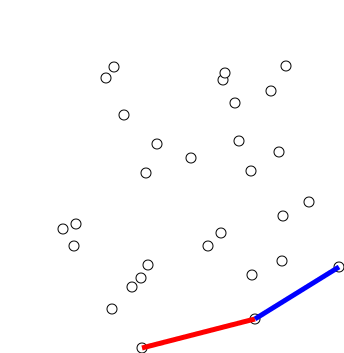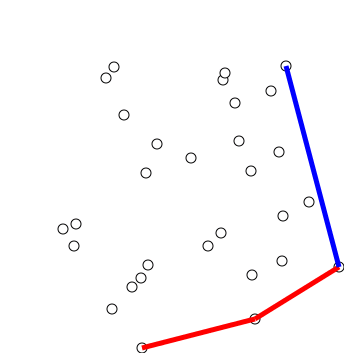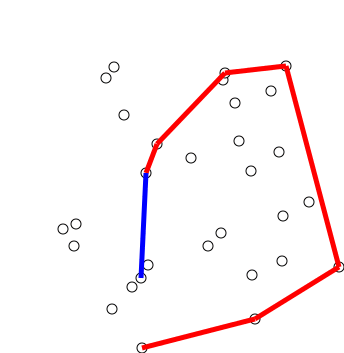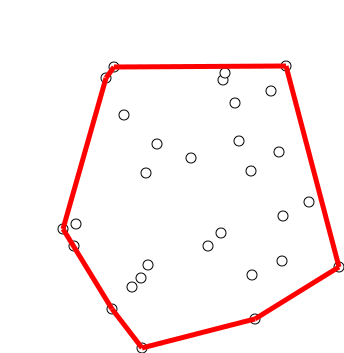
Graham Scan
Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(''n'' log ''n''). It is named after Ronald Graham, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently. Algorithm The first step in this algorithm is to find the point with the lowest y-coordinate. If the lowest y-coordinate exists in more than one point in the set, the point with the lowest x-coordinate out of the candidates should be chosen. Call this point ''P''. This step takes O(''n''), where ''n'' is the number of points in question. Next, the set of points must be sorted in increasing order of the angle they and the point ''P'' make with the x-axis. Any general-purpose sorting algorithm is appropriate for this, for example heapsort (which is O(''n'' log ''n'')). Sorting in order of angle does not require ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Introduction To Algorithms
''Introduction to Algorithms'' is a book on computer programming by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The book has been widely used as the textbook for algorithms courses at many universities and is commonly cited as a reference for algorithms in published papers, with over 10,000 citations documented on CiteSeerX. The book sold half a million copies during its first 20 years. Its fame has led to the common use of the abbreviation "CLRS" (Cormen, Leiserson, Rivest, Stein), or, in the first edition, "CLR" (Cormen, Leiserson, Rivest). In the preface, the authors write about how the book was written to be comprehensive and useful in both teaching and professional environments. Each chapter focuses on an algorithm, and discusses its design techniques and areas of application. Instead of using a specific programming language, the algorithms are written in pseudocode. The descriptions focus on the aspects of the algorithm itself, its ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull Algorithms
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science. In computational geometry, numerous algorithms are proposed for computing the convex hull of a finite set of points, with various computational complexities. Computing the convex hull means that a non-ambiguous and efficient representation of the required convex shape is constructed. The complexity of the corresponding algorithms is usually estimated in terms of ''n'', the number of input points, and sometimes also in terms of ''h'', the number of points on the convex hull. Planar case Consider the general case when the input to the algorithm is a finite unordered set of points on a Cartesian plane. An important special case, in which the points are given in the order of traversal of a simple polygon's boundary, is described later in a separate subsection. If not all points are on the same line, then their convex hull is a convex polygon whose ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steven Fortune
Stephen or Steven is a common English first name. It is particularly significant to Christians, as it belonged to Saint Stephen ( grc-gre, Στέφανος ), an early disciple and deacon who, according to the Book of Acts, was stoned to death; he is widely regarded as the first martyr (or "protomartyr") of the Christian Church. In English, Stephen is most commonly pronounced as ' (). The name, in both the forms Stephen and Steven, is often shortened to Steve or Stevie. The spelling as Stephen can also be pronounced which is from the Greek original version, Stephanos. In English, the female version of the name is Stephanie. Many surnames are derived from the first name, including Stephens, Stevens, Stephenson, and Stevenson, all of which mean "Stephen's (son)". In modern times the name has sometimes been given with intentionally non-standard spelling, such as Stevan or Stevon. A common variant of the name used in English is Stephan ; related names that have found some curre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-conditioned
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem: given f(x) = y, one is solving for ''x,'' and thus the condition number of the (local) inverse must be used. In linear regression the condition number of the moment matrix can be used as a diagnostic for multicollinearity. The condition number is an application of the derivative, and is formally defined as the value of the asymptotic worst-case relative change in output for a relative change in input. The "function" is the solution of a problem and the "arguments" are the data in the problem. The condition number is frequently applied to questions in linear algebra, in which case the derivative is straightforward b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backward Error Analysis
In mathematics, error analysis is the study of kind and quantity of error, or uncertainty, that may be present in the solution to a problem. This issue is particularly prominent in applied areas such as numerical analysis and statistics. Error analysis in numerical modeling In numerical simulation or modeling of real systems, error analysis is concerned with the changes in the output of the model as the parameters to the model vary about a mean. For instance, in a system modeled as a function of two variables z \,=\, f(x,y). Error analysis deals with the propagation of the numerical errors in x and y (around mean values \bar and \bar) to error in z (around a mean \bar). In numerical analysis, error analysis comprises both forward error analysis and backward error analysis. Forward error analysis Forward error analysis involves the analysis of a function z' = f'(a_0,\,a_1,\,\dots,\,a_n) which is an approximation (usually a finite polynomial) to a function z \,=\, f(a_0,a_1,\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lecture Notes In Computer Science
''Lecture Notes in Computer Science'' is a series of computer science books published by Springer Science+Business Media since 1973. Overview The series contains proceedings, post- proceedings, monographs, and Festschrift In academia, a ''Festschrift'' (; plural, ''Festschriften'' ) is a book honoring a respected person, especially an academic, and presented during their lifetime. It generally takes the form of an edited volume, containing contributions from the ...s. In addition, tutorials, state-of-the-art surveys, and "hot topics" are increasingly being included. The series is indexed by DBLP. See also *'' Monographiae Biologicae'', another monograph series published by Springer Science+Business Media *'' Lecture Notes in Physics'' *'' Lecture Notes in Mathematics'' *'' Electronic Workshops in Computing'', published by the British Computer Society References External links * Publications established in 1973 Computer science books Series of non-fiction books ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity. Computational complexity is central to computational geometry, with great practical significance if algorithms are used on very large datasets containing tens or hundreds of millions of points. For such sets, the difference between O(''n''2) and O(''n'' log ''n'') may be the difference between days and seconds of computation. The main impetus for the development of computational geometry as a discipline was progress in computer graphics and computer-aided design and manufacturing (CAD/CAM), but many problems in computational geometry ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floating-point
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be represented as a base-ten floating-point number: 12.345 = \underbrace_\text \times \underbrace_\text\!\!\!\!\!\!^ In practice, most floating-point systems use base two, though base ten ( decimal floating point) is also common. The term ''floating point'' refers to the fact that the number's radix point can "float" anywhere to the left, right, or between the significant digits of the number. This position is indicated by the exponent, so floating point can be considered a form of scientific notation. A floating-point system can be used to represent, with a fixed number of digits, numbers of very different orders of magnitude — such as the number of meters between galaxies or between protons in an atom. For this reason, floating-p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Robustness
In computer science, robustness is the ability of a computer system to cope with errors during execution1990. IEEE Standard Glossary of Software Engineering Terminology, IEEE Std 610.12-1990 defines robustness as "The degree to which a system or component can function correctly in the presence of invalid inputs or stressful environmental conditions" and cope with erroneous input. Robustness can encompass many areas of computer science, such as robust programming, robust machine learning, and Robust Security Network. Formal techniques, such as fuzz testing, are essential to showing robustness since this type of testing involves invalid or unexpected inputs. Alternatively, fault injection can be used to test robustness. Various commercial products perform robustness testing of software analysis. Introduction In general, building robust systems that encompass every point of possible failure is difficult because of the vast quantity of possible inputs and input combinations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
All Nearest Smaller Values
In computer science, the all nearest smaller values problem is the following task: for each position in a sequence of numbers, search among the previous positions for the last position that contains a smaller value. This problem can be solved efficiently both by parallel and non-parallel algorithms: , who first identified the procedure as a useful subroutine for other parallel programs, developed efficient algorithms to solve it in the Parallel Random Access Machine model; it may also be solved in linear time on a non-parallel computer using a stack-based algorithm. Later researchers have studied algorithms to solve it in other models of parallel computation. Example Suppose that the input is the binary van der Corput sequence :0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15. The first element of the sequence (0) has no previous value. The nearest (only) smaller value previous to 8 and to 4 is 0. All three values previous to 12 are smaller, but the nearest one is 4. Continuin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygonalization
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle. Every point set that does not lie on a single line has at least one polygonalization, which can be found in polynomial time. For points in convex position, there is only one, but for some other point sets there can be exponentially many. Finding an optimal polygonalization under several natural optimization criteria is a hard problem, including as a special case the travelling salesman problem. The complexity of counting all polygonalizations remains unknown. Definition A polygonalization is a simple polygon having a given set of points in the Euclidean plane as its set of vertices. A polygon may be described by a cyclic order on its vertices, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |