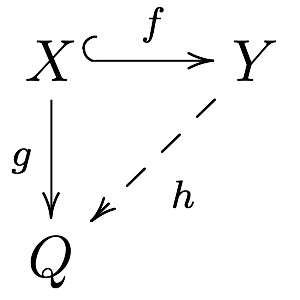|
Giraud Subcategory
In mathematics, Giraud subcategories form an important class of subcategories of Grothendieck categories. They are named after Jean Giraud. Definition Let \mathcal be a Grothendieck category. A full subcategory \mathcal is called ''reflective'', if the inclusion functor i\colon\mathcal\rightarrow\mathcal has a left adjoint. If this left adjoint of i also preserves kernels, then \mathcal is called a ''Giraud subcategory''. Properties Let \mathcal be Giraud in the Grothendieck category \mathcal and i\colon\mathcal\rightarrow\mathcal the inclusion functor. * \mathcal is again a Grothendieck category. * An object X in \mathcal is injective if and only if i(X) is injective in \mathcal. * The left adjoint a\colon\mathcal\rightarrow\mathcal of i is exact. * Let \mathcal be a localizing subcategory of \mathcal and \mathcal/\mathcal be the associated quotient category In mathematics, a quotient category is a category obtained from another one by identifying sets of morphisms. Formal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grothendieck Category
In mathematics, a Grothendieck category is a certain kind of abelian category, introduced in Alexander Grothendieck's Tôhoku paper of 1957English translation in order to develop the machinery of homological algebra for modules and for sheaves in a unified manner. The theory of these categories was further developed in Pierre Gabriel's seminal thesis in 1962. To every algebraic variety V one can associate a Grothendieck category \operatorname(V), consisting of the quasi-coherent sheaves on V. This category encodes all the relevant geometric information about V, and V can be recovered from \operatorname(V) (the Gabriel–Rosenberg reconstruction theorem). This example gives rise to one approach to noncommutative algebraic geometry: the study of "non-commutative varieties" is then nothing but the study of (certain) Grothendieck categories. Definition By definition, a Grothendieck category \mathcal is an AB5 category with a generator. Spelled out, this means that * \mathcal is an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean Giraud (mathematician)
Jean Giraud (; 2 February 1936 – 27 or 28 March 2007) , Philippe Gillet, ''ENS Info'' 70, April 2007. was a French mathematician, a student of Alexander Grothendieck. His research focused on non-abelian cohomology and the theory of . In particular, he authored the book ''Cohomologie non-abélienne'' (Springer, 1971) and proved the theorem that bears his name, which gives a characterization of a Grothendieck topos. From 1969 to 1989, he was a professor at |
Adjoint Functors
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems (i.e., constructions of objects having a certain universal property), such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology. By definition, an adjunction between categories \mathcal and \mathcal is a pair of functors (assumed to be covariant) :F: \mathcal \rightarrow \mathcal and G: \mathcal \rightarrow \mathcal and, for all objects X in \mathcal and Y in \mathcal a bijection between the respective morphism s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel (category Theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra. Intuitively, the kernel of the morphism ''f'' : ''X'' → ''Y'' is the "most general" morphism ''k'' : ''K'' → ''X'' that yields zero when composed with (followed by) ''f''. Note that kernel pairs and difference kernels (also known as binary equalisers) sometimes go by the name "kernel"; while related, these aren't quite the same thing and are not discussed in this article. Definition Let C be a category. In order to define a kernel in the general category-theoretical sense, C needs to have zero morphisms. In that case, if ''f'' : ''X'' → ''Y'' is an arbitrary morphism in C, then a kernel of ''f'' is an equaliser of ''f'' and the zero morphism from ''X'' to ''Y''. In symbols: :ker(''f'') = eq(''f'', 0''XY'') To be more explicit, the following universal pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary areas of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Functor
In mathematics, particularly homological algebra, an exact functor is a functor that preserves short exact sequences. Exact functors are convenient for algebraic calculations because they can be directly applied to presentations of objects. Much of the work in homological algebra is designed to cope with functors that ''fail'' to be exact, but in ways that can still be controlled. Definitions Let P and Q be abelian categories, and let be a covariant additive functor (so that, in particular, ''F''(0) = 0). We say that ''F'' is an exact functor if whenever :0 \to A\ \stackrel \ B\ \stackrel \ C \to 0 is a short exact sequence in P then :0 \to F(A) \ \stackrel \ F(B)\ \stackrel \ F(C) \to 0 is a short exact sequence in Q. (The maps are often omitted and implied, and one says: "if 0→''A''→''B''→''C''→0 is exact, then 0→''F''(''A'')→''F''(''B'')→''F''(''C'')→0 is also exact".) Further, we say that ''F'' is *left-exact if whenever 0→''A''→''B''→' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Localizing Subcategory
In mathematics, Serre and localizing subcategories form important classes of subcategories of an abelian category. Localizing subcategories are certain Serre subcategories. They are strongly linked to the notion of a quotient category. Serre subcategories Let \mathcal be an abelian category. A non-empty full subcategory \mathcal is called a ''Serre subcategory'' (or also a ''dense subcategory''), if for every short exact sequence 0\rightarrow A' \rightarrow A\rightarrow A''\rightarrow 0 in \mathcal the object A is in \mathcal if and only if the objects A' and A'' belong to \mathcal. In words: \mathcal is closed under subobjects, quotient objects and extensions. Each Serre subcategory \mathcal of \mathcal is itself an abelian category, and the inclusion functor \mathcal\to\mathcal is exact. The importance of this notion stems from the fact that kernels of exact functors between abelian categories are Serre subcategories, and that one can build (for locally small \mathcal) the q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Of An Abelian Category
In mathematics, the quotient (also called Serre quotient or Gabriel quotient) of an abelian category \mathcal by a Serre subcategory \mathcal is the abelian category \mathcal/\mathcal which, intuitively, is obtained from \mathcal by ignoring (i.e. treating as zero) all objects from \mathcal. There is a canonical exact functor Q \colon \mathcal \to \mathcal/\mathcal whose kernel is \mathcal B, and \mathcal/\mathcal is in a certain sense the most general abelian category with this property. Forming Serre quotients of abelian categories is thus formally akin to forming quotients of groups. Serre quotients are somewhat similar to quotient categories, the difference being that with Serre quotients all involved categories are abelian and all functors are exact. Serre quotients also often have the character of localizations of categories, especially if the Serre subcategory is localizing. Definition Formally, \mathcal A/\mathcal B is the category whose objects are those of \mathca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Full And Faithful Functors
In category theory, a faithful functor is a functor that is injective on hom-sets, and a full functor is surjective on hom-sets. A functor that has both properties is called a full and faithful functor. Formal definitions Explicitly, let ''C'' and ''D'' be (locally small) categories and let ''F'' : ''C'' → ''D'' be a functor from ''C'' to ''D''. The functor ''F'' induces a function :F_\colon\mathrm_(X,Y)\rightarrow\mathrm_(F(X),F(Y)) for every pair of objects ''X'' and ''Y'' in ''C''. The functor ''F'' is said to be *faithful if ''F''''X'',''Y'' is injectiveJacobson (2009), p. 22 *full if ''F''''X'',''Y'' is surjectiveMac Lane (1971), p. 14 *fully faithful (= full and faithful) if ''F''''X'',''Y'' is bijective for each ''X'' and ''Y'' in ''C''. A mnemonic for remembering the term "full" is that the image of the function fills the codomain; a mnemonic for remembering the term "faithful" is that you can trust (have faith) that F(X)=F(Y) implies X=Y. Properties A faithful functor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Of Categories
In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation. If a category is equivalent to the opposite (or dual) of another category then one speaks of a duality of categories, and says that the two categories are dually equivalent. An equivalence of categories consists of a functor between the involved categories, which is required t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Localizing Subcategory
In mathematics, Serre and localizing subcategories form important classes of subcategories of an abelian category. Localizing subcategories are certain Serre subcategories. They are strongly linked to the notion of a quotient category. Serre subcategories Let \mathcal be an abelian category. A non-empty full subcategory \mathcal is called a ''Serre subcategory'' (or also a ''dense subcategory''), if for every short exact sequence 0\rightarrow A' \rightarrow A\rightarrow A''\rightarrow 0 in \mathcal the object A is in \mathcal if and only if the objects A' and A'' belong to \mathcal. In words: \mathcal is closed under subobjects, quotient objects and extensions. Each Serre subcategory \mathcal of \mathcal is itself an abelian category, and the inclusion functor \mathcal\to\mathcal is exact. The importance of this notion stems from the fact that kernels of exact functors between abelian categories are Serre subcategories, and that one can build (for locally small \mathcal) the q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality. A category is formed by two sorts of objects: the objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. One often says that a morphism is an ''arrow'' that ''maps'' its source to its target. Morphisms can be ''composed'' if the target of the first morphism equals the source of the second one, and morphism compos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |