|
Gauss–Kuzmin Distribution
In mathematics, the Gauss–Kuzmin distribution is a discrete probability distribution that arises as the limit probability distribution of the coefficients in the continued fraction expansion of a random variable uniform distribution (continuous), uniformly distributed in (0, 1). The distribution is named after Carl Friedrich Gauss, who derived it around 1800, and Rodion Kuzmin, who gave a bound on the rate of convergence in 1929. It is given by the probability mass function : p(k) = - \log_2 \left( 1 - \frac\right)~. Gauss–Kuzmin theorem Let : x = \cfrac be the continued fraction expansion of a random number ''x'' uniformly distributed in (0, 1). Then : \lim_ \mathbb \left\ = - \log_2\left(1 - \frac\right)~. Equivalently, let : x_n = \cfrac~; then : \Delta_n(s) = \mathbb \left\ - \log_2(1+s) tends to zero as ''n'' tends to infinity. Rate of convergence In 1928, Kuzmin gave the bound : , \Delta_n(s), \leq C \exp(-\alpha \sqrt)~. In 1929, Paul L� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rodion Kuzmin
Rodion Osievich Kuzmin (russian: Родион Осиевич Кузьмин, 9 November 1891, Riabye village in the Haradok district – 24 March 1949, Leningrad) was a Soviet mathematician, known for his works in number theory and analysis. His name is sometimes transliterated as Kusmin. He was an Invited Speaker of the ICM in 1928 in Bologna. Selected results * In 1928, Kuzmin solved the following problem due to Gauss (see Gauss–Kuzmin distribution): if ''x'' is a random number chosen uniformly in (0, 1), and :: x = \frac :is its continued fraction expansion, find a bound for :: \Delta_n(s) = \mathbb \left\ - \log_2(1+s), :where :: x_n = \frac . :Gauss showed that ''Δ''''n'' tends to zero as ''n'' goes to infinity, however, he was unable to give an explicit bound. Kuzmin showed that :: , \Delta_n(s), \leq C e^~, :where ''C'',''α'' > 0 are numerical constants. In 1929, the bound was improved to ''C'' 0.7''n'' by Paul Lévy. * In 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lévy's Constant
In mathematics Lévy's constant (sometimes known as the Khinchin–Lévy constant) occurs in an expression for the asymptotic behaviour of the denominators of the convergents of continued fractions. In 1935, the Soviet mathematician Aleksandr Khinchin showed that the denominators ''q''''n'' of the convergents of the continued fraction expansions of almost all real numbers satisfy :\lim_^= e^ Soon afterward, in 1936, the French mathematician Paul Lévy found eference given in Dover bookP. Levy, ''Théorie de l'addition des variables aléatoires'', Paris, 1937, p. 320. the explicit expression for the constant, namely :e^ = e^ = 3.275822918721811159787681882\ldots The term "Lévy's constant" is sometimes used to refer to \pi^2/(12\ln2) (the logarithm of the above expression), which is approximately equal to 1.1865691104… The value derives from the asymptotic expectation of the logarithm of the ratio of successive denominators, using the Gauss-Kuzmin distribution. In particu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
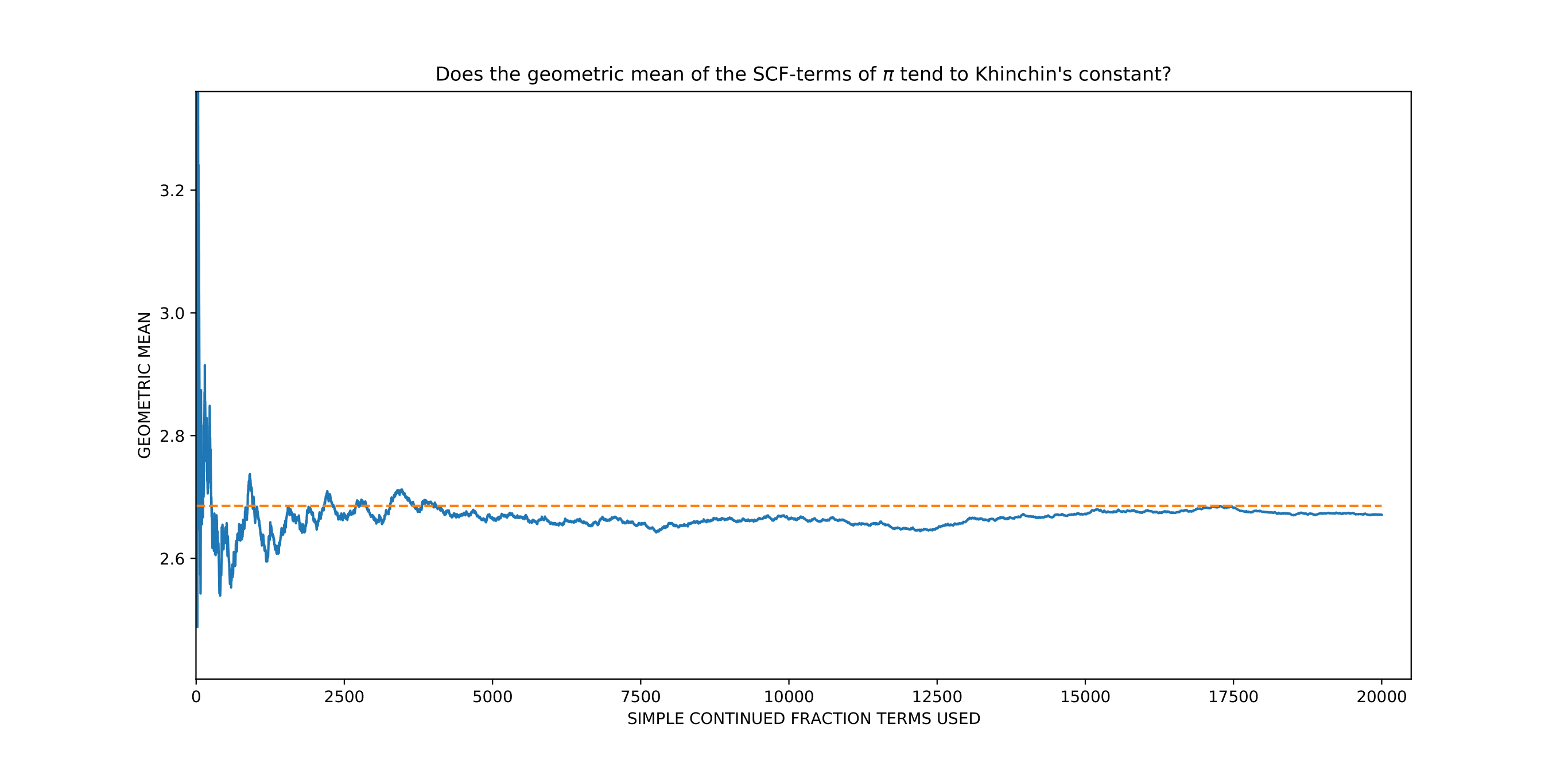
Khinchin's Constant
In number theory, Aleksandr Yakovlevich Khinchin proved that for almost all real numbers ''x'', coefficients ''a''''i'' of the continued fraction expansion of ''x'' have a finite geometric mean that is independent of the value of ''x'' and is known as Khinchin's constant. That is, for :x = a_0+\cfrac\; it is almost always true that :\lim_ \left( a_1 a_2 ... a_n \right) ^ = K_0 where K_0 is Khinchin's constant :K_0 = \prod_^\infty ^ \approx 2.6854520010\dots (with \prod denoting the product over all sequence terms). Although almost all numbers satisfy this property, it has not been proven for ''any'' real number ''not'' specifically constructed for the purpose. Among the numbers whose continued fraction expansions apparently do have this property (based on numerical evidence) are π, the Euler-Mascheroni constant γ, Apéry's constant ζ(3), and Khinchin's constant itself. However, this is unproven. Among the numbers ''x'' whose continued fraction expansions are known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eduard Wirsing
Eduard Wirsing (28 June 1931 – 22 March 2022) was a German mathematician, specializing in number theory. Biography Wirsing was born on 28 June 1931 in Berlin. Wirsing studied at the University of Göttingen and the Free University of Berlin, where he received his doctorate in 1957 under the supervision of Hans-Heinrich Ostmann with thesis ''Über wesentliche Komponenten in der additiven Zahlentheorie'' (On Essential Components in Additive Number Theory). In 1967/68 he was a professor at Cornell University and from 1969 a full professor at the University of Marburg, where he was since 1965. In 1970/71 he was at the Institute for Advanced Study. Since 1974 he was a professor at the University of Ulm, where he led the 1976 Mathematical Colloquium. He retired as professor emeritus in 1999, but continued to be mathematically active. Wirsing organized conferences on analytical number theory at the Oberwolfach Research Institute for Mathematics. In his spare time he played go and ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulletin De La Société Mathématique De France
'' Bulletin de la Société Mathématique de France'' is a mathematics journal published quarterly by Société Mathématique de France. Founded in 1873, the journal publishes articles on mathematics. It publishes articles in French and English. The journal is indexed by ''Mathematical Reviews'' and Zentralblatt MATH. Its 2009 MCQ was 0.58, and its 2009 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as i ... was 0.400. External links * Mathematics journals Publications established in 1873 Multilingual journals Société Mathématique de France academic journals Quarterly journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Lévy (mathematician)
Paul Pierre Lévy (15 September 1886 – 15 December 1971) was a French mathematician who was active especially in probability theory, introducing fundamental concepts such as local time, stable distributions and characteristic functions. Lévy processes, Lévy flights, Lévy measures, Lévy's constant, the Lévy distribution, the Lévy area, the Lévy arcsine law, and the fractal Lévy C curve are named after him. Biography Lévy was born in Paris to a Jewish family which already included several mathematicians. His father Lucien Lévy was an examiner at the École Polytechnique. Lévy attended the École Polytechnique and published his first paper in 1905, at the age of nineteen, while still an undergraduate, in which he introduced the Lévy–Steinitz theorem. His teacher and advisor was Jacques Hadamard. After graduation, he spent a year in military service and then studied for three years at the École des Mines, where he became a professor in 1913. During Worl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Mass Function
In probability and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value. Sometimes it is also known as the discrete density function. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete. A probability mass function differs from a probability density function (PDF) in that the latter is associated with continuous rather than discrete random variables. A PDF must be integrated over an interval to yield a probability. The value of the random variable having the largest probability mass is called the mode. Formal definition Probability mass function is the probability distribution of a discrete random variable, and provides the possible values and their associated probabilities. It is the function p: \R \to ,1/math> defined by for -\inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). Ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions. The distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, ''a'' and ''b'', which are the minimum and maximum values. The interval can either be closed (e.g. , b or open (e.g. (a, b)). Therefore, the distribution is often abbreviated ''U'' (''a'', ''b''), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable ''X'' under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is: : f(x)=\begin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |