|
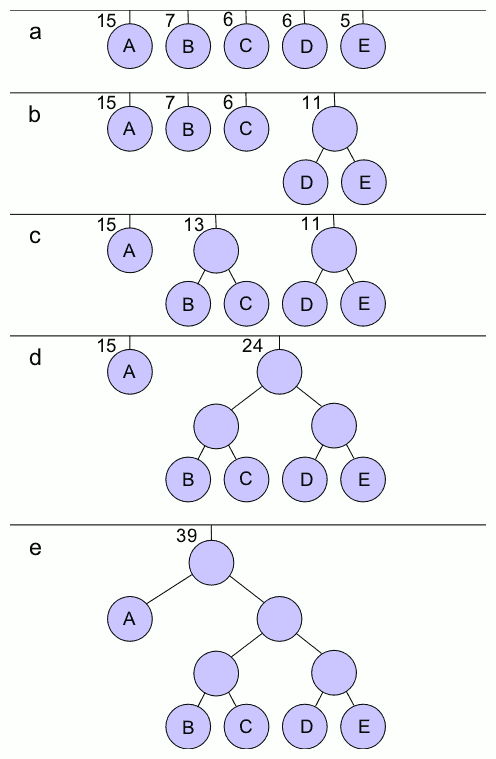
Garsia–Wachs Algorithm
The Garsia–Wachs algorithm is an efficient method for computers to construct optimal binary search trees and Huffman coding, alphabetic Huffman codes, in linearithmic time. It is named after Adriano Garsia and Michelle L. Wachs. Problem description The input to the problem, for an integer n, consists of a sequence of n+1 non-negative weights w_0,w_1,\dots, w_n. The output is a rooted binary tree with n internal nodes, each having exactly two children. Such a tree has exactly n+1 leaf nodes, which can be identified (in the order given by the binary tree) with the n+1 input weights. The goal of the problem is to find a tree, among all of the possible trees with n internal nodes, that minimizes the weighted sum of the ''external path lengths''. These path lengths are the numbers of steps from the root to each leaf. They are multiplied by the weight of the leaf and then summed to give the quality of the overall tree. This problem can be interpreted as a problem of constructing a binar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Binary Search Tree
In computer science, an optimal binary search tree (Optimal BST), sometimes called a weight-balanced binary tree, is a binary search tree which provides the smallest possible search time (or Expected value, expected search time) for a given sequence of accesses (or access probabilities). Optimal BSTs are generally divided into two types: static and dynamic. In the static optimality problem, the tree cannot be modified after it has been constructed. In this case, there exists some particular layout of the nodes of the tree which provides the smallest expected search time for the given access probabilities. Various algorithms exist to construct or approximate the statically optimal tree given the information on the access probabilities of the elements. In the dynamic optimality problem, the tree can be modified at any time, typically by permitting tree rotations. The tree is considered to have a cursor starting at the root which it can move or use to perform modifications. In this c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sentinel Value
In computer programming, a sentinel value (also referred to as a flag value, trip value, rogue value, signal value, or dummy data) is a special value in the context of an algorithm which uses its presence as a condition of termination, typically in a loop or recursive algorithm. The sentinel value is a form of in-band data that makes it possible to detect the end of the data when no out-of-band data (such as an explicit size indication) is provided. The value should be selected in such a way that it is guaranteed to be distinct from all legal data values since otherwise, the presence of such values would prematurely signal the end of the data (the semipredicate problem). A sentinel value is sometimes known as an " Elephant in Cairo", due to a joke where this is used as a physical sentinel. In safe languages, most sentinel values could be replaced with option types, which enforce explicit handling of the exceptional case. Examples Some examples of common sentinel values and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Trees
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theory is that a binary tree is a triple , where ''L'' and ''R'' are binary trees or the empty set and ''S'' is a singleton (a single–element set) containing the root. From a graph theory perspective, binary trees as defined here are arborescences. A binary tree may thus be also called a bifurcating arborescence, a term which appears in some early programming books before the modern computer science terminology prevailed. It is also possible to interpret a binary tree as an undirected, rather than directed graph, in which case a binary tree is an ordered, rooted tree. Some authors use rooted binary tree instead of ''binary tree'' to emphasize the fact that the tree is rooted, but as defined above, a binary tree is always rooted. In math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Algorithms
An algorithm is fundamentally a set of rules or defined procedures that is typically designed and used to solve a specific problem or a broad set of problems. Broadly, algorithms define process(es), sets of rules, or methodologies that are to be followed in calculations, data processing, data mining, pattern recognition, automated reasoning or other problem-solving operations. With the increasing automation of services, more and more decisions are being made by algorithms. Some general examples are; risk assessments, anticipatory policing, and pattern recognition technology. The following is a list of well-known algorithms. Automated planning Combinatorial algorithms General combinatorial algorithms * Brent's algorithm: finds a cycle in function value iterations using only two iterators * Floyd's cycle-finding algorithm: finds a cycle in function value iterations * Gale–Shapley algorithm: solves the stable matching problem * Pseudorandom number generators (uniformly dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Art Of Computer Programming
''The Art of Computer Programming'' (''TAOCP'') is a comprehensive multi-volume monograph written by the computer scientist Donald Knuth presenting programming algorithms and their analysis. it consists of published volumes 1, 2, 3, 4A, and 4B, with more expected to be released in the future. The Volumes 1–5 are intended to represent the central core of computer programming for sequential machines; the subjects of Volumes 6 and 7 are important but more specialized. When Knuth began the project in 1962, he originally conceived of it as a single book with twelve chapters. The first three volumes of what was then expected to be a seven-volume set were published in 1968, 1969, and 1973. Work began in earnest on Volume 4 in 1973, but was suspended in 1977 for work on typesetting prompted by the second edition of Volume 2. Writing of the final copy of Volume 4A began in longhand in 2001, and the first online pre-fascicle, 2A, appeared later in 2001. The first published installment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIAM Journal On Computing
The ''SIAM Journal on Computing'' is a scientific journal focusing on the mathematical and formal aspects of computer science. It is published by the Society for Industrial and Applied Mathematics (SIAM). Although its official ISO abbreviation is ''SIAM J. Comput.'', its publisher and contributors frequently use the shorter abbreviation ''SICOMP''. SICOMP typically hosts the special issues of the IEEE Annual Symposium on Foundations of Computer Science (FOCS) and the Annual ACM Symposium on Theory of Computing (STOC), where about 15% of papers published in FOCS and STOC each year are invited to these special issues. For example, Volume 48 contains 11 out of 85 papers published in FOCS 2016. References External linksSIAM Journal on Computing on |
Alan Tucker
Alan Curtiss Tucker is an American mathematician. He is a professor of applied mathematics at Stony Brook University, and the author of a widely used textbook on combinatorics; he has also made research contributions to graph theory and coding theory. He has had four children, Katie, Lisa, Edward, and James. Education and career Alan Tucker was born on July 6, 1943. He is the son of Princeton mathematician Albert W. Tucker, who fostered the development of game theory in the mid-20th century – his students included John Nash and two other Economics Nobel Laureates. Alan earned a B.A. from Harvard University in 1965 and a Ph.D. in mathematics from Stanford University in 1969.Curriculum vitae retrieved 2014-10-07. He joined the Department of Applied Mathematics and Statistics at |
Sequential Search
In computer science, linear search or sequential search is a method for finding an element within a list. It sequentially checks each element of the list until a match is found or the whole list has been searched. A linear search runs in linear time in the worst case, and makes at most comparisons, where is the length of the list. If each element is equally likely to be searched, then linear search has an average case of comparisons, but the average case can be affected if the search probabilities for each element vary. Linear search is rarely practical because other search algorithms and schemes, such as the binary search algorithm and hash tables, allow significantly faster searching for all but short lists. Algorithm A linear search sequentially checks each element of the list until it finds an element that matches the target value. If the algorithm reaches the end of the list, the search terminates unsuccessfully. Basic algorithm Given a list of elements with values o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array. Binary search runs in Time complexity#Logarithmic time, logarithmic time in the Best, worst and average case, worst case, making O(\log n) comparisons, where n is the number of elements in the array. Binary search is faster than linear search except for small arrays. However, the array must be sorted first to be able to apply binary search. There are specialized data structures designed fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-balancing Binary Search Tree
In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height (maximal number of levels below the root) small in the face of arbitrary item insertions and deletions.Donald Knuth. '' The Art of Computer Programming'', Volume 3: ''Sorting and Searching'', Second Edition. Addison-Wesley, 1998. . Section 6.2.3: Balanced Trees, pp.458–481. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing". For height-balanced binary trees, the height is defined to be logarithmic O(\log n) in the number n of items. This is the case for many binary search trees, such as AVL trees and red–black trees. Splay trees and treaps are self-balancing but not height-balanced, as their height is not guaranteed to be logarithmic in the number of items. Self-bal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Garsia–Wachs Algorithm
The Garsia–Wachs algorithm is an efficient method for computers to construct optimal binary search trees and Huffman coding, alphabetic Huffman codes, in linearithmic time. It is named after Adriano Garsia and Michelle L. Wachs. Problem description The input to the problem, for an integer n, consists of a sequence of n+1 non-negative weights w_0,w_1,\dots, w_n. The output is a rooted binary tree with n internal nodes, each having exactly two children. Such a tree has exactly n+1 leaf nodes, which can be identified (in the order given by the binary tree) with the n+1 input weights. The goal of the problem is to find a tree, among all of the possible trees with n internal nodes, that minimizes the weighted sum of the ''external path lengths''. These path lengths are the numbers of steps from the root to each leaf. They are multiplied by the weight of the leaf and then summed to give the quality of the overall tree. This problem can be interpreted as a problem of constructing a binar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Huffman Coding
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Doctor of Science, Sc.D. student at Massachusetts Institute of Technology, MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The output from Huffman's algorithm can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). The algorithm derives this table from the estimated probability or frequency of occurrence (''weight'') for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in time linear time, linear to the number of input weigh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |