|
Galves–Löcherbach Model
The Galves–Löcherbach model (or GL model) is a mathematical model for a network of neurons with intrinsic stochasticity. In the most general definition, a GL network consists of a countable number of elements (idealized ''neurons'') that interact by sporadic nearly-instantaneous discrete events (''spikes'' or ''firings''). At each moment, each neuron ''N'' fires independently, with a probability that depends on the history of the firings of all neurons since the last time ''N'' last fired. Thus each neuron "forgets" all previous spikes, including its own, whenever it fires. This property is a defining feature of the GL model. In specific versions of the GL model, the past network spike history since the last firing of a neuron ''N'' may be summarized by an internal variable, the ''potential'' of that neuron, that is a weighted sum of those spikes. The potential may include the spikes of only a finite subset of other neurons, thus modeling arbitrary synapse topologies. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
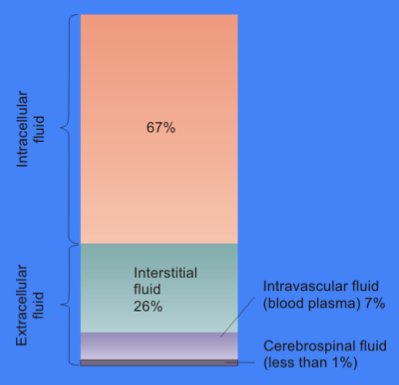
Extracellular Medium
In cell biology, extracellular fluid (ECF) denotes all body fluid outside the cells of any multicellular organism. Total body water in healthy adults is about 60% (range 45 to 75%) of total body weight; women and the obese typically have a lower percentage than lean men. Extracellular fluid makes up about one-third of body fluid, the remaining two-thirds is intracellular fluid within cells. The main component of the extracellular fluid is the interstitial fluid that surrounds cells. Extracellular fluid is the internal environment of all multicellular animals, and in those animals with a blood circulatory system, a proportion of this fluid is blood plasma. Plasma and interstitial fluid are the two components that make up at least 97% of the ECF. Lymph makes up a small percentage of the interstitial fluid. The remaining small portion of the ECF includes the transcellular fluid (about 2.5%). The ECF can also be seen as having two components – plasma and lymph as a delivery system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hodgkin–Huxley Model
The Hodgkin–Huxley model, or conductance-based model, is a mathematical model that describes how action potentials in neurons are initiated and propagated. It is a set of nonlinear differential equations that approximates the electrical characteristics of excitable cells such as neurons and muscle cells. It is a continuous-time dynamical system. Alan Hodgkin and Andrew Huxley described the model in 1952 to explain the ionic mechanisms underlying the initiation and propagation of action potentials in the squid giant axon. They received the 1963 Nobel Prize in Physiology or Medicine for this work. Basic components The typical Hodgkin–Huxley model treats each component of an excitable cell as an electrical element (as shown in the figure). The lipid bilayer is represented as a capacitance (Cm). Voltage-gated ion channels are represented by electrical conductances (''g''''n'', where ''n'' is the specific ion channel) that depend on both voltage and time. Leak channels are rep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biological Neuron Model
Biological neuron models, also known as a spiking neuron models, are mathematical descriptions of the properties of certain cells in the nervous system that generate sharp electrical potentials across their cell membrane, roughly one millisecond in duration, called action potentials or spikes (Fig. 2). Since spikes are transmitted along the axon and synapses from the sending neuron to many other neurons, spiking neurons are considered to be a major information processing unit of the nervous system. Spiking neuron models can be divided into different categories: the most detailed mathematical models are biophysical neuron models (also called Hodgkin-Huxley models) that describe the membrane voltage as a function of the input current and the activation of ion channels. Mathematically simpler are integrate-and-fire models that describe the membrane voltage as a function of the input current and predict the spike times without a description of the biophysical processes that shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NeuroMat
The Research, Innovation, and Dissemination Center for Neuromathematics (RIDC NeuroMat, or simply NeuroMat) is a Brazilian research center established in 2013 at the University of São Paulo that is dedicated to integrating mathematical modeling and theoretical neuroscience. Among the core missions of NeuroMat are the creation of a new mathematical system to understanding neural data and the development of neuroscientific open-source computational tools, keeping an active role under the context of open knowledge, open science and scientific dissemination. The research center is headed by Antonio Galves, from USP's Institute of Mathematics and Statistics, and is funded by the São Paulo Research Foundation (FAPESP). As of 2019, the co-principal investigators are Oswaldo Baffa Filho (USP), Pablo A. Ferrari (USP/UBA), Fernando da Paixão (UNICAMP), Antonio Carlos Roque (USP), Jorge Stolfi (UNICAMP), and Cláudia D. Vargas (UFRJ). Ernst W. Hamburger (USP) was the former director ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrodynamic
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bruno Cessac
Bruno may refer to: People and fictional characters * Bruno (name), including lists of people and fictional characters with either the given name or surname * Bruno, Duke of Saxony (died 880) * Bruno the Great (925–965), Archbishop of Cologne, Duke of Lotharingia and saint * Bruno (bishop of Verden) (920–976), German Roman Catholic bishop * Pope Gregory V (c. 972–999), born Bruno of Carinthia * Bruno of Querfurt (c. 974–1009), Christian missionary bishop, martyr and saint * Bruno of Augsburg (c. 992–1029), Bishop of Augsburg * Bruno (bishop of Würzburg) (1005–1045), German Roman Catholic bishop * Pope Leo IX (1002–1054), born Bruno of Egisheim-Dagsburg * Bruno II (1024–1057), Frisian count or margrave * Bruno the Saxon (fl. 2nd half of the 11th century), historian * Saint Bruno of Cologne (d. 1101), founder of the Carthusians * Bruno (bishop of Segni) (c. 1045–1123), Italian Roman Catholic bishop and saint * Bruno (archbishop of Trier) (died 1124), Ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Chain With Memory Of Variable Length
Stochastic chains with memory of variable length are a family of stochastic chains of finite order in a finite alphabet, such as, for every time pass, only one finite suffix of the past, called context, is necessary to predict the next symbol. These models were introduced in the information theory literature by Jorma Rissanen in 1983, as a universal tool to data compression, but recently have been used to model data in different areas such as biology, linguistics and music. Definition A stochastic chain with memory of variable length is a stochastic chain (X_n)_, taking values in a finite alphabet A, and characterized by a probabilistic context tree (\tau,p), so that *\tau is the group of all contexts. A context X_,\ldots,X_, being l the size of the context, is a finite portion of the past X_,\ldots,X_, which is relevant to predict the next symbol X_; *p is a family of transition probabilities associated with each context. History The class of stochastic chains with memo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jorma Rissanen
Jorma Johannes Rissanen (October 20, 1932 – May 9, 2020) was an information theorist, known for originating the minimum description length (MDL) principle and practical approaches to arithmetic coding for lossless data compression. His work inspired the development of the theory of stochastic chains with memory of variable length. Education and career Rissanen was born in Pielisjärvi (now Lieksa in Finland and grew up in Kemi, a border town between Finland and Sweden. He moved to Helsinki and studied at the Helsinki University of Technology, where he obtained his Master’s degree in electrical engineering in 1956 and licentiate in control theory in 1960. He studied there under Olli Lokki and Hans Blomberg. Rissanen became an IBM researcher since 1960, first in Stockholm, Sweden, while still a Ph.D. student under Hans Blomberg. Most of his PhD work was done remotely as a result and he received his Ph.D. from the Helsinki University of Technology in 1965 with a topic on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interacting Particle System
In probability theory, an interacting particle system (IPS) is a stochastic process (X(t))_ on some configuration space \Omega= S^G given by a site space, a countable-infinite graph G and a local state space, a compact metric space S . More precisely IPS are continuous-time Markov jump processes describing the collective behavior of stochastically interacting components. IPS are the continuous-time analogue of stochastic cellular automata. Among the main examples are the voter model, the contact process, the asymmetric simple exclusion process (ASEP), the Glauber dynamics and in particular the stochastic Ising model. IPS are usually defined via their Markov generator giving rise to a unique Markov process using Markov semigroups and the Hille-Yosida theorem. The generator again is given via so-called transition rates c_\Lambda(\eta,\xi)>0 where \Lambda\subset G is a finite set of sites and \eta,\xi\in\Omega with \eta_i=\xi_i for all i\notin\Lambda. The rates describe ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frank Spitzer
Frank Ludvig Spitzer (July 24, 1926 – February 1, 1992) was an Austrian-born American mathematician who made fundamental contributions to probability theory, including the theory of random walks, fluctuation theory, percolation theory, the Wiener sausage, and especially the theory of interacting particle systems. Rare among mathematicians, he chose to focus broadly on "phenomena", rather than any one of the many specific theorems that might help to articulate a given phenomenon. His book ''Principles of Random Walk'', first published in 1964, remains a well-cited classic. Spitzer was born into a Jewish family in Vienna, Austria, and by the time he was twelve years old, the Nazi threat in Austria was evident. His parents were able to send him to a summer camp for Jewish children in Sweden, and, as a result, Spitzer spent all of the war years in Sweden. He lived with two Swedish families, learned Swedish, graduated from high school, and for one year attended Teknis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |