|
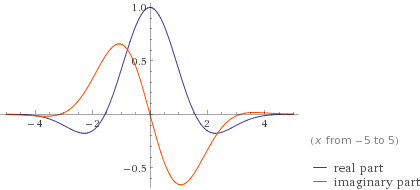
Gabor Wavelet
Gabor wavelets are wavelets invented by Dennis Gabor using complex functions constructed to serve as a basis for Fourier transforms in information theory applications. They are very similar to Morlet wavelets. They are also closely related to Gabor filters. The important property of the wavelet is that it minimizes the product of its standard deviations in the time and frequency domain. Put another way, the uncertainty in information carried by this wavelet is minimized. However they have the downside of being non-orthogonal, so efficient decomposition into the basis is difficult. Since their inception, various applications have appeared, from image processing to analyzing neurons in the human visual system. Minimal uncertainty property The motivation for Gabor wavelets comes from finding some function f(x) which minimizes its standard deviation in the time and frequency domains. More formally, the variance in the position domain is: : (\Delta x)^2 = \frac where f^(x) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing. For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly one tenth of a second. If this wavelet were to be convolved with a signal created from the recording of a melody, then the resulting signal would be useful for determining when the Middle C note appeared in the song. Mathematically, a wavelet correlates with a signal if a portion of the signal is similar. Correlation is at the core of many practical wavelet applications. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including but not limited to au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dennis Gabor
Dennis Gabor ( ; hu, Gábor Dénes, ; 5 June 1900 – 9 February 1979) was a Hungarian-British electrical engineer and physicist, most notable for inventing holography, for which he later received the 1971 Nobel Prize in Physics. He obtained British citizenship in 1934, and spent most of his life in England. Life and career Gabor was born as Günszberg Dénes, into a Jewish family in Budapest, Hungary. In 1918, his family converted to Lutheranism. Dennis was the first-born son of Günszberg Bernát and Jakobovits Adél. Despite having a religious background, religion played a minor role in his later life and he considered himself agnostic. In 1902, the family received permission to change their surname from Günszberg to Gábor. He served with the Hungarian artillery in northern Italy during World War I. He began his studies in engineering at the Technical University of Budapest in 1918, later in Germany, at the Charlottenburg Technical University in Berlin, now known as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering. A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a die (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy. Important sub-fields of information theory include s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morlet Wavelet
In mathematics, the Morlet wavelet (or Gabor wavelet)0). The parameter \sigma in the Morlet wavelet allows trade between time and frequency resolutions. Conventionally, the restriction \sigma>5 is used to avoid problems with the Morlet wavelet at low \sigma (high temporal resolution). For signals containing only slowly varying frequency and amplitude modulations (audio, for example) it is not necessary to use small values of \sigma. In this case, \kappa_ becomes very small (e.g. \sigma>5 \quad \Rightarrow \quad \kappa_5, the frequency of the Morlet wavelet is conventionally taken to be \omega_\simeq\sigma. The wavelet exists as a complex version or a purely real-valued version. Some distinguish between the "real Morlet" vs the "complex Morlet". Others consider the complex version to be the "Gabor wavelet", while the real-valued version is the "Morlet wavelet". Uses Use in medicine In magnetic resonance spectroscopy imaging, the Morlet wavelet transform method offers an i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gabor Filter
In image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for texture analysis, which essentially means that it analyzes whether there is any specific frequency content in the image in specific directions in a localized region around the point or region of analysis. Frequency and orientation representations of Gabor filters are claimed by many contemporary vision scientists to be similar to those of the human visual system. They have been found to be particularly appropriate for texture representation and discrimination. In the spatial domain, a 2-D Gabor filter is a Gaussian kernel function modulated by a sinusoidal plane wave (see Gabor transform). Some authors claim that simple cells in the visual cortex of mammalian brains can be modeled by Gabor functions. Thus, image analysis with Gabor filters is thought by some to be similar to perception in the human visual system. Definition Its impulse response is defined by a sinusoidal wave (a pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg's Uncertainty Principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, ''x'', and momentum, ''p'', can be predicted from initial conditions. Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified. Introduced first in 1927 by the German physicist Werner ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Number
In the physical sciences, the wavenumber (also wave number or repetency) is the ''spatial frequency'' of a wave, measured in cycles per unit distance (ordinary wavenumber) or radians per unit distance (angular wavenumber). It is analogous to temporal frequency, which is defined as the number of wave cycles per unit time (''ordinary frequency'') or radians per unit time (''angular frequency''). In multidimensional systems, the wavenumber is the magnitude of the ''wave vector''. The space of wave vectors is called '' reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics of wave scattering, such as X-ray diffraction, neutron diffraction, electron diffraction, and elementary particle physics. For quantum mechanical waves, the wavenumber multiplied by the reduced Planck's constant is the '' canonical momentum''. Wavenumber can be used to specify quantities other than spatial frequency. For example, in optical spectroscopy, it is often ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
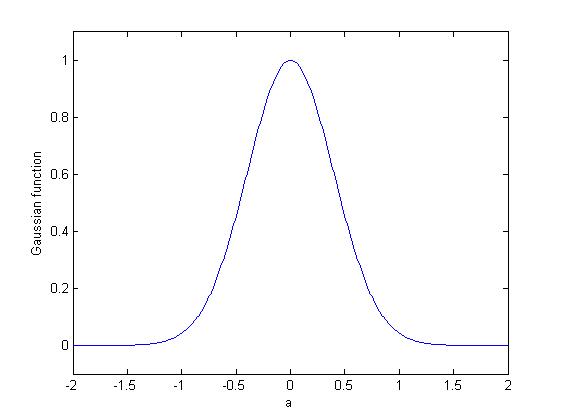
Gabor Transform
The Gabor transform, named after Dennis Gabor, is a special case of the short-time Fourier transform. It is used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time. The function to be transformed is first multiplied by a Gaussian function, which can be regarded as a window function, and the resulting function is then transformed with a Fourier transform to derive the time-frequency analysis.E. Sejdić, I. Djurović, J. Jiang, “Time-frequency feature representation using energy concentration: An overview of recent advances,” ''Digital Signal Processing'', vol. 19, no. 1, pp. 153-183, January 2009. The window function means that the signal near the time being analyzed will have higher weight. The Gabor transform of a signal ''x''(''t'') is defined by this formula: : G_x(\tau,\omega) = \int_^\infty x(t)e^e^\,dt The Gaussian function has infinite range and it is impractical for implementation. However, a level of signi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |