|
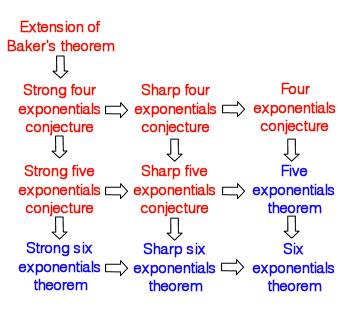
Four Exponentials Conjecture
In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function. Statement If ''x''1, ''x''2 and ''y''1, ''y''2 are two pairs of complex numbers, with each pair being linearly independent over the rational numbers, then at least one of the following four numbers is transcendental: :e^, e^, e^, e^. An alternative way of stating the conjecture in terms of logarithms is the following. For 1 ≤ ''i'', ''j'' ≤ 2 let λ''ij'' be complex numbers such that exp(λ''ij'') are all algebraic. Suppose λ11 and λ12 are linearly independent over the rational numbers, and λ11 and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Ludwig Siegel
Carl Ludwig Siegel (31 December 1896 – 4 April 1981) was a German mathematician specialising in analytic number theory. He is known for, amongst other things, his contributions to the Thue–Siegel–Roth theorem in Diophantine approximation, Siegel's method, Siegel's lemma and the Siegel mass formula for quadratic forms. He was named as one of the most important mathematicians of the 20th century.Pérez, R. A. (2011''A brief but historic article of Siegel'' NAMS 58(4), 558–566. André Weil, without hesitation, named Siegel as the greatest mathematician of the first half of the 20th century. Atle Selberg said of Siegel and his work: Biography Siegel was born in Berlin, where he enrolled at the Humboldt University in Berlin in 1915 as a student in mathematics, astronomy, and physics. Amongst his teachers were Max Planck and Ferdinand Georg Frobenius, whose influence made the young Siegel abandon astronomy and turn towards number theory instead. His best-known student was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Srinivasa Ramanujan
Srinivasa Ramanujan (; born Srinivasa Ramanujan Aiyangar, ; 22 December 188726 April 1920) was an Indian mathematician. Though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable. Ramanujan initially developed his own mathematical research in isolation: according to Hans Eysenck: "He tried to interest the leading professional mathematicians in his work, but failed for the most part. What he had to show them was too novel, too unfamiliar, and additionally presented in unusual ways; they could not be bothered". Seeking mathematicians who could better understand his work, in 1913 he began a postal correspondence with the English mathematician G. H. Hardy at the University of Cambridge, England. Recognising Ramanujan's work as extraordinary, Hardy arranged for him to travel to Cambridge. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Colossally Abundant Number
In mathematics, a colossally abundant number (sometimes abbreviated as CA) is a natural number that, in a particular, rigorous sense, has many divisors. Formally, a number ''n'' is said to be colossally abundant if there is an ε > 0 such that for all ''k'' > 1, :\frac\geq\frac where ''σ'' denotes the sum-of-divisors function. All colossally abundant numbers are also superabundant numbers, but the converse is not true. The first 15 colossally abundant numbers, 2, 6, 12, 60, 120, 360, 2520, 5040, 55440, 720720, 1441440, 4324320, 21621600, 367567200, 6983776800 are also the first 15 superior highly composite numbers, but neither set is a subset of the other. History Colossally abundant numbers were first studied by Ramanujan and his findings were intended to be included in his 1915 paper on highly composite numbers. Unfortunately, the publisher of the journal to which Ramanujan submitted his work, the London Mathematical Society, was in fina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which alway ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gelfond–Schneider Theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. History It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider. Statement : If ''a'' and ''b'' are complex algebraic numbers with ''a'' ≠ 0, 1, and ''b'' not rational, then any value of ''ab'' is a transcendental number. Comments * The values of ''a'' and ''b'' are not restricted to real numbers; complex numbers are allowed (here complex numbers are not regarded as rational when they have an imaginary part not equal to 0, even if both the real and imaginary parts are rational). * In general, is multivalued, where ln stands for the natural logarithm. This accounts for the phrase "any value of" in the theorem's statement. * An equivalent formulation of the theorem is the following: if ''α'' and ''γ'' are nonzero algebraic numbers, and we take any non-zero logarithm of ''α'', then is either rational or transcendental. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E (mathematical Constant)
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of the natural logarithms. It is the limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the area under the curve between and , in which case is the value of for which this area equals one (see image). There are various other characteri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Identity
In mathematics, Euler's identity (also known as Euler's equation) is the equality e^ + 1 = 0 where : is Euler's number, the base of natural logarithms, : is the imaginary unit, which by definition satisfies , and : is pi, the ratio of the circumference of a circle to its diameter. Euler's identity is named after the Swiss mathematician Leonhard Euler. It is a special case of Euler's formula e^ = \cos x + i\sin x when evaluated for . Euler's identity is considered to be an exemplar of mathematical beauty as it shows a profound connection between the most fundamental numbers in mathematics. In addition, it is directly used in a proof that is transcendental, which implies the impossibility of squaring the circle. Mathematical beauty Euler's identity is often cited as an example of deep mathematical beauty. Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kanakanahalli Ramachandra
Kanakanahalli Ramachandra (18 August 1933 – 17 January 2011) was an Indian mathematician working in both analytic number theory and algebraic number theory. Early career After his father's death at age 13, he had to look for a job. Ramachandra worked as a clerk at the Minerva Mills where Ramachandra's father had also worked. In spite of taking up a job quite remote from mathematics, Ramachandra studied number theory all by himself in his free time; especially the works of Ramanujan. Ramachandra completed his graduation and post graduation from Central College, Bangalore. Later, he worked as a lecturer in BMS College of Engineering. Ramachandra also served a very short stint of only six days as a teacher in the Indian Institute of Science, Bangalore. Ramachandra went to the Tata Institute of Fundamental Research (TIFR), Bombay, for his graduate studies in 1958. He obtained his PhD from University of Mumbai in 1965; his doctorate was guided by K. G. Ramanathan. Later care ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |