|
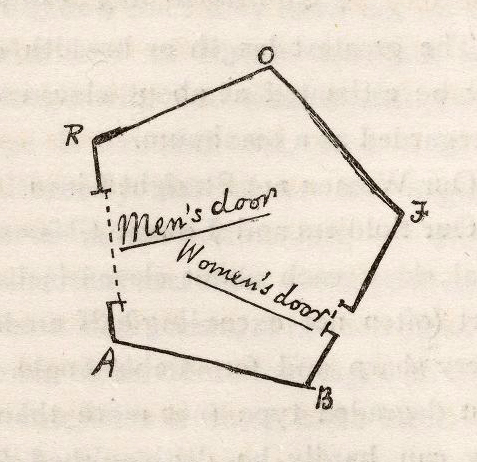
Flatland (1965 Film)
''Flatland: A Romance of Many Dimensions'' is a satirical novella by the English schoolmaster Edwin Abbott Abbott, first published in 1884 by Seeley & Co. of London. Written pseudonymously by "A Square", the book used the fictional two-dimensional world of Flatland to comment on the hierarchy of Victorian culture, but the novella's more enduring contribution is its examination of dimensions. Several films have been made from the story, including the feature film ''Flatland'' (2007). Other efforts have been short or experimental films, including one narrated by Dudley Moore and the short films '' Flatland: The Movie'' (2007) and '' Flatland 2: Sphereland'' (2012). Plot The story describes a two-dimensional world occupied by geometric figures; women are simple line segments, while men are polygons with various numbers of sides. The narrator is a square, a member of the caste of gentlemen and professionals, who guides the readers through some of the implications of life ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edwin A
The name Edwin means "rich friend". It comes from the Old English elements "ead" (rich, blessed) and "ƿine" (friend). The original Anglo-Saxon form is Eadƿine, which is also found for Anglo-Saxon figures. People * Edwin of Northumbria (died 632 or 633), King of Northumbria and Christian saint * Edwin (son of Edward the Elder) (died 933) * Eadwine of Sussex (died 982), King of Sussex * Eadwine of Abingdon (died 990), Abbot of Abingdon * Edwin, Earl of Mercia (died 1071), brother-in-law of Harold Godwinson (Harold II) *Edwin (director) (born 1978), Indonesian filmmaker * Edwin (musician) (born 1968), Canadian musician * Edwin Abeygunasekera, Sri Lankan Sinhala politician, member of the 1st and 2nd State Council of Ceylon * Edwin Ariyadasa (1922-2021), Sri Lankan Sinhala journalist * Edwin Austin Abbey (1852–1911) British artist * Edwin Eugene Aldrin (born 1930), although he changed it to Buzz Aldrin, American astronaut * Edwin Howard Armstrong (1890–1954), American inve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using a line above the symbols for the two endpoints (such as \overline). Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. When the end points both lie on a curve (such as a circle), a line segment is called a chord (geometry), chord (of that curve). In real or complex vector spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proclamation
A proclamation (Lat. ''proclamare'', to make public by announcement) is an official declaration issued by a person of authority to make certain announcements known. Proclamations are currently used within the governing framework of some nations and are usually issued in the name of the head of state. A proclamation is (usually) a non-binding notice. A general distinction is made between official proclamations from states or state organs with a binding character and proclamations from political-social groups or organizations, both of which try to win over the mood of those addressed. In addition, the procedure of proclaiming the beginning of a rule over a certain ruling territory is called a proclamation. For example, on July 26, 1581, the Proclamation of Dutch Independence was signed which led to the creation of the Dutch Republic in 1588, formally recognized in 1648 by the Peace of Münster. The announcement of the intention to marry two people, the bidding, was referred to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apostle
An apostle (), in its literal sense, is an emissary, from Ancient Greek ἀπόστολος (''apóstolos''), literally "one who is sent off", from the verb ἀποστέλλειν (''apostéllein''), "to send off". The purpose of such sending off is usually to convey a message, and thus "messenger" is a common alternative translation; other common translations include "ambassador" and "envoy". The term in Ancient Greek also has other related meanings. The term derives from the Ancient Greek. In Christianity, the term was used in the New Testament for Jesus' Twelve Apostles (including Peter, James, and John), as well as a wider group of early Christian figures, including Paul, Barnabas, and Junia. The term is also used to designate an important missionary of Christianity to a region, e.g. the " apostle of Germany". Some other religions use the term for comparable figures in their history. The word in this sense may be used metaphorically in various contexts, but is mostly found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position (geometry), position of an element (i.e., Point (mathematics), point). This is the informal meaning of the term dimension. In mathematics, a tuple of Real number, numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the -dimensional Euclidean space. When , this space is called three-dimensional Euclidean space (or simply Euclidean space when the context is clear). It serves as a model of the physical universe (when relativity theory is not considered), in which all known matter exists. While this space remains the most compelling and useful way to model the world as it is experienced, it is only one example of a large variety of spaces in three dimensions called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest circle that c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disk (mathematics)
In geometry, a disk (also spelled disc). is the region in a plane bounded by a circle. A disk is said to be ''closed'' if it contains the circle that constitutes its boundary, and ''open'' if it does not. For a radius, r, an open disk is usually denoted as D_r and a closed disk is \overline. However in the field of topology the closed disk is usually denoted as D^2 while the open disk is \operatorname D^2. Formulas In Cartesian coordinates, the ''open disk'' of center (a, b) and radius ''R'' is given by the formula :D=\ while the ''closed disk'' of the same center and radius is given by :\overline=\. The area of a closed or open disk of radius ''R'' is π''R''2 (see area of a disk). Properties The disk has circular symmetry. The open disk and the closed disk are not topologically equivalent (that is, they are not homeomorphic), as they have different topological properties from each other. For instance, every closed disk is compact whereas every open disk is not compact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monarch
A monarch is a head of stateWebster's II New College DictionarMonarch Houghton Mifflin. Boston. 2001. p. 707. Life tenure, for life or until abdication, and therefore the head of state of a monarchy. A monarch may exercise the highest authority and power in the Sovereign state, state, or others may wield that power on behalf of the monarch. Usually a monarch either personally inheritance, inherits the lawful right to exercise the state's sovereign rights (often referred to as ''the throne'' or ''the Crown, the crown'') or is elective monarchy, selected by an established process from a family or cohort eligible to provide the nation's monarch. Alternatively, an individual may self-proclaimed monarchy, proclaim themself monarch, which may be backed and Legitimacy (political), legitimated through acclamation, right of conquest or a combination of means. If a young child is crowned the monarch, then a regent is often appointed to govern until the monarch reaches the requisite adult a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point (geometry)
In classical Euclidean geometry, a point is a primitive notion that models an exact location in space, and has no length, width, or thickness. In modern mathematics, a point refers more generally to an element of some set called a space. Being a primitive notion means that a point cannot be defined in terms of previously defined objects. That is, a point is defined only by some properties, called axioms, that it must satisfy; for example, ''"there is exactly one line that passes through two different points"''. Points in Euclidean geometry Points, considered within the framework of Euclidean geometry, are one of the most fundamental objects. Euclid originally defined the point as "that which has no part". In two-dimensional Euclidean space, a point is represented by an ordered pair (, ) of numbers, where the first number conventionally represents the horizontal and is often denoted by , and the second number conventionally represents the vertical and is often denoted by . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-dimensional Space
In physics and mathematics, a sequence of ''n'' numbers can specify a location in ''n''-dimensional space. When , the set of all such locations is called a one-dimensional space. An example of a one-dimensional space is the number line, where the position of each point on it can be described by a single number. In algebraic geometry there are several structures that are technically one-dimensional spaces but referred to in other terms. A field ''k'' is a one-dimensional vector space over itself. Similarly, the projective line over ''k'' is a one-dimensional space. In particular, if , the complex numbers, then the complex projective line P1(ℂ) is one-dimensional with respect to ℂ, even though it is also known as the Riemann sphere. More generally, a ring is a length-one module over itself. Similarly, the projective line over a ring is a one-dimensional space over the ring. In case the ring is an algebra over a field, these spaces are one-dimensional with respect to the algebr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |