|
Fick's Law
Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which Fick would become famous. Fick's law is analogous to the relationships discovered at the same epoch by other eminent scientists: Darcy's law (hydraulic flow), Ohm's law (charge transport), and Fourier's Law (heat transport). Fick's experiments (modeled on Graham's) dealt with measuring the concentrations and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardiac Output
In cardiac physiology, cardiac output (CO), also known as heart output and often denoted by the symbols Q, \dot Q, or \dot Q_ , edited by Catherine E. Williamson, Phillip Bennett is the volumetric flow rate of the heart's pumping output: that is, the volume of blood being pumped by both ventricles of the heart, per unit time (usually measured per minute). Cardiac output (CO) is the product of the heart rate (HR), i.e. the number of heartbeats per minute (bpm), and the stroke volume (SV), which is the volume of blood pumped from the left ventricle per beat; thus giving the formula: :CO = HR \times SV Values for cardiac output are usually denoted as L/min. For a healthy individual weighing 70 kg, the cardiac output at rest averages about 5 L/min; assuming a heart rate of 70 beats/min, the stroke volume would be approximately 70 mL. Because cardiac output is related to the quantity of blood delivered to various parts of the body, it is an important component of how effi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Kernel
In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a specified domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some auxiliary importance throughout mathematical physics. The heat kernel represents the evolution of temperature in a region whose boundary is held fixed at a particular temperature (typically zero), such that an initial unit of heat energy is placed at a point at time ''t'' = 0. ] The most well-known heat kernel is the heat kernel of ''d''-dimensional Euclidean space R''d'', which has the form of a time-varying Gaussian function, :K(t,x,y) = \exp\left(t\Delta\right)(x,y) = \frac e^\qquad(x,y\in\mathbb^d,t>0)\, This solves the heat equation :\frac(t,x,y) = \Delta_x K(t,x,y)\, for all ''t'' > 0 and ''x'',''y'' ∈ R''d'', where Δ is the Laplace operator, with the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Solution
In mathematics, a fundamental solution for a linear partial differential operator is a formulation in the language of distribution theory of the older idea of a Green's function (although unlike Green's functions, fundamental solutions do not address boundary conditions). In terms of the Dirac delta "function" , a fundamental solution is a solution of the inhomogeneous equation Here is ''a priori'' only assumed to be a distribution. This concept has long been utilized for the Laplacian in two and three dimensions. It was investigated for all dimensions for the Laplacian by Marcel Riesz. The existence of a fundamental solution for any operator with constant coefficients — the most important case, directly linked to the possibility of using convolution to solve an arbitrary right hand side — was shown by Bernard Malgrange and Leon Ehrenpreis. In the context of functional analysis, fundamental solutions are usually developed via the Fredholm alternative and explored ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Equation
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. As the prototypical parabolic partial differential equation, the heat equation is among the most widely studied topics in pure mathematics, and its analysis is regarded as fundamental to the broader field of partial differential equations. The heat equation can also be considered on Riemannian manifolds, leading to many geometric applications. Following work of Subbaramiah Minakshisundaram and Åke Pleijel, the heat equation is closely related with spectral geometry. A seminal nonlinear variant of the heat equation was introduced to differential geometry by James Eells and Joseph Sampson in 1964, inspiring the introduction of the Ricci flow by Richard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplacian
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the nabla operator), or \Delta. In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian of a function at a point measures by how much the average value of over small spheres or balls centered at deviates from . The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics: the Laplacian of the gravitational potential due to a given mass density distribution is a constant multiple of that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Theory Of Gases
Kinetic (Ancient Greek: κίνησις “kinesis”, movement or to move) may refer to: * Kinetic theory, describing a gas as particles in random motion * Kinetic energy In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its a ..., the energy of an object that it possesses due to its motion Art and entertainment * Kinetic art, a form of art involving mechanical and/or random movement, including optical illusions. * ''Kinetic'', the 13th episode of the first season of the TV series ''Smallville'' * ''Kinetic'' (comics), a comic by Allan Heinberg and Kelley Pucklett * "Kinetic" (song), a song by Radiohead Companies * Kinetic Engineering Limited, Indian automotive manufacturer * Kinetic Group, Australian-based public transport company Technology * "Kinetic", Seiko's trademark for its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of subs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
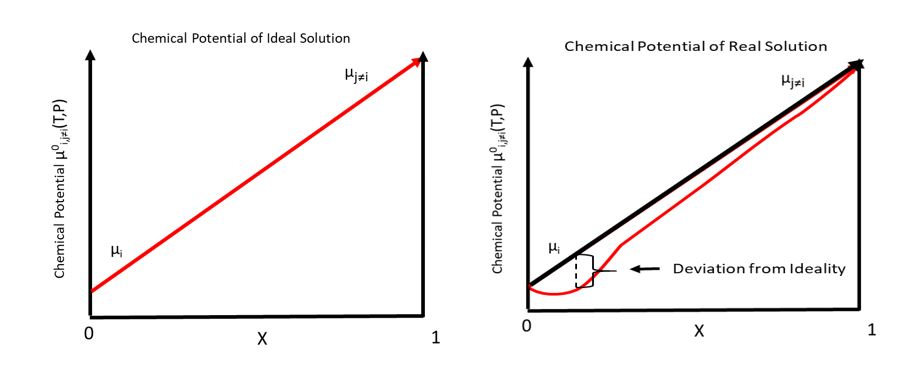
Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically, density is defined as mass divided by volume: : \rho = \frac where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight. For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure. To simplify comparisons of density across different syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molar Mass
In chemistry, the molar mass of a chemical compound is defined as the mass of a sample of that compound divided by the amount of substance which is the number of moles in that sample, measured in moles. The molar mass is a bulk, not molecular, property of a substance. The molar mass is an ''average'' of many instances of the compound, which often vary in mass due to the presence of isotopes. Most commonly, the molar mass is computed from the standard atomic weights and is thus a terrestrial average and a function of the relative abundance of the isotopes of the constituent atoms on Earth. The molar mass is appropriate for converting between the mass of a substance and the amount of a substance for bulk quantities. The molecular mass and formula mass are commonly used as a synonym of molar mass, particularly for molecular compounds; however, the most authoritative sources define it differently. The difference is that molecular mass is the mass of one specific particle or m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |