|
Five-qubit Error Correcting Code
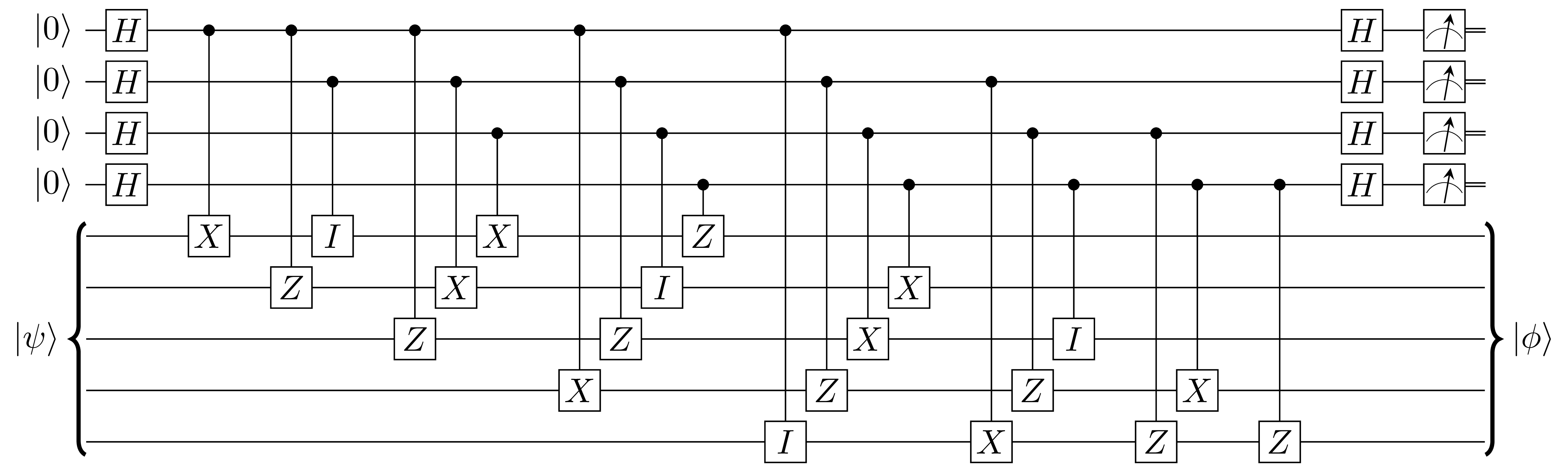
The five-qubit error correcting code or the 5,1,3 code, is the smallest quantum error correction, quantum error correcting code that can protect a Physical and logical qubits, logical qubit from any arbitrary single qubit error. In this code, 5 Physical and logical qubits, physical qubits are used to encode the logical qubit. With X and Z being Pauli matrices and I the Identity matrix, this code's Stabilizer code#Definition, generators are \langle XZZXI, IXZZX, XIXZZ,ZXIXZ \rangle. Its logical operators are \bar = XXXXX and \bar = ZZZZZ. Once the logical qubit is encoded, errors on the physical qubits can be detected via stabilizer measurements. A lookup table that maps the results of the stabilizer measurements to the types and locations of the errors gives the control system of the quantum computer enough information to correct errors. History Peter Shor original quantum error correcting code of 1995, used 9 qubits. The five-qubit error correcting code was published indepen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Five Qubit Code Stabilizer Measurement Circuit
5 (five) is a number, numeral (linguistics), numeral and numerical digit, digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. Humans, and many other animals, have 5 Digit (anatomy), digits on their Limb (anatomy), limbs. Mathematics 5 is a Fermat prime, a Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length of the hypotenuse of the smallest integer-sided right triangle, making part of the smallest Pythagorean triple (3, 4, 5). 5 is the first safe prime and the first good prime. 11 forms the first pair of sexy primes with 5. 5 is the second Fermat number, Fermat prime, of a total of five known Fermat primes. 5 is also the first of three known Wilson primes (5, 13, 563). Geometry A shape with five sides is called a pentagon. The pentagon is the first regular polygon that does not Tessellation, tile the Plane (geometry), plane with copies of itself. It is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wojciech H
Wojciech () is a Polish name, equivalent to Czech Vojtěch , Slovak Vojtech, and German Woitke. The name is formed from two Slavic roots: * ''wój'' (Slavic: ''voj''), a root pertaining to war. It also forms words like ''wojownik'' ("warrior") and ''wojna'' ("war"). * ''ciech'' (from an earlier form, ''tech''), meaning "joy". The resulting combination means "he who enjoys war" or "joyous warrior". Its Polish diminutive forms include ''Wojtek'' , ''Wojtuś'' , ''Wojtas'', ''Wojcio'', ''Wojteczek'', ''Wojcieszek'', ''Wojtaszka'', ''Wojtaszek'', ''Wojan'' (noted already in 1136), ''Wojko'', and variants noted as early as 1400, including ''Woytko'', ''Woythko'', and ''Voytko''. The feminine form is Wojciecha (). Related names in South Slavic languages include ''Vojko'', ''Vojislav'', and ''Vojteh''. The name has been rendered into German in several different variations, including: ''Woitke'', ''Witke'', ''Voitke'', ''Voytke'', ''Woytke'', ''Vogtke'', ''Woytegk'', ''Woytek'', ''Wogtk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Complete Set Of Commuting Observables
In quantum mechanics, a complete set of commuting observables (CSCO) is a set of commuting operators whose common eigenvectors can be used as a basis to express any quantum state. In the case of operators with discrete spectra, a CSCO is a set of commuting observables whose simultaneous eigenspaces span the Hilbert space and are linearly independent, so that the eigenvectors are uniquely specified by the corresponding sets of eigenvalues. In some simple cases, like bound state problems in one dimension, the energy spectrum is nondegenerate, and energy can be used to uniquely label the eigenstates. In more complicated problems, the energy spectrum is degenerate, and additional observables are needed to distinguish between the eigenstates. Since each pair of observables in the set commutes, the observables are all compatible so that the measurement of one observable has no effect on the result of measuring another observable in the set. It is therefore ''not'' necessary to specify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Controlled NOT Gate
In computer science, the controlled NOT gate (also C-NOT or CNOT), controlled-''X'' gate, controlled-bit-flip gate, Feynman gate or controlled Pauli-X is a quantum logic gate that is an essential component in the construction of a gate-based quantum computer. It can be used to entangle and disentangle Bell states. Any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit rotations. The gate is sometimes named after Richard Feynman who developed an early notation for quantum gate diagrams in 1986. The CNOT can be expressed in the Pauli basis as: : \mbox = e^= e^. Being both unitary and Hermitian, CNOT has the property e^=(\cos \theta)I+(i\sin \theta) U and U =e^=e^, and is involutory. The CNOT gate can be further decomposed as products of rotation operator gates and exactly one two qubit interaction gate, for example : \mbox =e^R_(-\pi/2)R_(-\pi/2)R_(-\pi/2)R_(\pi/2)R_(\pi/2). In general, any sing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Parity Measurement
Parity measurement (also referred to as Operator measurement) is a procedure in quantum information science used for error detection in quantum qubits. A parity measurement checks the equality of two qubits to return a true or false answer, which can be used to determine whether a correction needs to occur.Steane, Andrew M. (2006). A tutorial on quantum error correction. ''Quantum Computers, Algorithms and Chaos'', 1-32. https://www2.physics.ox.ac.uk/sites/default/files/ErrorCorrectionSteane06.pdf Additional measurements can be made for a system greater than two qubits. Because parity measurement does not measure the state of singular bits but rather gets information about the whole state, it is considered an example of a joint measurement. Joint measurements do not have the consequence of destroying the original state of a qubit as normal quantum measurements do. Mathematically speaking, parity measurements are used to project a state into an eigenstate of an operator and to acquire ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
William Wootters
William "Bill" Kent Wootters is an American theoretical physicist, and one of the founders of the field of quantum information theory. In a 1982 joint paper with Wojciech H. Zurek, Wootters proved the no-cloning theorem, at the same time as Dennis Dieks, and independently of James L. Park who had formulated the no-cloning theorem in 1970. He is known for his contributions to the theory of quantum entanglement including quantitative measures of it, entanglement-assisted communication (notably quantum teleportation, discovered by Wootters and collaborators in 1993) and entanglement distillation. The term ''qubit,'' denoting the basic unit of quantum information, originated in a conversation between Wootters and Benjamin Schumacher in 1992. He earned a B.S. from Stanford University in 1973, and his Ph.D. from the University of Texas at Austin in 1980. His thesis was titled ''The Acquisition of Information from Quantum Measurements,'' and Linda Reichl was his doctoral advisor, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
John A
Sir John Alexander Macdonald (10 or 11January 18156June 1891) was the first prime minister of Canada, serving from 1867 to 1873 and from 1878 until his death in 1891. He was the Fathers of Confederation, dominant figure of Canadian Confederation, and had a political career that spanned almost half a century. Macdonald was born in Scotland; when he was a boy his family immigrated to Kingston, Ontario, Kingston in the Province of Upper Canada (today in eastern Ontario). As a lawyer, he was involved in several high-profile cases and quickly became prominent in Kingston, which elected him in 1844 to the legislature of the Province of Canada. By 1857, he had become List of Joint Premiers of the Province of Canada, premier under the colony's unstable political system. In 1864, when no party proved capable of governing for long, he agreed to a proposal from his political rival, George Brown (Canadian politician), George Brown, that the parties unite in a Great Coalition to seek fede ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
David DiVincenzo
David P. DiVincenzo (born 1959) is an American theoretical physicist. He is the director of the Institute of Theoretical Nanoelectronics at the Peter Grünberg Institute at the Forschungszentrum Jülich and professor at the Institute for Quantum Information at RWTH Aachen University. With Daniel Loss (at the University of Basel), he proposed the Loss–DiVincenzo quantum computer in 1997, which would use electron spins in quantum dots as qubits. Career In 1996, during his research at IBM, he published a paper "Topics in Quantum Computing" which outlined the five minimal requirements he predicted were necessary for creating a quantum computer. It has since become known as the " DiVincenzo criteria" and has influenced much of the experimental research into developing a working quantum computer. The DiVincenzo criteria that a quantum computer implementation must satisfy are as follows: # A scalable physical system with well-characterized qubits, # The ability to initialize the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Charles H
Charles is a masculine given name predominantly found in English and French speaking countries. It is from the French form ''Charles'' of the Proto-Germanic name (in runic alphabet) or ''*karilaz'' (in Latin alphabet), whose meaning was "free man". The Old English descendant of this word was '' Ċearl'' or ''Ċeorl'', as the name of King Cearl of Mercia, that disappeared after the Norman conquest of England. The name was notably borne by Charlemagne (Charles the Great), and was at the time Latinized as ''Karolus'' (as in ''Vita Karoli Magni''), later also as '' Carolus''. Etymology The name's etymology is a Common Germanic noun ''*karilaz'' meaning "free man", which survives in English as churl (James (wikt:Appendix:Proto-Indo-European/ǵerh₂-">ĝer-, where the ĝ is a palatal consonant, meaning "to rub; to be old; grain." An old man has been worn away and is now grey with age. In some Slavic languages, the name ''Drago (given name), Drago'' (and variants: ''Drago ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Juan Pablo Paz
Juan Pablo Paz (born 1959) is an Argentinian physicist who works in the field of quantum computing. A research scientist currently working at the University of Buenos Aires, he has also worked at the Los Alamos National Laboratory in the United States. Biography Juan Pablo Paz was born in Buenos Aires in 1959. He studied at the University of Buenos Aires, where he got his Master (1984) and Ph.D. (1988) degrees. He then went for postdoctoral stays to the University of Maryland (1989-1991) and the Los Alamos National Laboratory (1991-1994). In 1994 he became associate professor in the Physics Department of the University of Buenos Aires and in 1999 associate professor. From 2003 to 2004 he was member of the technical staff at Los Alamos. Currently he is full professor in the Physics Department of the University of Buenos Aires, where he leads the ''Quantum Foundations and Information'' group. Between 1984 and 2004 he was married to Silvina Ponce Dawson (who is also a physicist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |