|
Fermi Resonance
A Fermi resonance is the shifting of the energies and intensities of absorption bands in an infrared or Raman spectrum. It is a consequence of quantum mechanical wavefunction mixing. The phenomenon was explained by the Italian physicist Enrico Fermi. Selection rules and occurrence Two conditions must be satisfied for the occurrence of Fermi Resonance: *The two vibrational modes of a molecule transform according to the same irreducible representation in their molecular point group. In other words, the two vibrations must have the same symmetries (Mulliken symbols). *The transitions coincidentally have very similar energies. Fermi resonance most often occurs between fundamental and overtone excitations, if they are nearly coincident in energy. Fermi resonance leads to two effects. First, the high energy mode shifts to higher energy and the low energy mode shifts to still lower energy. Second, the weaker mode gains intensity (becomes more allowed) and the more intense band decreases i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infrared Spectrum
Infrared (IR), sometimes called infrared light, is electromagnetic radiation (EMR) with wavelengths longer than those of visible light. It is therefore invisible to the human eye. IR is generally understood to encompass wavelengths from around 1 millimeter (300 GHz) to the nominal red edge of the visible spectrum, around 700 nanometers (430 THz). Longer IR wavelengths (30 μm-100 μm) are sometimes included as part of the terahertz radiation range. Almost all black-body radiation from objects near room temperature is at infrared wavelengths. As a form of electromagnetic radiation, IR propagates energy and momentum, exerts radiation pressure, and has properties corresponding to both those of a wave and of a particle, the photon. It was long known that fires emit invisible heat; in 1681 the pioneering experimenter Edme Mariotte showed that glass, though transparent to sunlight, obstructed radiant heat. In 1800 the astronomer Sir William Herschel discovered th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raman Spectroscopy
Raman spectroscopy () (named after Indian physicist C. V. Raman) is a spectroscopic technique typically used to determine vibrational modes of molecules, although rotational and other low-frequency modes of systems may also be observed. Raman spectroscopy is commonly used in chemistry to provide a structural fingerprint by which molecules can be identified. Raman spectroscopy relies upon inelastic scattering of photons, known as Raman scattering. A source of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range is used, although X-rays can also be used. The laser light interacts with molecular vibrations, phonons or other excitations in the system, resulting in the energy of the laser photons being shifted up or down. The shift in energy gives information about the vibrational modes in the system. Infrared spectroscopy typically yields similar yet complementary information. Typically, a sample is illuminated with a laser beam. Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enrico Fermi
Enrico Fermi (; 29 September 1901 – 28 November 1954) was an Italian (later naturalized American) physicist and the creator of the world's first nuclear reactor, the Chicago Pile-1. He has been called the "architect of the nuclear age" and the "architect of the atomic bomb". He was one of very few physicists to excel in both theoretical physics and experimental physics. Fermi was awarded the 1938 Nobel Prize in Physics for his work on induced radioactivity by neutron bombardment and for the discovery of transuranium elements. With his colleagues, Fermi filed several patents related to the use of nuclear power, all of which were taken over by the US government. He made significant contributions to the development of statistical mechanics, Quantum mechanics, quantum theory, and nuclear physics, nuclear and particle physics. Fermi's first major contribution involved the field of statistical mechanics. After Wolfgang Pauli formulated his Pauli exclusion principle, exclusion pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Vibration
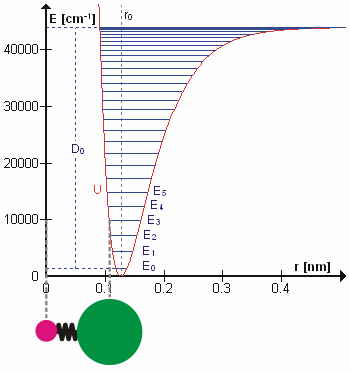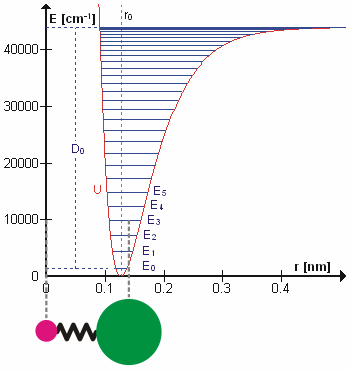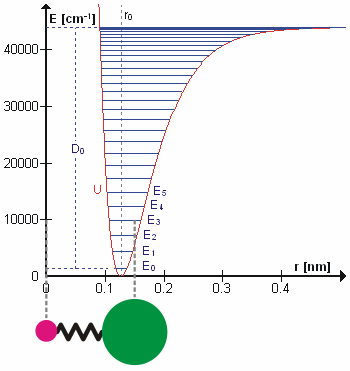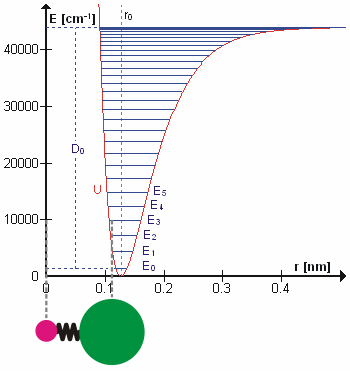
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 µm. For a diatomic molecule A−B, the vibrational frequency in s−1 is given by \nu = \frac \sqrt , where k is the force constant in dyne/cm or erg/cm2 and μ is the reduced mass given by \frac = \frac+\frac. The vibrational wavenumber in cm−1 is \tilde \;= \frac \sqrt, where c is the speed of light in cm/s. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of different parts of the molecule. In general, a non-linear molecule with ''N'' atoms has 3''N'' – 6 normal modes of vibration, but a ''linear'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irreducible Representation
In mathematics, specifically in the representation theory of groups and algebras, an irreducible representation (\rho, V) or irrep of an algebraic structure A is a nonzero representation that has no proper nontrivial subrepresentation (\rho, _W,W), with W \subset V closed under the action of \. Every finite-dimensional unitary representation on a Hilbert space V is the direct sum of irreducible representations. Irreducible representations are always indecomposable (i.e. cannot be decomposed further into a direct sum of representations), but converse may not hold, e.g. the two-dimensional representation of the real numbers acting by upper triangular unipotent matrices is indecomposable but reducible. History Group representation theory was generalized by Richard Brauer from the 1940s to give modular representation theory, in which the matrix operators act on a vector space over a field K of arbitrary characteristic, rather than a vector space over the field of real numbers or o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Symmetry
Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain many of a molecule's chemical properties, such as whether or not it has a dipole moment, as well as its allowed spectroscopic transitions. To do this it is necessary to use group theory. This involves classifying the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Symmetry is useful in the study of molecular orbitals, with applications to the Hückel method, to ligand field theory, and to the Woodward-Hoffmann rules. Many university level textbooks on physical chemistry, quantum chemistry, spectroscopy and inorganic chemistry discuss symmetry. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ketone
In organic chemistry, a ketone is a functional group with the structure R–C(=O)–R', where R and R' can be a variety of carbon-containing substituents. Ketones contain a carbonyl group –C(=O)– (which contains a carbon-oxygen double bond C=O). The simplest ketone is acetone (where R and R' is methyl), with the formula . Many ketones are of great importance in biology and in industry. Examples include many sugars (ketoses), many steroids (e.g., testosterone), and the solvent acetone. Nomenclature and etymology The word ''ketone'' is derived from ''Aketon'', an old German word for ''acetone''. According to the rules of IUPAC nomenclature, ketone names are derived by changing the suffix ''-ane'' of the parent alkane to ''-anone''. Typically, the position of the carbonyl group is denoted by a number, but traditional nonsystematic names are still generally used for the most important ketones, for example acetone and benzophenone. These nonsystematic names are considere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained. Common metho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Chemistry
Computational chemistry is a branch of chemistry that uses computer simulation to assist in solving chemical problems. It uses methods of theoretical chemistry, incorporated into computer programs, to calculate the structures and properties of molecules, groups of molecules, and solids. It is essential because, apart from relatively recent results concerning the hydrogen molecular ion (dihydrogen cation, see references therein for more details), the quantum many-body problem cannot be solved analytically, much less in closed form. While computational results normally complement the information obtained by chemical experiments, it can in some cases predict hitherto unobserved chemical phenomena. It is widely used in the design of new drugs and materials. Examples of such properties are structure (i.e., the expected positions of the constituent atoms), absolute and relative (interaction) energies, electronic charge density distributions, dipoles and higher multipole moments, vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |