|
Fermi Liquid
Fermi liquid theory (also known as Landau's Fermi-liquid theory) is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interactions among the particles of the many-body system do not need to be small. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas (i.e. non-interacting fermions), and why other properties differ. Important examples of where Fermi liquid theory has been successfully applied are most notably electrons in most metals and liquid helium-3. Liquid helium-3 is a Fermi liquid at low temperatures (but not low enough to be in its superfluid phase). Helium-3 is an isotope of helium, with 2 protons, 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. Generally, it has a half-odd-integer spin: spin , spin , etc. In addition, these particles obey the Pauli exclusion principle. Fermions include all quarks and leptons and all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in relativistic quantum field theory, particles with integer spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referred to as the spin-statistics relation is, in fact, a spin statistics-quantum numb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family, and are generally thought to be elementary particles because they have no known components or substructure. The electron's mass is approximately 1/1836 that of the proton. Quantum mechanical properties of the electron include an intrinsic angular momentum ( spin) of a half-integer value, expressed in units of the reduced Planck constant, . Being fermions, no two electrons can occupy the same quantum state, in accordance with the Pauli exclusion principle. Like all elementary particles, electrons exhibit properties of both particles and waves: They can collide with other particles and can be diffracted like light. The wave properties of electrons are easier to observe with experiments than those of other particles like neutrons and protons because electrons have a lower mass and hence a longer de Broglie wavele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle-resolved Photoemission Spectroscopy
Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoelectric effect, in which an incoming photon of sufficient energy ejects an electron from the surface of a material. By directly measuring the kinetic energy and emission angle distributions of the emitted photoelectrons, the technique can map the electronic band structure and Fermi surfaces. ARPES is best suited for the study of one- or two-dimensional materials. It has been used by physicists to investigate high-temperature superconductors, graphene, Topological insulator, topological materials, quantum well states, and materials exhibiting charge density waves. ARPES systems consist of a monochromatic light source to deliver a narrow beam of photons, a sample holder connected to a manipulator used to position the sample of a material, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
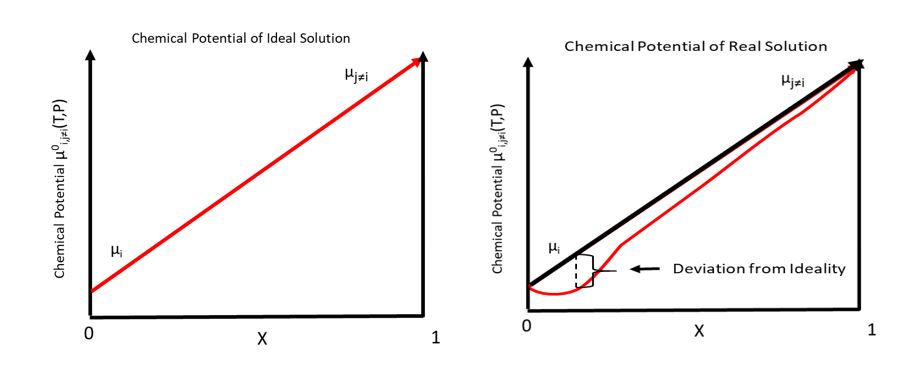
Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Green's Function
In mathematics, a Green's function is the impulse response of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions. This means that if \operatorname is the linear differential operator, then * the Green's function G is the solution of the equation \operatorname G = \delta, where \delta is Dirac's delta function; * the solution of the initial-value problem \operatorname y = f is the convolution (G \ast f). Through the superposition principle, given a linear ordinary differential equation (ODE), \operatorname y = f, one can first solve \operatorname G = \delta_s, for each , and realizing that, since the source is a sum of delta functions, the solution is a sum of Green's functions as well, by linearity of . Green's functions are named after the British mathematician George Green, who first developed the concept in the 1820s. In the modern study of linear partial differential equations, Green's functions are s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature. In a Fermi gas, the lowest occupied state is taken to have zero kinetic energy, whereas in a metal, the lowest occupied state is typically taken to mean the bottom of the conduction band. The term "Fermi energy" is often used to refer to a different yet closely related concept, the Fermi ''level'' (also called electrochemical potential).The use of the term "Fermi energy" as synonymous with Fermi level (a.k.a. electrochemical potential) is widespread in semiconductor physics. For example:''Electronics (fundamentals And Applications)''by D. Chattopadhyay''Semiconductor Physics and Applications''by Balkanski and Wallis. There are a few key differences between the Fermi level and Fermi energy, at least as they are used in this article: * The Fermi energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renormalization
Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian. For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Exclusion Principle
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940. In the case of electrons in atoms, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers: ''n'', the principal quantum number; ', the azimuthal quantum number; ''m'', the magnetic quantum number; and ''ms'', the spin quantum number. For example, if two electrons reside in the same orbital, then their ''n'', ', and ''m'' values are the same; therefore their ''ms'' must be different, and thus the electrons must have opposite half-integer spin projections of 1/2 and −1/2. Particles with an integer spin, or bosons, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuprate Superconductor
Cuprate superconductors are a family of high-temperature superconducting materials made of layers of copper oxides (CuO2) alternating with layers of other metal oxides, which act as charge reservoirs. At ambient pressure, cuprate superconductors are the highest temperature superconductors known. However, the mechanism by which superconductivity occurs is still not understood. History The first cuprate superconductor was found in 1986 in the non-stoichiometric cuprate lanthanum barium copper oxide by IBM researchers Georg Bednorz and Karl Alex Müller. The critical temperature for this material was 35K, well above the previous record of 23 K. The discovery led to a sharp increase in research on the cuprates, resulting in thousands of publications between 1986 and 2001. Bednorz and Müller were awarded the Nobel Prize in Physics in 1987, only a year after their discovery. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
High Temperature Superconductor
High-temperature superconductors (abbreviated high-c or HTS) are defined as materials that behave as superconductors at temperatures above , the boiling point of liquid nitrogen. The adjective "high temperature" is only in respect to previously known superconductors, which function at even colder temperatures close to absolute zero. In absolute terms, these "high temperatures" are still far below ambient, and therefore require cooling. The first high-temperature superconductor was discovered in 1986, by IBM researchers Johannes Georg Bednorz, Bednorz and Karl Alexander Müller, Müller, who were awarded the Nobel Prize in Physics in 1987 "for their important break-through in the discovery of superconductivity in ceramic materials". Most high-c materials are type-II superconductors. The major advantage of high-temperature superconductors is that they can be cooled by using liquid nitrogen, as opposed to the previously known superconductors which require expensive and hard-to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strongly Correlated Material
Strongly correlated materials are a wide class of compounds that include insulators and electronic materials, and show unusual (often technologically useful) electronic and magnetic properties, such as metal-insulator transitions, heavy fermion behavior, half-metallicity, and spin-charge separation. The essential feature that defines these materials is that the behavior of their electrons or spinons cannot be described effectively in terms of non-interacting entities. Theoretical models of the electronic (fermionic) structure of strongly correlated materials must include electronic (fermionic) correlation to be accurate. As of recently, the label quantum materials is also used to refer to strongly correlated materials, among others. Transition metal oxides Many transition metal oxides belong to this class which may be subdivided according to their behavior, ''e.g.'' high-Tc, spintronic materials, multiferroics, Mott insulators, spin Peierls materials, heavy fermion material ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strontium Ruthenate
Strontium ruthenate may refer to two compounds: * Monostrontium ruthenate, SrRuO3, a ferromagnetic perovskite. * Distrontium ruthenate Distrontium ruthenate, also known as strontium ruthenate, is an oxide of strontium and ruthenium with the chemical formula Sr2RuO4. It was the first reported perovskite superconductor that did not contain copper. Strontium ruthenate is struct ..., Sr2RuO4, a perovskite superconductor that does not contain copper. {{set index Strontium compounds Ruthenium(IV) compounds Transition metal oxides ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |