|
Fermi's Golden Rule
In quantum physics, Fermi's golden rule is a formula that describes the transition rate (the probability of a transition per unit time) from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak perturbation. This transition rate is effectively independent of time (so long as the strength of the perturbation is independent of time) and is proportional to the strength of the coupling between the initial and final states of the system (described by the square of the matrix element of the perturbation) as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth. General Although the rule is named after Enrico Fermi, most of the work leading to it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squared Modulus
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations ''x''^2 ( caret) or ''x''**2 may be used in place of ''x''2. The adjective which corresponds to squaring is '' quadratic''. The square of an integer may also be called a square number or a perfect square. In algebra, the operation of squaring is often generalized to polynomials, other expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear polynomial is the quadratic polynomial . One of the important properties of squaring, for numbers as well as in many other mathematical systems, is that (f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Level
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's nucleus. The closest shell to the nucleus is called the " shell" (also called "K shell"), followed by the " shell" (or "L shell"), then the " shell" (or "M shell"), and so on farther and farther from the nucleus. The shells correspond with the principal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scanning Tunneling Microscope
A scanning tunneling microscope (STM) is a type of microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in Physics in 1986. STM senses the surface by using an extremely sharp conducting tip that can distinguish features smaller than 0.1 nm with a 0.01 nm (10 pm) depth resolution. This means that individual atoms can routinely be imaged and manipulated. Most microscopes are built for use in ultra-high vacuum at temperatures approaching zero kelvin, but variants exist for studies in air, water and other environments, and for temperatures over 1000 °C. STM is based on the concept of quantum tunneling. When the tip is brought very near to the surface to be examined, a bias voltage applied between the two allows electrons to tunnel through the vacuum separating them. The resulting ''tunneling current'' is a function of the tip position, app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brillouin Zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. In the same way the Bravais lattice is divided up into Wigner–Seitz cells in the real lattice, the reciprocal lattice is broken up into Brillouin zones. The boundaries of this cell are given by planes related to points on the reciprocal lattice. The importance of the Brillouin zone stems from the description of waves in a periodic medium given by Bloch's theorem, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone. The first Brillouin zone is the locus of points in reciprocal space that are closer to the origin of the reciprocal lattice than they are to any other reciprocal lattice points (see the derivation of the Wigner–Seitz cell). Another definition is as the set of points in ''k''-space that can be reached from the origin without crossing any Bragg plane. Equivalently, this is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Dipole Moment
The transition dipole moment or transition moment, usually denoted \mathbf_ for a transition between an initial state, m, and a final state, n, is the electric dipole moment associated with the transition between the two states. In general the transition dipole moment is a complex vector quantity that includes the phase factors associated with the two states. Its direction gives the polarization of the transition, which determines how the system will interact with an electromagnetic wave of a given polarization, while the square of the magnitude gives the strength of the interaction due to the distribution of charge within the system. The SI unit of the transition dipole moment is the Coulomb-meter (Cm); a more conveniently sized unit is the Debye (D). Definition A single charged particle For a transition where a single charged particle changes state from , \psi_a \rangle to , \psi_b \rangle , the transition dipole moment \text is (\text a \rightarrow b) = \langle \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photoluminescence
Photoluminescence (abbreviated as PL) is light emission from any form of matter after the absorption of photons (electromagnetic radiation). It is one of many forms of luminescence (light emission) and is initiated by photoexcitation (i.e. photons that excite electrons to a higher energy level in an atom), hence the prefix ''photo-''. Following excitation, various relaxation processes typically occur in which other photons are re-radiated. Time periods between absorption and emission may vary: ranging from short femtosecond-regime for emission involving free-carrier plasma in inorganic semiconductorsHayes, G.R.; Deveaud, B. (2002). "Is Luminescence from Quantum Wells Due to Excitons?". ''Physica Status Solidi A'' 190 (3): 637–640doi:10.1002/1521-396X(200204)190:33.0.CO;2-7/ref> up to milliseconds for phosphoresence processes in molecular systems; and under special circumstances delay of emission may even span to minutes or hours. Observation of photoluminescence at a certain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bloch Waves
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential take the form of a plane wave modulated by a periodic function. The theorem is named after the physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written where \mathbf is position, \psi is the wave function, u is a periodic function with the same periodicity as the crystal, the wave vector \mathbf is the crystal momentum vector, e is Euler's number, and i is the imaginary unit. Functions of this form are known as Bloch functions or Bloch states, and serve as a suitable basis for the wave functions or states of electrons in crystalline solids. Named after Swiss physicist Felix Bloch, the description of electrons in terms of Bloch functions, termed Bloch electrons (or less often ''Bloch Waves''), underlies the concept of electronic band structures. These eigenstates are written with subscripts as \psi_, where n is a disc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
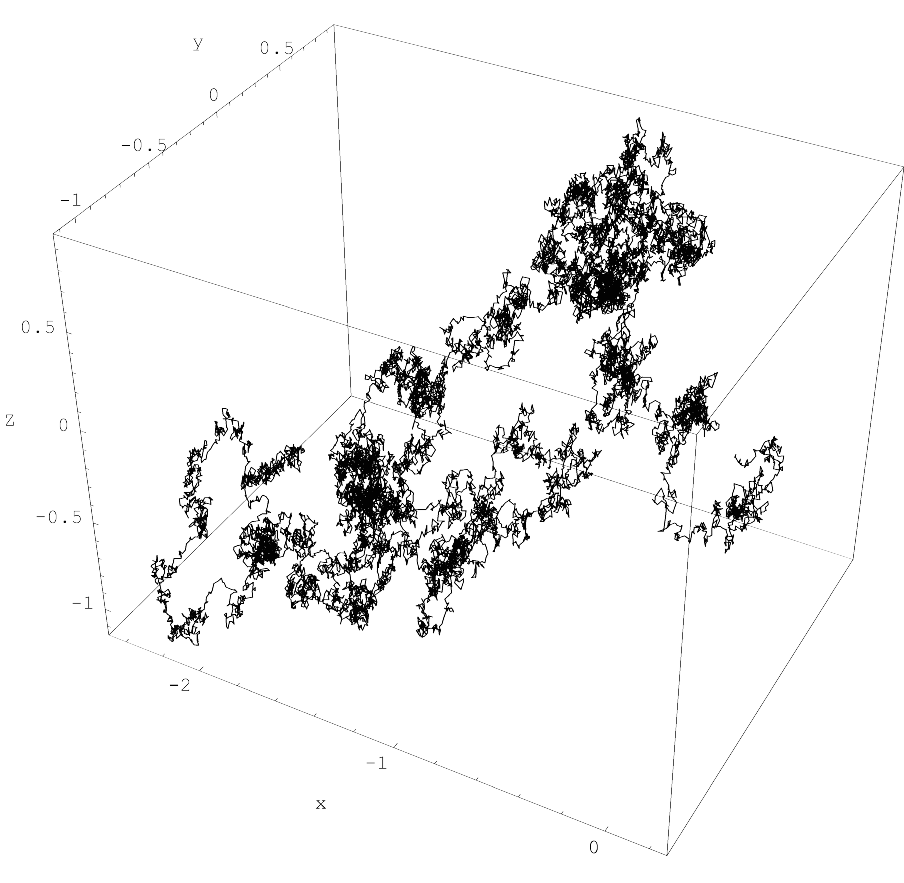
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov assumption is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (conditional on both past and present values) depends only upon the pres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. The current understanding of the unit impulse is as a linear functional that maps every continuous function (e.g., f(x)) to its value at zero of its domain (f(0)), or as the weak limit of a sequence of bump functions (e.g., \delta(x) = \lim_ \frace^), which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta distributions. The delta function was introduced by physicist Paul Dirac as a tool for the normalization of state vectors. It also has uses in probability theory and signal processing. Its validity was disputed until Laurent Schwartz developed the theory of distributions where it is defined as a linear form acting o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Confinement
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy (kinetic energy in the case of a gravitational potential well) because it is captured in the local minimum of a potential well. Therefore, a body may not proceed to the global minimum of potential energy, as it would naturally tend to do due to entropy. Overview Energy may be released from a potential well if sufficient energy is added to the system such that the local maximum is surmounted. In quantum physics, potential energy may escape a potential well without added energy due to the probabilistic characteristics of quantum particles; in these cases a particle may be imagined to tunnel ''through'' the walls of a potential well. The graph of a 2D potential energy function is a potential energy surface that can be imagined as the Earth's surface in a landscape of hills and valleys. Then a potential well would be a va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
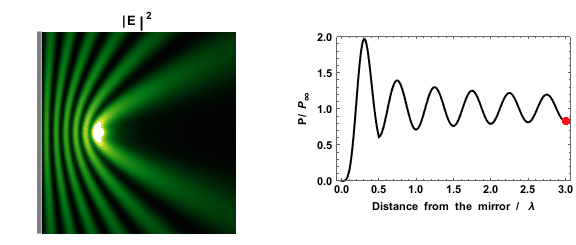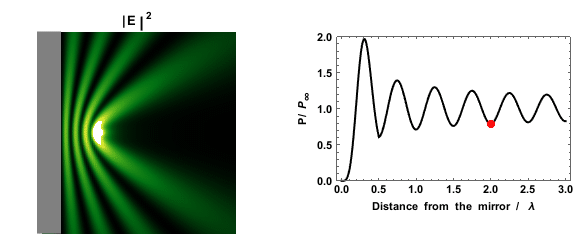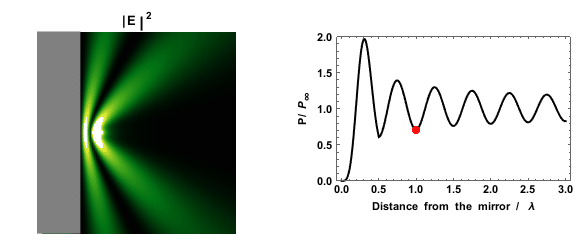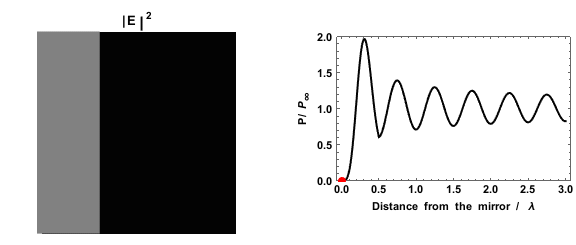

.png)